В статье получен алгоритм решения линейной однородной системы дифференциальных уравнений, который использует жорданову нормальную форму матрицы этой системы и получено классификацию решений такой системы третьего порядка.
Ключевые слова:жорданова нормальная форма, линейные однородные системы дифференциальных уравнений, решения систем дифференциальных уравнений.
ЖНФ имеет широкое применение. Мы рассматриваем использование ЖНФ для классификации решений линейных однородных систем дифференциальных уравнений (ЛОСДУ). Вообще дифференциальные уравнения и методы исследования их решений широко используются в разнообразных отраслях и разделах современной науки и техники. Поэтому исследование дифференциальных уравнений остается актуальным в современной науке.
Данная работа представляет способ классификации решений ЛОСДУ с постоянными коэффициентами с действительной матрицей системы. Этот способ использует классификацию ЖНФ таких матриц.
ЛОСДУ п-го порядка с постоянными коэффициентами можно записать в виде
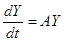 , (1)
, (1)
где 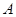 — квадратная матрица п-го порядка,
— квадратная матрица п-го порядка, 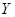 — столбик неизвестных функций
— столбик неизвестных функций 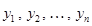 ,
, 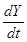 — столбик производных этих функций.
— столбик производных этих функций.
Экспонентой 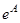 квадратной матрицы
квадратной матрицы 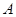 называется матрица
называется матрица 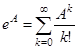 , где
, где 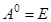 — единичная матрица. Тогда
— единичная матрица. Тогда 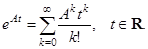 Согласно [1, с.133], система (1) имеет общее решение
Согласно [1, с.133], система (1) имеет общее решение 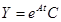 , где
, где 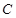 — столбик произвольных коэффициентов.
— столбик произвольных коэффициентов.
По основной теореме, каждая квадратная матрица над алгебраически замкнутым полем (в частности, над 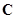 ) приводится к ЖНФ. Т. е., для каждой квадратной матрицы
) приводится к ЖНФ. Т. е., для каждой квадратной матрицы 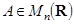 существует такая невырожденная матрица
существует такая невырожденная матрица 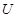 , что
, что 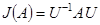 [2]. Существует алгоритм нахождения ЖНФ матрицы
[2]. Существует алгоритм нахождения ЖНФ матрицы 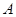 .
.
1. Найти характеристический многочлен матрицы 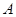 и её собственные значения.
и её собственные значения.
2. Для каждого собственного числа 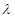 матрицы
матрицы 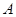 и для каждого
и для каждого 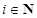 вычислить количество
вычислить количество 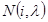 клеток
клеток 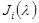 , которые входят в ЖНФ матрицы
, которые входят в ЖНФ матрицы 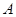 . Для этого вычислить числа
. Для этого вычислить числа 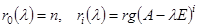 до тех пор, пока не найдется такое
до тех пор, пока не найдется такое 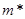 , что
, что 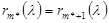 . Потом воспользоваться формулой
. Потом воспользоваться формулой
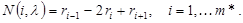
3. Построить ЖНФ 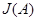 как блочно-диагональную матрицу, диагональ которой составляют клетки Жордана
как блочно-диагональную матрицу, диагональ которой составляют клетки Жордана 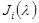 , где
, где 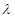 пробегает все собственные значения матрицы
пробегает все собственные значения матрицы 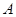 , и каждая из клеток
, и каждая из клеток 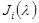 встречается
встречается 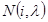 раз. [3]
раз. [3]
Каждой клетке Жордана порядка 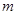 соответствует циклический базис
соответствует циклический базис 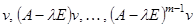 длины
длины 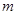 (цепочка длины
(цепочка длины 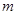 ). Поэтому количество цепочек длины
). Поэтому количество цепочек длины 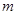 корневого подпространства оператора
корневого подпространства оператора 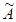 с матрицей
с матрицей 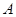 , соответствующих собственному значению
, соответствующих собственному значению 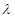 , равно
, равно 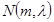 , а объединение всех таких цепочек образует цепочный базис, соответствующий
, а объединение всех таких цепочек образует цепочный базис, соответствующий 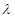 . Алгоритм нахождения такого базиса описано в [3].
. Алгоритм нахождения такого базиса описано в [3].
1. Найти ФСР однородной системы с матрицей 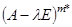 .
.
2. Для каждого вектора 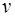 из этой ФСР построить цепочку
из этой ФСР построить цепочку 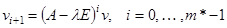 .
.
3. Выбрать 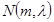 цепочек длины
цепочек длины 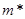 , состоящих из линейно независимых векторов. (Это будет часть искомого базиса.)
, состоящих из линейно независимых векторов. (Это будет часть искомого базиса.)
4. Проделать аналогичные действия со следующим (по убыванию) 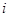 , для которого
, для которого 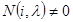 , следя за линейной независимостью полученных векторов с выбранными ранее.
, следя за линейной независимостью полученных векторов с выбранными ранее.
5. Продолжать таким образом, пока не будут выбраны все цепочки.
После нахождения цепочного базиса для каждого собственного числа матрицы 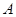 мы можем привести эту матрицу к жордановой форме, но в этом нужно действовать осмотрительно, нумеруя базисные векторы
мы можем привести эту матрицу к жордановой форме, но в этом нужно действовать осмотрительно, нумеруя базисные векторы 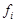 так, как описано в [3]. Искомая матрица
так, как описано в [3]. Искомая матрица 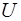 состоит из координат полученных базисных векторов
состоит из координат полученных базисных векторов 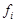 , записанных столбиками.
, записанных столбиками.
Заметим, если действительную матрицу 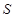 умножить на столбик функций
умножить на столбик функций 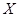 , то получим столбик функций
, то получим столбик функций 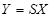 , причем
, причем 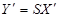 , поскольку
, поскольку
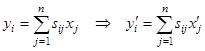 .
.
По рассмотренному выше, 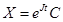 — решение ЛОСДУ
— решение ЛОСДУ 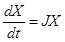 . Пусть
. Пусть 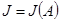 — соответствующая ЖНФ матрицы
— соответствующая ЖНФ матрицы 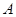 и
и 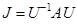 . Тогда
. Тогда 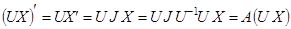 , откуда
, откуда 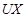 — решение ЛОСДУ
— решение ЛОСДУ 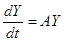 . Значит решение этой системы представляется
. Значит решение этой системы представляется
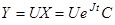 .
.
Этот результат позволяет упростить решение системы 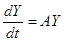 , для чего достаточно воспользоваться следующим алгоритмом:
, для чего достаточно воспользоваться следующим алгоритмом:
1. Найти ЖНФ 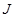 матрицы
матрицы 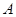 и матрицу
и матрицу 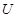 . из столбцов жорданового базиса.
. из столбцов жорданового базиса.
2. Вычислить экспоненту 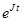 .
.
3. Общее решение системы (1) записать в виде 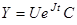 .
.
Также этот результат позволяет классифицировать ЛОСДУ (1) по различным видам решений, используя классификацию соответствующих жордановых матриц. Для примера рассмотрим ЛОСДУ третьего порядка. Жордановы матрицы третьего порядка над полем комплексных чисел по клеточно-диагональному разнообразию имеют шесть видов.
10 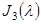 ; 40
; 40 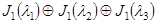 , где
, где 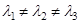 ;
;
20 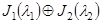 , где
, где 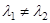 ; 50
; 50 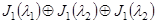 , где
, где 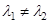 ;
;
30 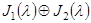 ; 60
; 60 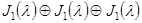 . [4].
. [4].
Если ЖНФ матрицы системы третьего порядка 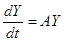 имеет вид
имеет вид
10: 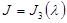 и
и 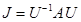 , то
, то 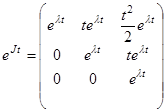 и общее решение этой системы имеет вид
и общее решение этой системы имеет вид
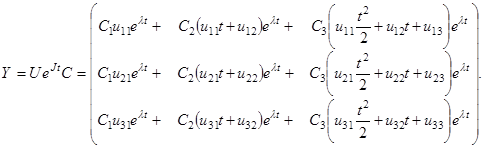
Учитывая, что столбиками матрицы 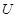 являются векторы жорданового базиса
являются векторы жорданового базиса 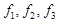 , этот вид будет следующим:
, этот вид будет следующим:
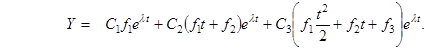
Аналогично, для всех остальных типов жордановых матриц третьего порядка, общие решения ЛОСДУ (1) имеют вид
20 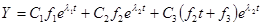 ,
, 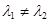 ;
;
30 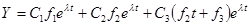 ;
;
40 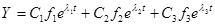 ,
, 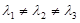 ;
;
50 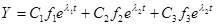 ,
, 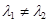 ;
;
60 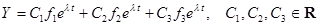 .
.
Следует заметить, что для ЛОСДУ третьего порядка с вещественной матрицей только в случае 40 возможно появление комплексных (причем пары комплексно сопряженных) собственных значений. В этой ситуации можно рассмотреть изменение вида общего решения системы, что не входит в цели данной статьи.
Литература:
1. Арнольд В. И. Обыкновенные дифференциальные уравнения. — М.: Наука, 1982. — 273с.
2. Кострикин А. И. Введение в алгебру. Часть II. Линейная алгебра: учебник для вузов. — 2-е изд., исправл. / — М.: Физико-математическая литература, 2001. — 368 с.
3. Мазорчук В. С. Методичний посібник до теми «Жорданова нормальна форма» для студентів механіко-математичного факультету / — Київ: Київський університет імені Тараса Шевченка, 1998. — 123с.







