В статье изложены условия фазового равновесия «жидкость — пар» в однокомпонентной системе. Для наглядного изображения фазовых превращений использована диаграмма состояния.
Ключевые слова: гетерогенная система, жидкость, однокомпонентная система, пар, фазовое равновесие.
Термодинамическая система, состоящая из различных по физическим или химическим свойствам частей, отделенных друг от друга поверхностями раздела, называется гетерогенной [1, с. 415].
Любая гетерогенная система состоит из нескольких фаз. Фазой называется часть гетерогенной системы, ограниченная поверхностью раздела и характеризующаяся одинаковыми физическими и химическими свойствами.
В однокомпонентных системах фазы состоят из одного вещества в различных агрегатных состояниях — твердом, жидком и газообразном. Равновесие между различными агрегатными состояниями называют фазовым равновесием.
Исследованию фазовых равновесий посвящен ряд публикаций [2, 3] и др.], что указывает на определенный интерес ученых к этой проблеме. Для меня эта тема является важной, актуальной и представляет интерес потому, что она не изучается в школе на уроках химии.
Одним из типов гетерогенного равновесия, которое заканчивается в критической точке, является равновесие «жидкость — пар» (испарение и конденсация) (рис. 1) [4, с. 117].
В жидкостях всегда имеется некоторое число молекул, энергия которых достаточна для преодоления притяжения к другим молекулам и которые способны оторваться от поверхности жидкости и перейти в окружающее их пространство. Этот процесс для жидкости называется испарением (или парообразованием).
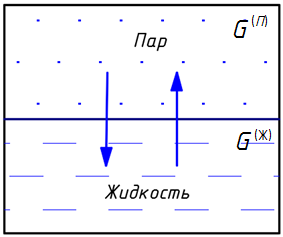
Рис. 1. Система «жидкость — пар»
Испарение жидкости идет при любой температуре, но его интенсивность с повышением температуры возрастает. Наряду с процессом испарения происходит компенсирующий его процесс конденсации пара в жидкость. Если число молекул, покидающих жидкость за единицу времени через единицу поверхности, равно числу молекул, переходящих из пара в жидкость, то наступает динамическое равновесие между процессами испарения и конденсации. Пар, находящийся в равновесии со своей жидкостью, называется насыщенным.
Любая термодинамическая система обладает определенными свойствами. Термодинамические свойства, наименьшее количество которых необходимо для описания состояния данной системы, называются параметрами состояния. Состояние однокомпонентных систем однозначно определяется двумя параметрами, в качестве которых наиболее целесообразно выбирать температуру и давление [5, с. 215].
Заданная системы будет находиться в состоянии равновесия при условиях равенства температур всех фаз, их давлений, а также равенства химических потенциалов каждого компонента в каждой фазе (рис. 2) [6]:
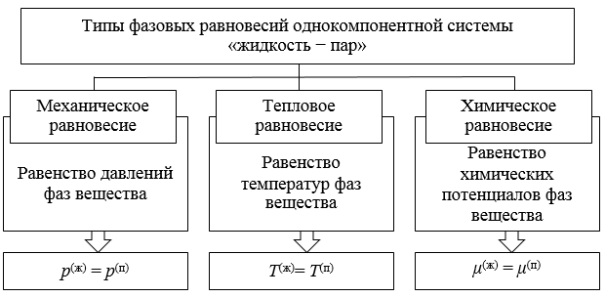
Рис. 2. Условия равновесия однокомпонентной системы «жидкость — пар»
Из анализа условий равновесия (рис. 2) получено правило фаз Гиббса, которое можно сформулировать следующим образом: число степеней свободы ( f ) равновесной гетерогенной системы, на которую влияют только температура ( T ) и давление ( p ), равно числу независимых компонентов системы ( k ) минус число фаз ( Ф ) плюс два. Математически правило фаз Гиббса обычно записывают в виде [7, с. 72]:
f = k — Ф + 2. (1)
Число степеней свободы рассматриваемой двухфазной однокомпонентной системы равно единице ( f = 1–2 + 2). Следовательно, задание постоянного давления определяет температуру сосуществования фаз и наоборот, закрепление температуры сосуществования однозначно определяет давление паров над жидкостью. Для наглядного изображения фазовых превращений в системе «жидкость — пар» используется диаграмма состояния, на которой в координатах p , T задается зависимость между температурой фазового перехода и давлением в виде кривой испарения, разделяющей поле диаграммы на две области, соответствующих условиям существования жидкой и газообразной фаз (рис. 3) [8, с. 174]. Кривая на диаграмме называется кривой фазового равновесия, каждая точка на ней соответствует условию равновесия двух сосуществующих фаз — «жидкости и пара».
Если изменять давление на диаграмме p , Т вдоль линии ВD , пересекая кривую равновесия в точке С , то при пересечении кривой равновесия будет происходить переход вещества из одной фазы в другую.
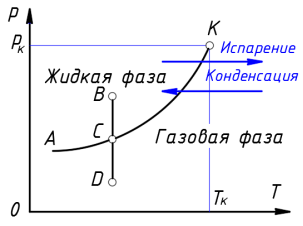
Рис. 3. Диаграмма состояния однокомпонентной системы «жидкость — пар»
Кривая испарения АК заканчивается в точке К . Эта конечная точка фазового равновесия «жидкость — пар» называется критической точкой. Температура и давление, соответствующие этой точке, получили название критической температуры Т к и критического давления р к .
При критической температуре двухфазная система переходит в однофазную. Поэтому выше критической температуры может существовать только однофазная система. Переход двухфазной системы в однофазную при критической температуре происходит без поглощения теплоты и изменения удельного объема.
Фазовое равновесие «жидкость — пар» в однокомпонентных системах представляет интерес для многих отраслей химической технологии. Диаграмма фазовых равновесий позволяет получить сведения о поведении чистых компонентов при различных температурах и давлениях. Например, инженер-технолог с помощью диаграмм состояния может получить практически полную информацию об исследуемом объекте и провести технологический процесс в нужном направлении [2, 3].
Полученные результаты исследований могут быть использованы при изучении соответствующих учебных тем на факультативах и кружках в школе при подготовке к олимпиадам по химии [9, с. 100].
Литература:
- Физическая химия. В 2 кн. Кн. 1. Строение вещества. Термодинамика: учеб. для вузов / К. С. Краснов, Н. К. Воробьев, И. Н. Годнев и др.: под ред. К. С. Краснова. — 3-е изд., испр. — М.: Высш. шк., 2001. — 512 с.
- Есина, З. Н., Мурашкин, В. В., Корчуганова, М. Р. Фазовые диаграммы однокомпонентных систем // Вестник СГТУ. — 2012. — № 1 (64). — Выпуск 2. С. 50–53.
- Корчуганова, М. Р., Есина, З. Н. Прогнозирование фазового равновесия в однокомпонентных системах // Журнал физической химии. — 2015. — Том 89. — № 7. — С. 1062–1067.
- Петрухин, Н. В. Физическая химия: учеб. пособ. — М.: МО РФ, 2004. — 239 с.
- Физическая химия. Теоретическое и практическое руководство: учеб. пособие для вузов / Под ред. акад. Б. П. Никольского. — 2-е изд., перераб. и доп. — Л.: Химия, 1987. 880 с.
- Равновесие фаз [Электронный ресурс] Режим доступа: https://ru.wikipedia.org/wiki/Равновесие_фаз (дата обращения 25.03.2023).
- Клындюк, А. И., Петров, Г. С. Физическая химия: учеб. пособие для студентов. — Минск: БГТУ, 2010. — 273 с.
- Микрюков, В. Е. Курс термодинамики. — 3-е изд. — М: Учпедгиз, 1960. — 234 с.
- Богомолов, Д. А. Получение хромата аммония и изучение его химических свойств / Д. А. Богомолов, Ю. В. Соколова / Юный ученый. — 2022. — № 4 (56). — С. 98–100.

