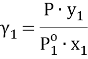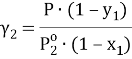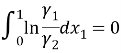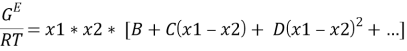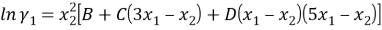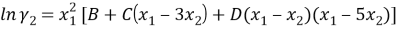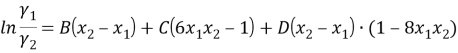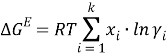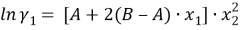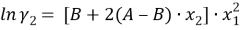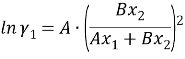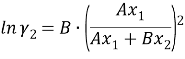В данной работе описываются способы определения коэффициентов активности изотермической системы пентан-ацетон с помощью эмпирических и полуэмпирических методов расчёта.
Ключевые слова: коэффициент активности, эмпирическая, полуэмпирическая модель, бинарная система.
Ацетон — органическое соединение, относящееся к классу кетонов. Бесцветная летучая жидкость, часто применяется в качестве растворителя.
Пентан — углеводород, относится к классу алканов. Бесцветная легколетучая жидкость, является сырьем для получения бензиновой фракции, изопрена.
Экспериментальные данные о составах равновесных фаз и общем давлении для системы пентан (1) — ацетон (2) при температуре 25°С представлены в таблице 1.
Таблица 1
Составы равновесных фаз для системы пентан (1) — ацетон (2) при общем давлении P и температуре 25°С
|
x 1, % мол. |
y1, %мол. |
Р, мм рт ст |
|
0,00 |
0,00 |
226,3 |
|
0,94 |
10,55 |
255,6 |
|
5,40 |
36,33 |
343,6 |
|
8,87 |
45,92 |
396,4 |
|
16,00 |
56,48 |
468,4 |
|
37,41 |
66,54 |
549,8 |
|
38,80 |
66,58 |
547,9 |
|
47,21 |
68,65 |
567,1 |
|
56,89 |
70,74 |
575,0 |
|
65,48 |
72,74 |
582,3 |
|
71,92 |
74,42 |
582,6 |
|
77,87 |
76,23 |
583,7 |
|
92,23 |
84,86 |
564,7 |
|
100,00 |
100,00 |
502,4 |
Коэффициенты активности по экспериментальным данным
Поскольку при заданной температуре в паровой фазе общее давление является довольно низким, а сильная ассоциация компонентов в этой фазе отсутствует, то паровую фазу можно считать идеальной, подчиняющейся закону Дальтона. Таким образом, расчет коэффициентов активности производится по формуле:
|
|
(1) | |
|
|
(2) |
где х 1 , у 1 — мольные доли пентана в жидкой и паровой фазе.
При x 1 = 0 общее давление соответствует давлению насыщенного пара второго компонента, а при x 1 = 100 % мол. — давлению насыщенного пара первого компонента. Таким образом, при 25°С Р° 1 = 502,4 мм рт. ст., а Р° 2 = 226,3 мм рт. ст.
Результаты расчетов значений γ i и связанных с ними величин, которые необходимы для проверки термодинамической согласованности равновесных данных методом Редлиха-Кистера, приведены в таблице 2.
Таблица 2
Коэффициенты активности компонентов, рассчитанные по экспериментальным данным
|
x1, мол.д. |
γ1 |
γ2 |
ln(γ1) |
ln(γ2) |
ln(γ1/γ2) |
|
0,0094 |
5,710 |
1,020 |
1,742 |
0,020 |
1,723 |
|
0,054 |
4,601 |
1,022 |
1,526 |
0,022 |
1,505 |
|
0,0887 |
4,085 |
1,039 |
1,407 |
0,039 |
1,369 |
|
0,16 |
3,291 |
1,072 |
1,191 |
0,070 |
1,121 |
|
0,3741 |
1,946 |
1,299 |
0,666 |
0,261 |
0,405 |
|
0,388 |
1,871 |
1,322 |
0,627 |
0,279 |
0,347 |
|
0,4721 |
1,641 |
1,488 |
0,496 |
0,398 |
0,098 |
|
0,5689 |
1,423 |
1,725 |
0,353 |
0,545 |
-0,192 |
|
0,6548 |
1,288 |
2,032 |
0,253 |
0,709 |
-0,456 |
|
0,7192 |
1,200 |
2,345 |
0,182 |
0,852 |
-0,670 |
|
0,7787 |
1,137 |
2,770 |
0,129 |
1,019 |
-0,890 |
|
0,9223 |
1,034 |
4,862 |
0,034 |
1,582 |
-1,548 |
Таблица 3
Коэффициенты активности компонентов, рассчитанные по экспериментальным данным для составления зависимости коэффициентов активности компонентов системы пентан (1)-ацетон (2) от состава
|
x1, мол.д. |
ln(γ1) |
ln(γ2) |
ln(γ1/γ2) |
|
0 |
1,757 |
-0,007 |
1,764 |
|
0,0094 |
1,742 |
0,020 |
1,723 |
|
0,054 |
1,526 |
0,022 |
1,505 |
|
0,0887 |
1,407 |
0,039 |
1,369 |
|
0,16 |
1,191 |
0,070 |
1,121 |
|
0,3741 |
0,666 |
0,261 |
0,405 |
|
0,388 |
0,627 |
0,279 |
0,347 |
|
0,4721 |
0,496 |
0,398 |
0,098 |
|
0,5689 |
0,353 |
0,545 |
-0,192 |
|
0,6548 |
0,253 |
0,709 |
-0,456 |
|
0,7192 |
0,182 |
0,852 |
-0,670 |
|
0,7787 |
0,129 |
1,019 |
-0,890 |
|
0,9223 |
0,034 |
1,582 |
-1,548 |
|
1 |
-0,029 |
1,926 |
-1,955 |
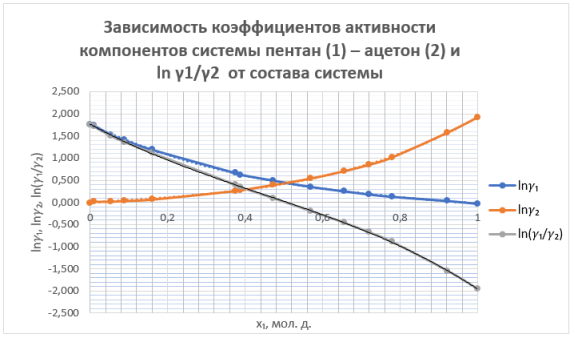
Рис. 1 Зависимость коэф. активности компонентов системы пентан (1)-ацетон (2) и ln(γ1/γ2) от состава системы
В соответствии с методом Редлиха-Кистера условие термодинамической согласованности равновесных данных выражается уравнением:
|
|
(3) |
Площадь под интегральной кривой в положительной области S 1 =0,4097, а в отрицательной области S 2 = 0,4217.
Площади S 1 и S 2 различаются на 0.012 (<0,02), что свидетельствует о корректности полученных экспериментальных данных о равновесии жидкость — пар.
Эмпирические модели Редлиха-Кистера
Эмпирические модели служат для математического описания массива экспериментальных данных о коэффициентах активности компонентов, они непригодны для корреляции и предсказания данных.
Одна из наиболее широко применяемых эмпирических моделей была предложена Редлихом и Кистером в 1948 г. В ней используется следующее разложение в ряд:
|
|
(4) |
где x 1 , x 2 — мольные доли компонентов в растворе.
Из него получаются следующие трехпараметрические уравнения для коэффициентов активности компонентов бинарной системы:
|
|
(5) | |
|
|
(6) |
Вычитая из уравнения (5) уравнение (6) и учитывая, что для бинарной системы x1 + x2 = 1, получаем:
|
|
(7) |
С использованием массива экспериментальных данных γ i (x i ) и уравнения (7), находят параметры B, C и D. Так, при x 1 = x 2 = 0.5 первое и третье слагаемое в правой части уравнения (7) обращается в 0 и рассчитывается значение C.
Интерполяцией вычисляем значение ln(γ1/γ2) = 0,0144, тогда константа С рассчитывается:
0,0144 = С • (6 • 0,5 • 0,5–1); C= 0,0287
При х 1 =0,1464 третье слагаемое в правой части уравнения (7) обращается в 0; ln(γ1/γ2) = 1,169, тогда константа В рассчитывается:
1,169 =В • ((1–0,1464) — 0,1464) — 0,0287 • (6 • 0,1464 • (1–0,1464) — 1); В = 1,669
При х 1 = 0,2113 ln(γ1/γ2) = 0,95 и из уравнения (7) рассчитывается константа D:
0,95 = 1, 669 • (0,7887–0,2113) + D • (0,7887–0,2113) • (1–8 • 0,2113 • 0,7887); D=0,0739
С использованием найденных констант В, С, D по уравнениям (5) и (6) рассчитывают значения lnγ 1 и lnγ 2 (табл. 4)
Таблица 4
Значения lnγ i , рассчитанные по эмпирическому уравнению Редлиха-Кистера
|
x 1 , мол. д. |
lnγ 1 |
lnγ 2 |
|
0,0094 |
1,678 |
0,0002 |
|
0,054 |
1,514 |
0,006 |
|
0,0887 |
1,394 |
0,015 |
|
0,16 |
1,172 |
0,046 |
|
0,3741 |
0,650 |
0,235 |
|
0,388 |
0,623 |
0,252 |
|
0,4721 |
0,470 |
0,367 |
|
0,5689 |
0,322 |
0,528 |
|
0,6548 |
0,212 |
0,701 |
|
0,7192 |
0,144 |
0,850 |
|
0,7787 |
0,092 |
1,006 |
|
0,9223 |
0,012 |
1,465 |
Маргулес
Для расчета констант уравнения Маргулеса с использованием линейного уравнения G E / ( RT • x 1 • x 2 ) = B + ( A — B ) • х 1 находят значения избыточной энергии Гиббса по уравнению:
|
|
(8) |
Таблица 5
Значения избыточной энергии Гиббса и функции G E /( RT * x 1 * x 2 )
|
x 1 , мол. д. |
G E , Дж/моль |
G E /(RT∙x 1 ∙x 2 ) |
|
0,0094 |
88,942 |
3,855 |
|
0,054 |
255,007 |
2,015 |
|
0,0887 |
396,734 |
1,981 |
|
0,16 |
617,628 |
1,855 |
|
0,3741 |
1022,748 |
1,763 |
|
0,388 |
1025,851 |
1,744 |
|
0,4721 |
1099,637 |
1,781 |
|
0,5689 |
1079,461 |
1,776 |
|
0,6548 |
1016,422 |
1,815 |
|
0,7192 |
917,821 |
1,834 |
|
0,7787 |
807,039 |
1,890 |
|
0,9223 |
381,273 |
2,147 |
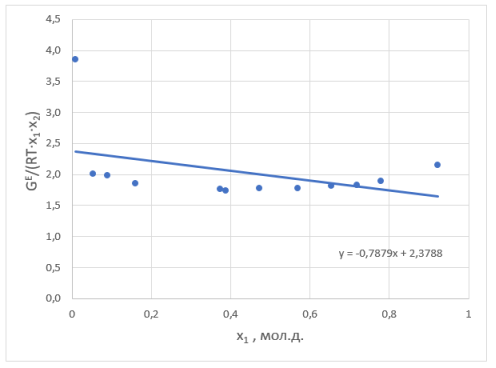
Рис. 2. Линейная зависимость G E / (RT • x 1 • x 2 ) = B + (A — B) • х 1 для расчета констант уравнения Маргулеса
По отрезку, отсекаемому прямой на оси ординат, находят параметр A (т. к. зависимость от x 1 ), а по значению тангенса угла наклона прямой рассчитывают второй параметр (параметр B) в уравнениях Маргулеса.
Судя по графику на рисунке 2, некоторые точки из таблицы 5 отклоняются от прямой. С учетом остальных точек строится прямая, отсекающая на оси ординат в соответствии с уравнением G E /(RT•x 1 •x 2 ) = B+(A-B)•х 1 отрезок, соответствующий константе A = 2,3788.
Тангенс угла наклона прямой tgα= -0,7879; tgα = A — B, следовательно, B = 3,1667. Далее с использованием уравнений Маргулеса:
|
|
(9) | |
|
|
(10) |
рассчитывают значения lnγ1 и lnγ2.
Таблица6
Значения lnγ i , рассчитанные по эмпирическому уравнению Маргулеса
|
x 1 , мол. д. |
lnγ 1 |
lnγ 2 |
|
0,0094 |
2,349 |
0,0001 |
|
0,054 |
2,205 |
0,005 |
|
0,0887 |
2,092 |
0,014 |
|
0,16 |
1,856 |
0,047 |
|
0,3741 |
1,163 |
0,305 |
|
0,388 |
1,120 |
0,332 |
|
0,4721 |
0,870 |
0,520 |
|
0,5689 |
0,609 |
0,805 |
|
0,6548 |
0,406 |
1,125 |
|
0,7192 |
0,277 |
1,409 |
|
0,7787 |
0,177 |
1,709 |
|
0,9223 |
0,023 |
2,590 |
Ван Лаар
Для определения констант уравнения Ван Лаара рассчитывают значения√(ln(γ1)) и √(ln(γ2)).
Таблица 7
Значения
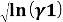
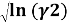
|
x 1 , мол. д. |
√ lnγ 1 |
√ lnγ 2 |
|
0,0094 |
1,320 |
0,140 |
|
0,054 |
1,235 |
0,147 |
|
0,0887 |
1,186 |
0,197 |
|
0,16 |
1,091 |
0,264 |
|
0,3741 |
0,816 |
0,511 |
|
0,388 |
0,792 |
0,528 |
|
0,4721 |
0,704 |
0,631 |
|
0,5689 |
0,594 |
0,738 |
|
0,6548 |
0,503 |
0,842 |
|
0,7192 |
0,427 |
0,923 |
|
0,7787 |
0,359 |
1,009 |
|
0,9223 |
0,183 |
1,258 |
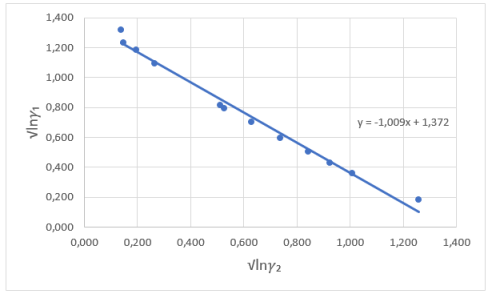
Рис. 3. Линейная зависимость для определения констант уравнения Ван Лаара
Отрезок, отсекаемый прямой на оси ординат, соответствует
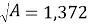
Тангенс угла наклона прямой tgα = -1,009;
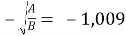
С помощью уравнения Ван Лаара рассчитывают значения ln(γ1) и ln(γ2). Уравнения Ван Лаара:
|
|
(11) | |
|
|
(12) |
Таблица 8
Значения lnγ i , рассчитанные по эмпирическому уравнению Ван Лаара
|
x 1 , мол. д. |
lnγ 1 |
lnγ 2 |
|
0,0094 |
1,847 |
0,0002 |
|
0,054 |
1,681 |
0,006 |
|
0,0887 |
1,558 |
0,015 |
|
0,16 |
1,321 |
0,049 |
|
0,3741 |
0,728 |
0,265 |
|
0,388 |
0,695 |
0,284 |
|
0,4721 |
0,516 |
0,420 |
|
0,5689 |
0,343 |
0,608 |
|
0,6548 |
0,219 |
0,803 |
|
0,7192 |
0,145 |
0,966 |
|
0,7787 |
0,090 |
1,130 |
|
0,9223 |
0,011 |
1,577 |
Литература:
- Гайле, А. А. Процессы разделения и очистки продуктов переработки нефти и газа / А. А. Гайле, В. Е. Сомов, А. В. Камешков. — 2. — 2018: Химиздат, 2018. — 432 с.