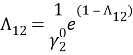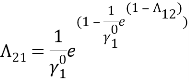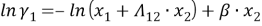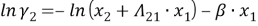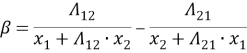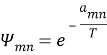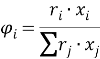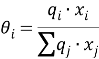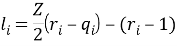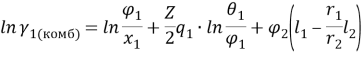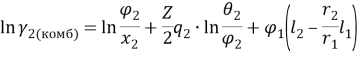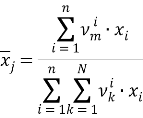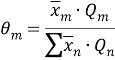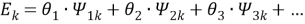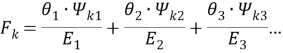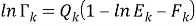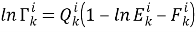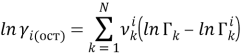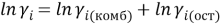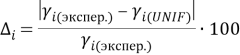Сравнение эмпирических, полуэмпирических и теоретической моделей активности равновесия «жидкость — пар» на примере бинарной системы «пентан — ацетон»



В данной работе описываются способы определения коэффициентов активности изотермической системы пентан — ацетон с помощью полуэмпирического метода расчёта и теоретической модели UNIFAC, а также их сравнение с эмпирическими моделями.

Ключевые слова: коэффициент активности, UNIFAC, полуэмпирическая модель, бинарная система.

Полуэмпирическая модель Вильсона

Наибольшее распространение получила модель «локальных составов» (или «локальных концентраций»). Первое уравнение, основанное на этой модели, было выведено в 1964 г. Вильсоном. Модель «локальных составов» основана на том, что в результате межмолекулярных взаимодействий в смеси возникают локальные микросоставы, неэквивалентные макросоставу раствора по приготовлению. Различие локальных и средних концентраций компонентов связано с разностью энергий взаимодействия одноименных и разноименных пар молекул.

По данным статьи [1, с. 3] из графика зависимости коэффициентов активности компонентов системы пентан (1) — ацетон (2) и ln γ1/γ2 от состава системы экстраполяцией кривой lnγ ₁ =f(x ₁ ) находят при х ₁ =0 lnγ ⁰ ₁ = 1,7572 и γ ⁰ ₁ = 5,796, а экстраполяцией зависимости lnγ ₂ =f(x ₂ ) при х ₁ =1 определяют lnγ ⁰ ₂ = 1,9257 и γ ⁰ ₂ = 6,86.

Т. к. система с положительным отклонением от закона Рауля, то по номограмме (рисунок 1) ориентировочные значения приведенных параметров уравнения Вильсона: Λ ₁₂ = 0,38 и Λ ₂₁ = 0,3.

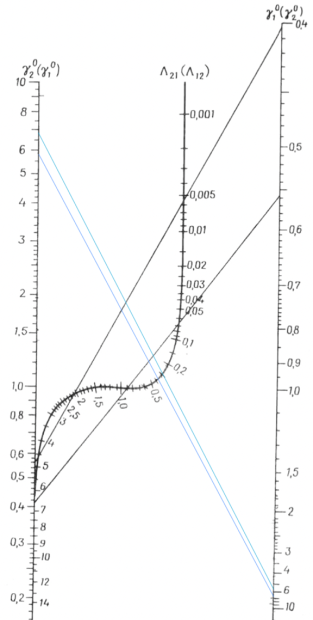
Рис. 1. Номограмма для определения приведенных параметров уравнения Вильсона

Далее рассчитывают уточненные значения приведенных параметров по уравнениям:

		(1)
		(2)

Отсюда получим, что Λ ₁₂ = 0,379 и Λ ₂₁ = 0,314

		(3)
		(4)
		(5)

Далее находят значения β и lnγi по уравнениям:

Таблица 1

Коэффициенты активности компонентов, рассчитанные по методу Вильсона

x1, мол. д.	β	lnγ1	lnγ2
0,0094	0,669	1,618	0,0002
0,054	0,593	1,446	0,006
0,0887	0,539	1,326	0,015
0,16	0,440	1,107	0,046
0,3741	0,198	0,616	0,223
0,388	0,183	0,590	0,238
0,4721	0,099	0,450	0,344
0,5689	0,003	0,313	0,493
0,6548	-0,088	0,211	0,654
0,7192	-0,161	0,147	0,796
0,7787	-0,235	0,096	0,947
0,9223	-0,457	0,014	1,423

Сравнение эмпирических и полуэмпирических методов

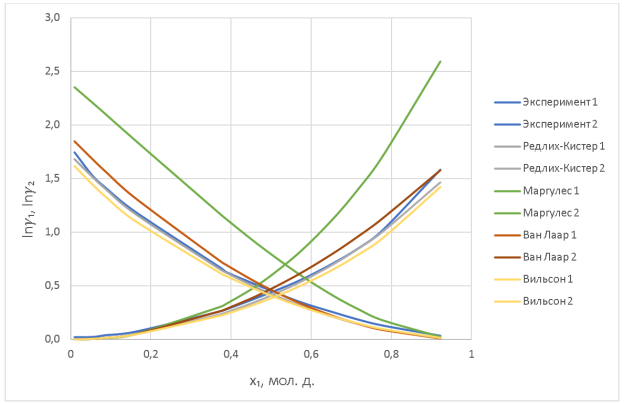
Рис. 2. Зависимость 𝛄 _i компонента системы пентан — ацетон от состава при 25 ^о С

Было произведено сравнение эмпирических методов, описанных в статье [1] и полуэмпирического метода. Для математического описания зависимости коэффициентов активности компонентов системы пентан — ацетон лучше всего использовать уравнение Редлиха-Кистера.

Теоретические модель. Метод UNIFAC ( UNIquac Functional — group Activity Coefficients )

Расчет коэффициентов активности компонентов системы пентан (1) — ацетон (2) при х ₁ = 0.16 и температуре 25°С (298.15 К) методом UNIFAC.

Молекула пентана представляется в виде 3 групп СН ₂ и 2 групп СН ₃ , а молекула ацетона — как 1 группа CH ₃ CO и 1 группа СН ₃ . Параметры объема R _k и поверхности групп Q _k приведены в таблице 2.

Параметры взаимодействия групп: а ₁₂ = 0, а ₁₃ = 476,4, а ₂₁ = 0, а ₂₃ = 476,4, а ₃₁ = 26,76; а ₃₂ = 26,76. Приведенные параметры группового взаимодействия, рассчитанные по уравнению:

(6)

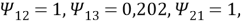
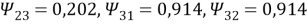
Таблица 2

Параметры объема и поверхности групп СН ₂ , CH ₃ и CH ₃ CO

N группы	Группа	R k	Q k	Количество групп в молекуле
				Пентан	Ацетон
1	СН 2	0,6744	0,540	3	0
2	СН 3	0,9011	0,848	2	1
3	CH 3 CO	1,6724	1,488	0	1

Ван-дер-ваальсовы радиусы молекул компонентов:

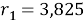
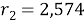
Ван-дер-ваальсовы поверхности молекул компонентов:

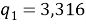
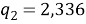
Объемная доля компонентов в растворе, рассчитанная по уравнению:

(7)

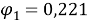
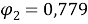
Доля площади поверхности молекул компонентов в растворе, рассчитанная по уравнению:

(8)

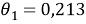
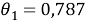
Факторы объемности молекул компонентов, рассчитанные по уравнению:

(9)

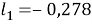
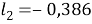
Далее используют уравнения:

		(10)
		(11)

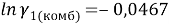
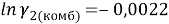
Групповые доли групп в растворе при х ₁ =0,16, рассчитанные по уравнению:

(12)

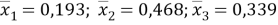
Доля площади поверхности групп в растворе рассчитывается по уравнению:

(13)

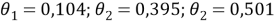
Молекула пентана на 0,6 состоит из группы СН ₂ и на 0,4 из группы СН ₃ , а молекула ацетона на 0,5 состоит из группы СН ₃ и на 0,5 из группы СН ₃ CO, поэтому расчет был произведен и для раствора, и для чистых компонентов, результаты представлены в таблице 3.

Таблица 3

Доля площади поверхности групп в растворе и в чистых компонентах

Параметр	Раствор	Пентан	Ацетон
θ 1	0,104	0,489	-
θ 2	0,395	0,511	0,363
θ 3	0,501	-	0,637

Средневзвешенные параметры взаимодействия групп рассчитывают по уравнению:

(14)

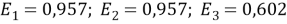
Таблица 4

Средневзвешенные параметры взаимодействия групп в растворе и для чистых компонентов

Параметр	Раствор	Пентан	Ацетон
E 1	0,957	1	-
E 2	0,957	1	0,945
E 3	0,602	-	0,710

Значения дополнительной функции F _i рассчитывают по уравнению (15) и приводят для раствора и чистых компонентов в табл. 5:

(15)

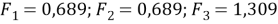
Таблица 5

Дополнительные функции групп в растворе и для чистых компонентов

Параметр	Раствор	Пентан	Ацетон
F 1	0,689	1	-
F 2	0,689	1	0,565
F 3	1,309	-	1,248

Коэффициенты активности групп в растворе рассчитываются по уравнению (16) и в чистых компонентах — по уравнению (17):

(16)

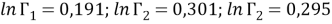
(17)

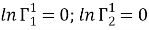
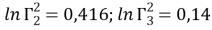
Далее рассчитывают коэффициенты активности компонентов с учетом остаточной и комбинаторной составляющих по уравнениям (18) и (19):

(18)

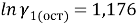
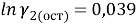
(19)

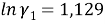
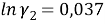
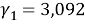
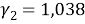
Погрешность расчета γ ₁ и γ ₂ методом UNIFAC составляет при х ₁ = 0,16:

(20)

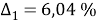
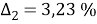
Литература:

1. Цымлякова, Ю. Д. Проверка адекватности эмпирических и полуэмпирических моделей при изучении фазового равновесия в бинорной системе «углеводород — апротонный растворитель» / Ю. Д. Цымлякова. — Текст: непосредственный // Молодой ученый. — 2022. — № 26 (421). — С. 1–7. — URL: https://moluch.ru/archive/421/93746/ (дата обращения: 08.07.2022).
2. Гайле, А. А. Процессы разделения и очистки продуктов переработки нефти и газа / А. А. Гайле, В. Е. Сомов, А. В. Камешков. — 2. — 2018: Химиздат, 2018. — 432 с.
3. Уэйлес, С. Фазовые равновесия в химической технологии. Ч. 1, 2. — М.: Мир, 1989. — 664 с.