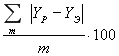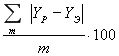В работе разрабатывается корреляционно-предсказывающая модель с использованием модифицированного уравнения Вильсона, позволяющая для заданных значений концентраций в жидкой фазе X с достаточной степенью точности получать расчетные значения концентраций в паровой фазе Y, температуры Т и давления Р. Показано, что модель UNIFAC на основе модифицированного уравнения Вильсона позволяет получать физико-химические показатели для тех бинарных смесей, по которым отсутствуют экспериментальные данные. Применение предложенного подхода позволяет достоверно описывать фазовое равновесие многокомпонентной смеси.
Ключевые слова: фазовое равновесие, локальные объемные доли, мольные доли, математическая модель, жидкая фаза, паровая фаза, корреляционно-предсказывающая модель,прогнозирование равновесных составов, многокомпонентная смесь, ректификация, разделение смесей, азеотропия.
В подавляющем большинстве случаев разделяемые методом ректификации смеси являются неидеальными, в результате чего в двухфазных смесях жидкость — пар возникают явления азеотропии, а также расслаивания жидкости. Появление гомогенных, либо гетерогенных азеотропов кардинально меняет характер ее разделения вплоть до невозможности выделения целевых продуктов. Таким образом, протекание процесса ректификации тесно связано с равновесными составами парожидкостной системы как предельно достижимыми на ступенях разделения. Поэтому при математическом моделировании прогнозирование равновесных составов в ходе ректификации смесей представляет собой важную задачу.
Прогнозирование равновесных составов фаз в бинарных и многокомпонентных реальных смесях основывается на учете их отклонения от идеального поведения с помощью коэффициентов активности 
компонентов в фазах. Это в особенности относится к азеотропным смесям, специфика поведения которых полностью отражается коэффициентами активности присутствующих компонентов.
Для описания зависимости коэффициентов активности компонентов от состава фазы предложен ряд полуэмпирических уравнений.
Большинство моделей растворов основывается на предположении об одинаковых или близких по размеру и форме молекул в растворе. Такое предположение позволяет значительно упростить расчет, однако приводит к заведомо неверным результатам, если молекулы реального раствора сильно различаются по размерам [1], как, например, молекулы в растворах полимеров. Таким образом, при микроскопическом рассмотрении жидкая смесь не является однородной, т. е. состав в одной точке смеси отличается от состава в другой. Хотя в инженерных приложениях используется только средняя концентрация компонентов в смесях, для построения адекватной модели жидкой смеси необходимо оперировать локальными составами.
Выражения, полученные Флори для термодинамических функций в растворах полимеров, были использованы Вильсоном [2] для обычных растворов, однако вместо средних объемных долей он ввел «локальные» объемные доли компонентов:
(1)
где 
- энергия смешения Гиббса;
Согласно концепции локальных составов, введенной Вильсоном, распределение молекул относительно центральной молекулы имеет вид
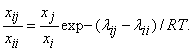(2)
где
— локальный состав, определенный как число молекул типа i-j в окрестности центральной молекулы, деленное на общее число молекул 
; 
- параметр, характеризующий энергию взаимодействия между парами i-i и i-j.
С учетом введенных локальных концентраций локальные объемные доли 
компонента i в уравнении могут быть определены как
(3)
где 
— мольные объемы чистых компонентов i и j.
Подстановка уравнения (3) в (1) дает зависимость избыточной энергии смешения Гиббса от состава и температуры смеси. Дифференцирование полученного выражения по составу смеси дает широко известное уравнение Вильсона, связывающее коэффициент активности компонента в смеси 
, с ее составом и температурой:
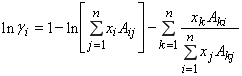, (4)
В уравнении (4) ее составляющие определяются по следующим соотношениям:
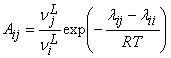, (5)
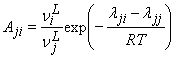, (6)
В модели Вильсона для описания многокомпонентных смесей (МКС) требуется только задать параметры
, определяемые по экспериментальным данным для бинарных смесей, входящих в данную МКС, и физико-химические свойства чистых компонентов.Для прогнозирования фазового равновесия наиболее приемлемой оказалась групповая модель раствора, позволяющая предсказывать равновесные соотношения в смесях гомологического ряда на основе экспериментальных данных одной смеси того же ряда.
В соответствии с групповой моделью раствора коэффициент активности представляется в виде:
(7)
где индекс i соответствует типу молекулы;
— составляющая, связанная с взаимодействием групп (учитывает энергию взаимодействия групп);
— составляющая, связанная с размером молекулы.
Однако это уравнение не учитывает форму молекулы и поэтому может дать неверные результаты для изомерных молекул. Групповой вклад 
в логарифм коэффициента активности полагают равным сумме индивидуальных вкладов каждой группы, т. е. допускается, что все группы действуют независимо. Отсюда групповой коэффициент определяется так же, как и молекулярный.
(8)
где 
- число групп типа k в молекуле i;
— коэффициент активности группы в стандартном состоянии.
В общем виде групповой коэффициент активности является функцией только группового состава, температуры и давления.
(9)
Это уравнение позволяет распространять термодинамические свойства одной системы на другие, имеющие тот же групповой состав.
Групповая доля “x” рассчитывается по компонентному составу смеси с учетом числа и типа групп.
(10)
Различными авторами было предложено несколько аналитических зависимостей для 
[3,4,5]. Для функции 
предлагались уравнения: Вильсона, NRTL, UNIQUAC.
Наиболее полный набор параметров группового взаимодействия представлен в работах [6] для модели UNIFAC. В этом методе значение 
, подставляемое в выражение (8) имеет вид:
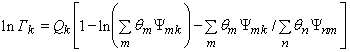(11)
где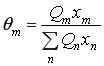 
(12)
(13)
(14)
- поверхностная доля структуры группы т;
- мольная доля структурной группы т;
и 
параметры структурных групп m и п, учитывающие силы взаимодействия между структурными группами и определяемые параметрами взаимодействия групп 
и, которые в первом приближении не зависят от температуры.
Хотя корректность метода UNIFAC проверена на примере бинарных систем «жидкость-пар», ценность его заключается в возможности применения его для многокомпонентных смесей. Особенно это важно для систем, в которых проведение экспериментальных исследований не представляется возможным.
Для восполнения информации о фазовом равновесии в бинарных системах, где отсутствуют экспериментально определенные данные, в работе использована корреляционно-предсказывающая модель UNIFAC. Наиболее полный набор параметров группового взаимодействия для этой модели представлен в [7].
В этой модели значение Гk имеет вид:
,
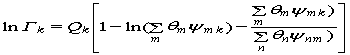где: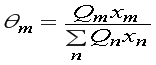 
,
,
,
где — θm — поверхностная доля структуры группы m; Хm — мольная доля структурной группы m; Ψmn и Ψnm — параметры структурных групп m и n, учитывающие силы взаимодействия между структурными группами и определяемые параметрами взаимодействия групп аmn и аnm, которые в первом приближении не зависят от температуры.
Однако, в связи с возможностью довольно больших погрешностей предсказания в отдельных случаях (что отмечается самими авторами) представлялось целесообразным провести проверку качества предсказания в тех гомологических рядах, в которые входят недостающие системы, по двум моделям: модифицированная модель Вильсона и модель UNIQUAC. Результаты сравнения предсказанных по групповой модели и экспериментальных данных по фазовому равновесию жидкость-пар представлены в табл. 1.
Таблица 1
Отклонения предсказанных данных по фазовому равновесию жидкость-пар от экспериментальных
|
Предсказанные системы |
Модель Вильсона |
Модель UNIQUAC |
|
Метилэтилкетон-уксусная кислота |
1.48 |
3.3 |
|
Ацетальдегид-винилацетат |
4.0 |
7.15 |
|
Метилэтилкетон-изопропанол |
1.1 |
3.2 |
|
Метанол-бутанол |
1.4 |
1.4 |
|
Пропанол-этанол |
0.8 |
1.1 |
|
Метанол-вода |
2.3 |
3.1 |
|
Изопропанол-вода |
1.05 |
2.7 |
|
Метанол- метилэтилкетон |
1.7 |
2.6 |
|
Метилэтилкетон-бутанол |
4.0 |
5.3 |
|
Пропанол-пропилацетат |
0.91 |
1.3 |
|
Метанол-этилацетат |
1.8 |
2.1 |
|
Метанол-пропилацетат |
2,3 |
2,9 |
|
Этилацетат- метилэтилкетон |
2.4 |
2.9 |
|
Ацетон-винилацетат |
1.1 |
2.3 |
|
Ацетон-этилацетат |
1.4 |
2.1 |
Результаты показали, что средняя абсолютная погрешность при использовании модели UNIQUAC в ряде случаев составляет более 7 %. Такое качество предсказания нельзя считать удовлетворительным. Поэтому была проведена модификация групповой модели, основанная на модифицированном уравнении Вильсона:
,
где 
,
,
.
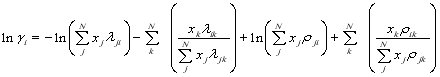Для выявления моделирующих возможностей нового уравнения локальных составов, а также для получения модели полного фазового равновесия были определены молекулярные параметры этого уравнения.
Сопоставление результатов расчета по двум методикам (табл.1) показало, что данные, полученные по методике UNIFAС уступают по качеству предсказания. Вероятными причинами низкого качества предсказания по методике UNIFАC могут быть:
– недостаточно корректные данные базовой смеси, по которой определялись значения групповых параметров;
– погрешность, допущенная при оценке параметров;
– закрепление групповых параметров, определенных по экспериментальным данным других гомологических рядов.
На основании использования разработанных пакетов прикладных программ решена проблема прогнозирования равновесных соотношений в многокомпонентных смесях. Показано, что модель UNIFAC на основе модифицированного уравнения Вильсона позволяет получать физико-химические показатели для тех бинарных смесей, по которым отсутствовали экспериментальные данные. Применение предложенного подхода позволило полно и достоверно описать фазовое равновесие многокомпонентной смеси в производстве этилового спирта и успешно решить одну из основных проблем описания и прогнозирования сложных равновесных соотношений в виде системы нелинейных алгебраических уравнений, описывающих многокомпонентную ректификацию.
Литература:
- Fredenslund A., Jones R. L., Prausnits J. M. Groupcontribution estimation of activity coefficients in nonideal liquid mixtures // AIChE Journal. — Houston, 1995. –№ 21. –РР. 1086–1098.
- Кафаров В. В., Ветохин В. Н. Основы построения операционных систем в химической технологии. — М.: Наука, 1990. — 452 с.
- Eckert C. A., Thomas E. R., Newman B. A., Nicolaides G. L. Limiting activity coefficients from differential ebulliometry // Journal Chem. Eng. Data. — Pittsburgh, 1992. –№ 27. –РР. 233–240.
- Мозжухин А. С., Митропольская В. А., Рябин А. И. Компьютерная система автоматизированного экспериментального исследования парожидкостного равновесия // ХIV Межд. конф. по химической термодинамике: Тез. докл. –C.-П.Б., 2002. — С. 465–469.
- Abbott M. M., Van Ness H. C. Vapor-liquid equilibrium. Part 3: Data reduction with precise expressions for GE // AIChE Journal. — Houston, 1995. –№ 21. –РР. 62–71.
- Сорокин В. С. Макроскопическая необратимость и энтропия. Введение в термодинамику. –М.: ФИЗМАТЛИТ, 2004. -176 с.
- Konstantinov Eu.N. Effect of muiticomponent mass-transfer on therectificationcalculation with allowance to heat balance / Eu.N. Konstantinov, T. G. Korolkova, B. M. Achmiz II The First European Congress Chemical Engineering Florence (Italy), May 4–7, 1997. Event 601 offiFCE.
