В данной статье рассмотрены основные и дополнительные теоремы об индексе оператора и дефектных числах, которые имеют большое теоретическое значение в изучении дифференциальных и операторных уравнений.
Ключевые слова: оператор, индекс.
Обозначения и основные теоремы
Пусть имеем банаховы пространства
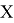
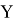

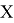
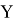
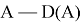
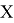
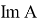
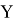
Оператор

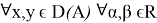
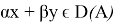
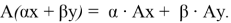
Оператор

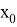
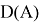
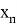
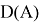
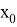
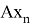
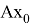
Оператор

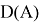
Оператор

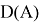
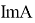
Теорема 1.
Оператор

Теорема 2.
Оператор


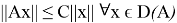
Нормой ограниченного օператора

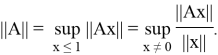
Под суммой двух операторов
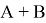
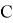
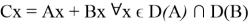
Теорема 3.

Пусть оператор

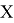
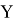
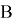
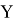
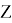

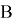
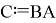
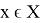
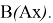
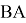
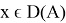
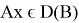
Теорема 4.
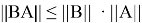
Оператор

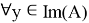
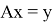
имеет единственное решение, а оператор
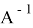
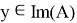
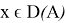

Теорема 5.
Если линейный оператор

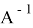
Теорема 6 (Теорема Банаха об обратном).
Если оператор

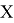
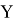

Линейным функционалом над линейным пространством
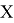
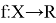
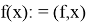
Сопряженным пространством линейного пространства
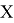
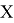
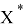
Сопряженным оператором линейного оператора
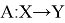
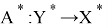
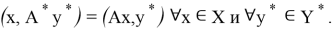
Легко заметить, что сопряженный оператор также линеен.
Теорема 7.
Если

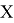
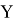
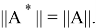
Ядром оператора

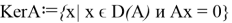
Легко заметить, что ядро линейного оператора является линейным подпространством линейного пространства
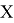
Ядро сопряженного оператора
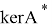
Если размерность ядра и коядра оператора

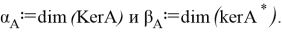
А пара
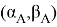

Если оба из этих чисел конечны, то говорят, что оператор обладает конечной d-характеристикой.
Теорема 8.
Коядро конечномерно тогда и только тогда, когда конечномерно фактор пространство
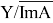
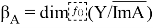
Линейным аннигилятором подпространства
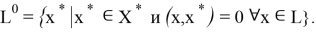
Заметим, что если
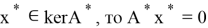
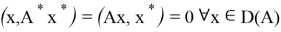
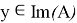
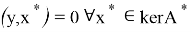
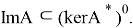
Оператор

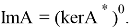
Теорема 9.
Оператор

Доказательство:
Пусть оператор

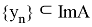

Докажем, что
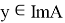
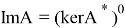
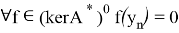
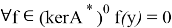

Пусть теперь образ оператора

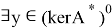
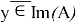
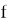
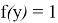
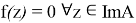
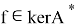
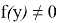
Таким образом теорема доказана!
Оператор

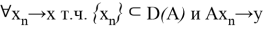
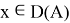
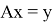
Оператор

-
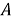
-
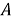
-
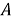
Индексом оператора

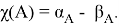
Заметим также, что оператор

Оператор

Теоремы о дефектных числах и индекса оператора
Теорема 1.
Пусть
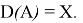

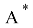
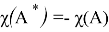
Доказательство:
Пусть

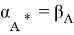
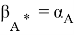
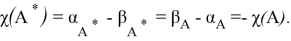
Теорема доказана!
Теорема 2.
Пусть

1. Если
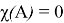

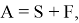
где
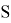
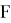
2. Если
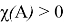

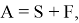
где
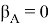
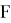
3. Если
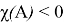

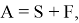
где
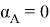
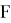
Доказательство:
Пусть
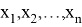
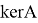
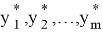
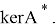
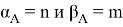
Согласно теореме Хана-Банаха, существуют такие непрерывные линейные функционалы
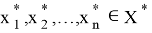
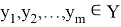
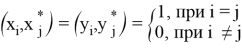
Обозначим
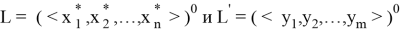
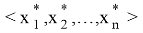
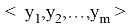
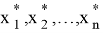
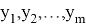
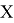
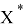
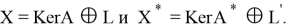
Рассмотрим теперь указанные 3 случая.
1. Если
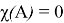
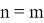
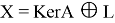
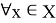
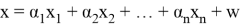
однозначным образом, где
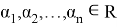
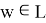
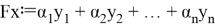
и рассмотрим оператор
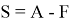
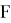
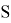
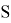
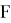
2. Если
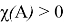
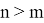
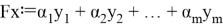
Аналогично предыдущему случаю, оператор
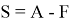
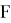
3. Если
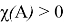
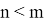
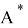
Таким образом, теорема доказана!
Заметим также, что во всех трех случаях оператор
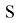
Для следующей теоремы нам понадобится лемма.
Лемма
. Псуть
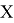
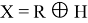
Где
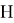
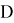
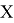
1.
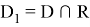
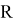
2. Пространство
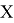
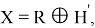
Где
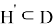
Доказательство:
Пусть
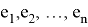
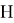
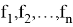
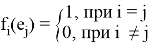
и
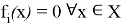
Пусть
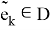
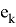
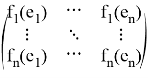
отличен от нуля.
Возьмем
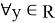
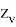
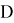
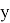
Обозначим
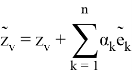
Так как определитель вышеуказанной матрицы отличен от нуля, то можем подобрать
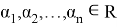
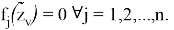
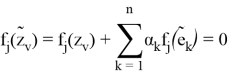
Так как
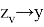
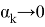
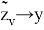
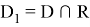
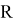
Обозначим
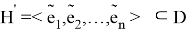
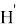
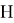
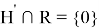
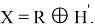
Лемма доказана!
Теорема 3.
Если

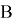
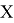
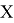
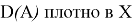
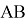
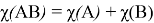
Доказательство:
Обозначим
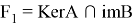
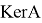
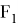
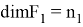
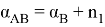
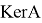
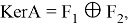
Где
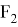
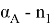
В силу доказанной леммы
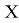
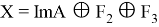
Где

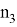
Таким образом
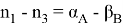
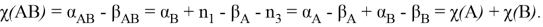
Литература:
- The Index of Elliptic Systems of Singular Integral Operators* R. T. SEELEY JOURNAL OF MATHEMATICAL ANALYSIS AND APPLICATIONS 7, 289–309 (1963)
- И. Ц. Гохберг, М. Г. Крейн, Основные положения о дефектных числах, корневых числах и индексах линейных операторов, УМН, 1957, том 12, выпуск 2(74), 43–118
- А. И. Вольперт, Об индексе и нормальной разрешимости граничных задач для эллиптических систем дифференциальных уравнений на плоскости, Тр. ММО, 1961, том 10, 41–87
- А. Н. Колмогоров, С. В. Фомин, Элементы теории функций и функционального анализа

