В статье проведено полное исследование условной устойчивости нулевого решения линейного разностного уравнения третьего порядка в критических случаях (когда значения коэффициентов уравнения находятся на границе области устойчивости). Дано полное описание всех подпространств начальных условий, относительно которых нулевое решение уравнения является условно устойчивым в критических случаях.
Ключевые слова: разностное уравнение третьего порядка, условная устойчивость, пространство начальных условий, область устойчивости
Введение ипостановка задачи
Исследование устойчивости решений дискретных систем (разностных уравнений) является одной из важнейших задач. Известно, что для линейных уравнений эта задача сводится к выяснению расположения относительно единичной окружности на комплексной плоскости корней характеристического полинома. Наиболее сложными для изучения являются так называемые критические случаи (называемые также граничной устойчивостью), когда некоторые корни характеристического полинома на комплексной плоскости попадают на единичную окружность. В теории устойчивости изучение критических случаев напрямую связано с исследованием границы области асимптотической устойчивости в пространстве параметров [1, 3].
В последнее время наряду с исследованием классической устойчивости (по Ляпунову) большое внимание уделяется условной устойчивости [1, 3]. В отличие от непрерывных систем [4], проблема условной устойчивости для дискретных систем изучена мало [1–3]. Цель нашей работы: провести полное исследование условной устойчивости нулевого решения линейного разностного уравнения третьего порядка
![]() ,(1)
,(1)
где ![]() в критических случаях, когда коэффициенты
в критических случаях, когда коэффициенты ![]() лежат на границе области асимптотической устойчивости.
лежат на границе области асимптотической устойчивости.
Область асимптотической устойчивости уравнения (1) в пространстве коэффициентов ![]() полностью исследована в [3] и изображена на рис. 1. Она представляет собой тело, ограниченное гиперболическим параболоидом
полностью исследована в [3] и изображена на рис. 1. Она представляет собой тело, ограниченное гиперболическим параболоидом ![]() и двумя плоскостями
и двумя плоскостями ![]() ,
, ![]() .
.
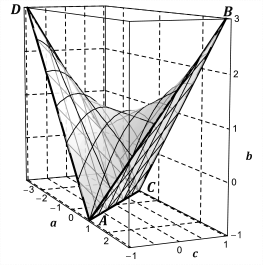
Рис. 1. Область асимптотической устойчивости уравнения (1)
Границу области асимптотической устойчивости уравнения (1) образуют четыре вершины: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , пять ребер: AC, AD и CD, AB и CB, две грани ACD и ABC и часть гиперболического параболоида.
, пять ребер: AC, AD и CD, AB и CB, две грани ACD и ABC и часть гиперболического параболоида.
Определение. Нулевое решение уравнения (1) называется условно устойчивым относительно подпространства W пространства начальных условий ![]() , если любое решение уравнения (1) с начальными условиями из подпространства W ограничено.
, если любое решение уравнения (1) с начальными условиями из подпространства W ограничено.
Будем говорить, что уравнение (1) условно устойчиво относительно подпространства W, если его нулевое решение условно устойчиво относительно подпространства W.
В данной статье мы полностью описываем все подпространства W начальных условий, относительно которых нулевое решение уравнения (1) является условно устойчивым в критических случаях.
Основные результаты
Как следует из результатов работы [3], на границе области асимптотической устойчивости потеря устойчивости может произойти только в вершинах ![]() ,
, ![]() ,
, ![]() ,
, ![]() и на ребрах AB:
и на ребрах AB: ![]() , CD:
, CD: ![]() (в остальных случаях решения уравнения (1) ограничены при любых начальных условиях). Рассмотрим все эти критические случаи.
(в остальных случаях решения уравнения (1) ограничены при любых начальных условиях). Рассмотрим все эти критические случаи.
Случай 1. Вершина![]() :
: ![]()
![]()
![]() .
.
Общее решение уравнения (1) имеет вид![]()
Зададим начальные условия![]() . Тогда, решая систему
. Тогда, решая систему
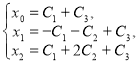
относительно ![]() , получаем
, получаем ![]() ,
, ![]() ,
, ![]() . Для ограниченности решений в этом случае необходимо и достаточно, чтобы
. Для ограниченности решений в этом случае необходимо и достаточно, чтобы ![]() . В пространстве начальных значений
. В пространстве начальных значений ![]() уравнение
уравнение ![]() задает плоскость
задает плоскость ![]() , проходящую через
, проходящую через ![]() . Получаем следующее
. Получаем следующее
Утверждение 1. Уравнение (1) условно устойчиво в критическом случае ![]()
![]()
![]() тогда и только тогда, когда начальные условия уравнения (1) принадлежат подпространству
тогда и только тогда, когда начальные условия уравнения (1) принадлежат подпространству ![]() .
.
В случае условной устойчивости каждое решение уравнения (1) имеет вид ![]() . Все решения являются периодическими с периодом 2 (см. пример на рис. 2).
. Все решения являются периодическими с периодом 2 (см. пример на рис. 2).
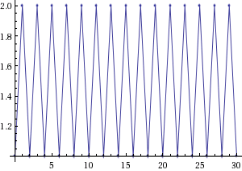
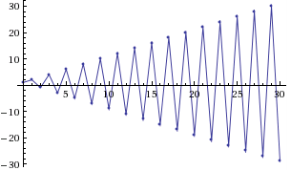
Рис. 2. Примеры решений с начальными условиями, удовлетворяющими (слева) и не удовлетворяющими (справа) уравнению плоскости![]()
На рисунке 2 слева показана условная устойчивость для начальных значений ![]()
![]() ,
, ![]() , удовлетворяющих уравнению плоскости
, удовлетворяющих уравнению плоскости ![]() (решение имеет вид
(решение имеет вид ![]() ). Справа показана неустойчивость для начальных значений
). Справа показана неустойчивость для начальных значений ![]() ,
, ![]() ,
, ![]() , не удовлетворяющих уравнению плоскости
, не удовлетворяющих уравнению плоскости ![]() (решение имеет вид
(решение имеет вид ![]() ).
).
Случай 2. Вершина ![]() :
: ![]()
![]()
![]() .
.
Общее решение уравнения (1) имеет вид ![]() .
.
Зададим начальные условия![]() . Тогда, решая систему
. Тогда, решая систему
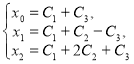
относительно ![]() , получаем
, получаем ![]() ,
, ![]() ,
, ![]() . Для ограниченности решений в этом случае необходимо и достаточно, чтобы
. Для ограниченности решений в этом случае необходимо и достаточно, чтобы ![]() . Получаем аналогичное случаю 1 следующее
. Получаем аналогичное случаю 1 следующее
Утверждение 2. Уравнение (1) условно устойчиво в критическом случае ![]()
![]()
![]() тогда и только тогда, когда начальные условия уравнения (1) принадлежат подпространству
тогда и только тогда, когда начальные условия уравнения (1) принадлежат подпространству ![]() .
.
В случае условной устойчивости каждое решение уравнения (1) имеет вид ![]() . Как и в случае 1, все решения являются периодическими с периодом 2.
. Как и в случае 1, все решения являются периодическими с периодом 2.
Случай 3. Вершина![]() :
: ![]()
![]()
![]() .
.
Общее решение уравнения (1) имеет вид ![]()
Зададим начальные условия ![]() . Тогда, решая систему
. Тогда, решая систему
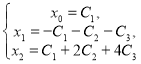
относительно ![]() , получаем
, получаем ![]() ,
, ![]() ,
, ![]() . Для ограниченности решений в этом случае необходимо и достаточно, чтобы
. Для ограниченности решений в этом случае необходимо и достаточно, чтобы ![]() и
и ![]() . В пространстве начальных значений
. В пространстве начальных значений ![]() эти уравнения задают прямую
эти уравнения задают прямую ![]() . Каноническое уравнение прямой имеет вид
. Каноническое уравнение прямой имеет вид ![]() .
.
Получаем следующее
Утверждение 3. Уравнение (1) условно устойчиво в критическом случае ![]()
![]()
![]() тогда и только тогда, когда начальные условия уравнения (1) принадлежат подпространству
тогда и только тогда, когда начальные условия уравнения (1) принадлежат подпространству ![]() .
.
В случае условной устойчивости каждое решение уравнения (1) имеет вид ![]() . Все решения являются периодическими с периодом 2 (см. пример на рис. 3).
. Все решения являются периодическими с периодом 2 (см. пример на рис. 3).
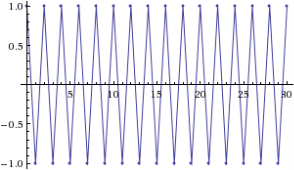
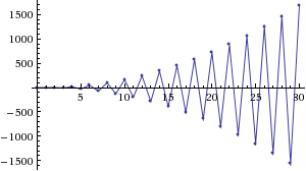
Рис. 3. Примеры решений с начальными условиями, удовлетворяющими (слева) и не удовлетворяющими (справа) уравнению прямой ![]()
На рисунке 3 слева показана условная устойчивость для начальных значений ![]()
![]() ,
, ![]() , удовлетворяющих уравнению прямой
, удовлетворяющих уравнению прямой ![]() (решение имеет вид
(решение имеет вид ![]() ). Справа показана неустойчивость для начальных значений
). Справа показана неустойчивость для начальных значений ![]() ,
, ![]() ,
, ![]() , не удовлетворяющих уравнению прямой
, не удовлетворяющих уравнению прямой ![]() (решение имеет вид
(решение имеет вид ![]() ).
).
Случай 4. Вершина![]() :
: ![]()
![]()
![]() .
.
Общее решение уравнения (1) имеет вид ![]() .
.
Зададим начальные условия ![]() . Тогда, решая систему
. Тогда, решая систему
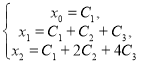
относительно ![]() , получаем
, получаем ![]()
![]() ,
, ![]() . Для ограниченности решений в этом случае необходимо и достаточно, чтобы
. Для ограниченности решений в этом случае необходимо и достаточно, чтобы ![]() и
и ![]() . В пространстве начальных значений
. В пространстве начальных значений ![]() эти уравнения задают прямую
эти уравнения задают прямую ![]() . Каноническое уравнение прямой имеет вид
. Каноническое уравнение прямой имеет вид ![]() .
.
Получаем следующее
Утверждение 4. Уравнение (1) условно устойчиво в критическом случае ![]()
![]()
![]() тогда и только тогда, когда начальные условия уравнения (1) принадлежат подпространству
тогда и только тогда, когда начальные условия уравнения (1) принадлежат подпространству ![]() .
.
В случае условной устойчивости каждое решение уравнения (1) имеет вид ![]() : все решения являются постоянными (см. пример на рис. 3).
: все решения являются постоянными (см. пример на рис. 3).
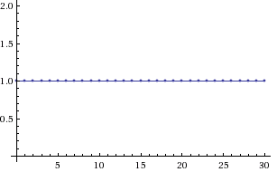
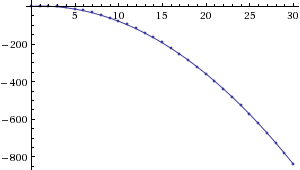
Рис. 4. Примеры решений с начальными условиями, удовлетворяющими (слева) и не удовлетворяющими (справа) уравнению прямой ![]()
На рисунке 4 слева показана условная устойчивость для начальных значений ![]()
![]() ,
, ![]() , удовлетворяющих уравнению прямой
, удовлетворяющих уравнению прямой ![]() (решение имеет вид
(решение имеет вид ![]() ). Справа показана неустойчивость для начальных значений
). Справа показана неустойчивость для начальных значений ![]() ,
, ![]() ,
, ![]() , не удовлетворяющих уравнению прямой
, не удовлетворяющих уравнению прямой ![]() (решение имеет вид
(решение имеет вид ![]() ).
).
Случай 5. Ребро AB: ![]() .
.
Общее решение уравнения (1) имеет вид ![]() .
.
Зададим начальные условия ![]() . Тогда, решая систему
. Тогда, решая систему
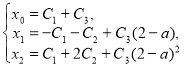
относительно ![]() , получаем
, получаем ![]() ,
, ![]() ,
, ![]() . Для ограниченности решений в этом случае необходимо и достаточно, чтобы
. Для ограниченности решений в этом случае необходимо и достаточно, чтобы ![]() . В пространстве начальных значений
. В пространстве начальных значений ![]() для каждого
для каждого ![]() уравнение
уравнение ![]() задает плоскость
задает плоскость ![]() . Получаем следующее
. Получаем следующее
Утверждение 5. Уравнение (1) условно устойчиво в критическом случае ![]() тогда и только тогда, когда начальные условия уравнения (1) принадлежат подпространству
тогда и только тогда, когда начальные условия уравнения (1) принадлежат подпространству ![]() .
.
В случае условной устойчивости каждое решение уравнения (1) имеет вид ![]() и обладает свойством:
и обладает свойством: ![]() ,
, ![]() Если дополнительно
Если дополнительно![]() , то
, то ![]() .
.
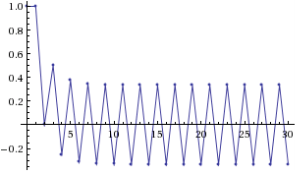
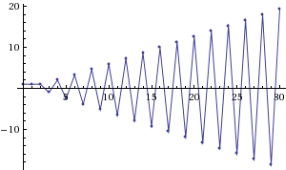
Рис. 5. Примеры решений с начальными условиями, удовлетворяющими (слева) и не удовлетворяющими (справа) уравнению плоскости β
На рисунке 5 слева показана условная устойчивость при ![]() для начальных значений
для начальных значений ![]() ,
, ![]() ,
, ![]() , удовлетворяющих уравнению плоскости
, удовлетворяющих уравнению плоскости ![]() (решение имеет вид
(решение имеет вид ![]() ). Справа показана неустойчивость при
). Справа показана неустойчивость при ![]() для начальных значений
для начальных значений ![]() ,
, ![]() ,
, ![]() , не удовлетворяющих уравнению плоскости
, не удовлетворяющих уравнению плоскости ![]() (решение имеет вид
(решение имеет вид ![]() ).
).
Случай 6. Ребро CD: ![]() .
.
Общее решение уравнения (1) имеет вид ![]() .
.
Зададим начальные условия ![]() . Тогда, решая систему
. Тогда, решая систему
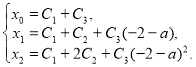
относительно ![]() , получаем
, получаем ![]() ,
, ![]() ,
, ![]() . Для ограниченности решений в этом случае необходимо и достаточно, чтобы
. Для ограниченности решений в этом случае необходимо и достаточно, чтобы ![]() . Получаем следующее
. Получаем следующее
Утверждение 6. Уравнение (1) условно устойчиво в критическом случае ![]() тогда и только тогда, когданачальные условия уравнения (1) принадлежат подпространству
тогда и только тогда, когданачальные условия уравнения (1) принадлежат подпространству ![]() .
.
В пространстве начальных значений ![]() для каждого
для каждого ![]() уравнение
уравнение ![]() задает плоскость
задает плоскость ![]() . В случае условной устойчивости каждое решение уравнения (1) имеет вид
. В случае условной устойчивости каждое решение уравнения (1) имеет вид ![]() и обладает свойством:
и обладает свойством: ![]() .
.
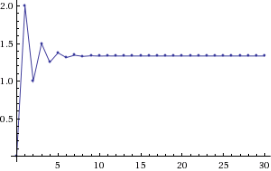
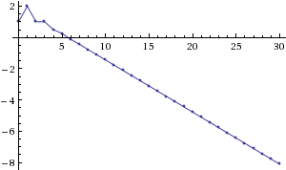
Рис. 6. Примеры решений с начальными условиями, удовлетворяющими (слева) и не удовлетворяющими (справа) уравнению плоскости γ
На рисунке 6 слева показана условная устойчивость при ![]() для начальных значений
для начальных значений ![]() ,
, ![]() ,
, ![]() , удовлетворяющих уравнению плоскости
, удовлетворяющих уравнению плоскости ![]() (решение имеет вид
(решение имеет вид ![]() ). Справа показана неустойчивость при
). Справа показана неустойчивость при ![]() для начальных значений
для начальных значений ![]() ,
, ![]() ,
, ![]() , не удовлетворяющих уравнению плоскости
, не удовлетворяющих уравнению плоскости ![]() (решение имеет вид
(решение имеет вид ![]() ).
).
Сравнение подпространств начальных условий
Проведем сравнение подпространств начальных условий для всех рассмотренных критических случаев, используя их геометрическую интерпретацию. Список всех критических случаев и соответствующих им подпространств приведен в следующей таблице.
|
Критический случай (граничные точки) |
Геометрическая интерпретация подпространства начальных условий |
|
|
Плоскость |
|
|
Прямая |
|
|
Прямая |
|
AB: |
Плоскость |
|
CD: |
Плоскость |
Заметим, что все полученные прямые и плоскости проходят через точку ![]() .
.
Выясним взаимное расположение плоскостей ![]() ,
, ![]() ,
, ![]() и прямых
и прямых ![]() ,
, ![]() .
.
-
Плоскость
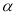 пересекает
пересекает 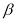 по прямой
по прямой 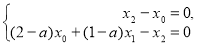 , каноническое уравнение которой
, каноническое уравнение которой 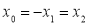 , т. е.
, т. е. 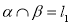 . Заметим, что при
. Заметим, что при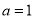 имеем
имеем 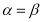 .
.
-
Плоскость
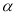 пересекает
пересекает 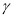 по прямой
по прямой 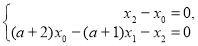 , каноническое уравнение которой
, каноническое уравнение которой 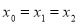 , т. е.
, т. е. 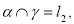 . Заметим, чтопри
. Заметим, чтопри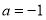 имеем
имеем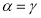 .
.
-
Рассмотрим прямую
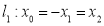 и плоскость
и плоскость 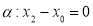 . Они имеют общую точку и скалярное произведение направляющего вектора прямой на вектор нормали к плоскости равно нулю. Значит
. Они имеют общую точку и скалярное произведение направляющего вектора прямой на вектор нормали к плоскости равно нулю. Значит 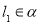 .
.
-
Рассмотрим прямую
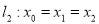 и плоскость
и плоскость 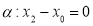 . Они имеют общую точку и скалярное произведение направляющего вектора прямой на вектор нормали к плоскости равно нулю. Значит
. Они имеют общую точку и скалярное произведение направляющего вектора прямой на вектор нормали к плоскости равно нулю. Значит 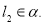
-
Рассмотрим плоскости
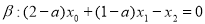 и
и 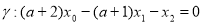 . Координаты векторов нормали к плоскостям не пропорциональны, поэтому плоскость
. Координаты векторов нормали к плоскостям не пропорциональны, поэтому плоскость 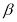 пересекает
пересекает 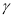 по прямой
по прямой 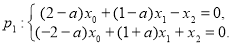 Прямая
Прямая 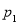 проходит через точку
проходит через точку 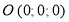 , следовательно, ее каноническое уравнение имеет вид:
, следовательно, ее каноническое уравнение имеет вид: 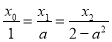 .
.
-
Рассмотрим прямую
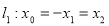 и плоскость
и плоскость 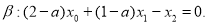 Они имеют общую точку и скалярное произведение направляющего вектора прямой на вектор нормали к плоскости равно нулю. Значит
Они имеют общую точку и скалярное произведение направляющего вектора прямой на вектор нормали к плоскости равно нулю. Значит 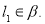
-
Рассмотрим прямую
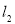 и плоскость
и плоскость 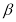 . При
. При 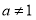 они пересекаются в точке
они пересекаются в точке 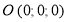 . Если
. Если 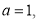 то
то 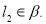
-
Рассмотрим прямую
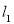 и плоскость
и плоскость 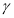 . При
. При 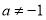 они пересекаются в точке
они пересекаются в точке 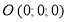 . Если
. Если 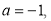 то
то 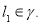
-
Рассмотрим прямую
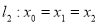 и плоскость
и плоскость  Они имеют общую точку и скалярное произведение направляющего вектора прямой на вектор нормали к плоскости равно нулю. Значит
Они имеют общую точку и скалярное произведение направляющего вектора прямой на вектор нормали к плоскости равно нулю. Значит 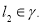
-
Рассмотрим прямые
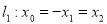 и
и 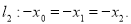 Координаты их направляющих векторов не пропорциональны, значит
Координаты их направляющих векторов не пропорциональны, значит 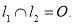
На рисунке 7 изображено взаимное расположение прямых и плоскостей, где ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
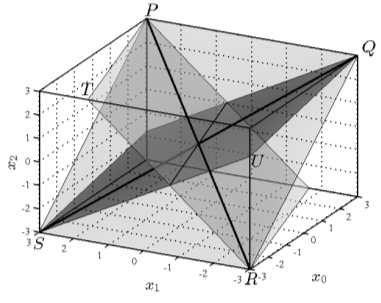
Рис. 7. Взаимное расположение плоскостей ![]() (PQRS),
(PQRS), ![]() (QSU),
(QSU), ![]() (PTR) и прямых
(PTR) и прямых ![]() (QS),
(QS), ![]() (PR).
(PR).
Выводы
Для всех критических случаев подпространства начальных условий, относительно которых уравнение (1) условно устойчиво, имеет размерность 1 или 2. Причем размерность 1 получается только для граничных точек ![]() и
и ![]() . В остальных случаях подпространство начальных условий имеет размерность 2. В общем случае пересечение любой пары подпространств имеет размерность 1, при этом имеют место равенства:
. В остальных случаях подпространство начальных условий имеет размерность 2. В общем случае пересечение любой пары подпространств имеет размерность 1, при этом имеют место равенства: ![]() ,
, ![]() .
.
Работа поддержана грантом ЮУрГГПУ и КГПУ им. В. П. Астафьева (проект № 16–1022).
Литература:
- Diblík, J.; Halfarová, H.; Šafařík, J. Conditional Stability of Weakly Delayed Planar Linear Discrete Systems.Recent Advances in Mathematical and Computational Methods.Proceedings of the 17th International Conference on Mathematics and Computers in Science and Engineering (MACMESE '15). KualaLumpur, Malaysia: WSEASPress, 2015. — P. 111–117.
- ParhiN., Tripathy A. K. On the behavior of solutions of a class third order difference equations // Journal of Difference Equations and Applications. — 2002. — V. 8, No. 5. — P. 415–426.
- Нигматулин Р. М., Кипнис М. М. Свойства дискретных систем третьего порядка на границе их областей устойчивости // Фундаментальные исследования. — 2015. — № 9–1.– С. 39–43; URL: http://www.fundamental-research.ru/ru/article/view?id=38962 (дата обращения: 20.10.2016)
- Чудинов К. М. Частичная и условная устойчивость линейных функционально-дифференциальных уравнений: диссертация... канд. физ.-мат. наук: 01.01.02.- Пермь, 2005.- 98 с.

