Эффективные методы расчета спектральных задач для самосопряженных операторов



В статье обсуждается теория самосопряженных операторов. Описаны основные определения самосопряженных операторов, их связь с нормальными операторами и спектральные свойства.

Кроме того, были рассмотрены классификация самосопряженных операторов и понятия функционального исчисления.

Ключевые слова: самосопряженные операторы, спектральная функция.

Самосопряженные операторы

Если для оператора A выполняется равенство , то этот оператор называется самосопряженным оператором.

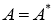
Любой нормальный оператор с действительным спектром является самосопряженным оператором, и наоборот, самосопряженный оператор A является нормальным и его спектр равен .

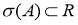
Из определения оператора следует, что оператор

является самосопряженным тогда и только тогда, когда для любого

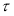
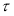
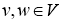
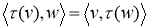
Некоторые свойства сопряженных операторов:

Теорема 1. Пусть V — предгильбертово пространство и

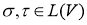
1. Если и самосопряженные, то также самосопряжен.
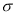
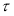
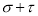
2. Если самосопряжен и действительно, то будет самосопряженным.
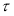
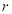
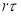
3. Если и самосопряженные, то будет самосопряженным. Тогда и только тогда, выполняется . Учитывая, что , получаем следующее: .
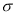
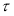
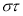
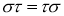
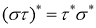
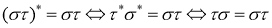
4. Если является самосопряженным, то также будет самосопряженным. Учитывая, что , получаем следующее:

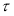
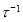
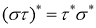
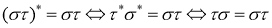
Теорема 2. Пусть V — предгильбертово пространство

1. Если самосопряжен, то для любого действительно.
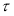
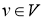
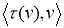
2. Если V комплексное и действительное для любого , то самосопряжен.
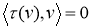
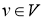
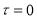
3. Если самосопряжен и для любого , то .
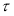
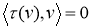
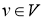
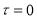
4. Если самосопряжен и , то для любого k>0 .
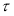
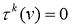
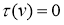
5. Если самосопряжен, то все корни характеристического многочлена (а также минимального многочлена) являются действительными.
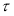
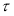
6. Если , имеют различные собственные значения самосопряженного оператора , то .

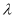
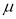
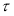
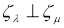
1) Для (1) мы знаем, что

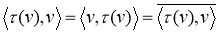
Поэтому должно быть действительным.

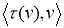
2) Доказать (2)

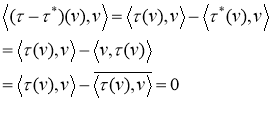
Отсюда следует, что , а это значит, что является самосопряженным.

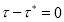
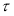
3)

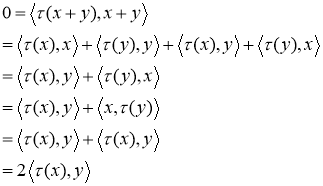
Поэтому .

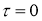
4) Если для любого существует , то для любого m существует . Следовательно,

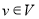
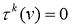
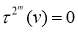
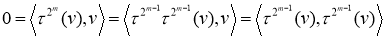
Поэтому . Повторяя этот процесс, мы получаем .

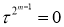
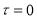
5) Сначала предположим, что V — комплексное векторное пространство, а — корень . Тогда, для любых выполняется и

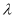
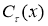
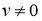
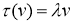
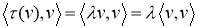
И

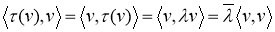
Поэтому

, это значит действительно.

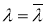
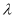
6) Предположим, и , где . Тогда

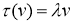
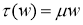
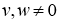
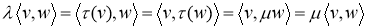
Поэтому , а это означает .

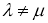
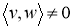
Очевидно, тот факт, что собственные значения самосопряженного оператора являются действительными, означает, что минимальный многочлен распределен по произведениям линейных множителей.

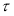
Пусть оператор A является самосопряженным оператором, классифицированным в форме , тогда выполняется для спектров. Таким образом, для любого мы можем определить ортопроекцию из H:

(1.1)

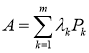
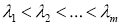
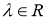
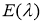
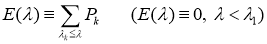
Если использовать формулу функционального уравнения (1.1) для определенного ортопроектора, то выполняется равенство

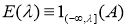
и выводится форма функционального уравнения ортопроектора.

Заключение

В статье рассматриваются основные аспекты теории самосопряженных операторов. Всесторонне изучены определение самосопряженных операторов, их связь с нормальными операторами, спектральные свойства и функциональные характеристики.

Результаты работы позволяют глубже понять свойства операторов и демонстрируют широкую сферу их применения.

Литература:

1. Трунов Н. В. Спектральная теорема. Казань : Издательство Казанского университета, 1989. — 76 с.
2. Бирман М. Ш., Соломяк М. З. Спектральная теория самосопряженных операторов в гильбертовом пространстве. — Л. : Изд-во ЛГУ. 1980. — 264 с.
3. Roman S. (1992) The Spectral Theorem for Normal Operators. In: Advanced Linear Algebra. Graduate Texts in Mathematics, vol 135. Springer, New York