Периодические решения разностного уравнения третьего порядка
Баранова Анастасия Яковлевна, студент;
Шенмаер Ирина Владимировна, студент;
Нигматулин Равиль Михайлович, кандидат физико-математических наук, доцент
Южно-Уральский государственный гуманитарно-педагогический университет (г. Челябинск)
В статье проведено полное исследование периодичности решений линейного разностного уравнения третьего порядка. Указаны все возможные значения коэффициентов, при которых каждое решение уравнения является либо чисто периодическим, либо предельным циклом.
Ключевые слова: разностное уравнение третьего порядка, периодические решения, циклы, предельные циклы
Введение ипостановка задачи
Исследованиеасимптотического поведения решений линейного разностного уравнения третьего порядка
,(1)
где
детально проводилось в [1, 3, 5]. В работе [1] получены условия осциллируемости (колебательности) решений уравнения (1) в виде неравенств — ограничений на коэффициенты уравнения. В работе [5] полностью описана область асимптотической устойчивости уравнения (1) и поведение решений этого уравнения на границе области.
Сформулируем необходимые определения.
Определение 1. Решение 
уравнения (1) называется периодическим с периодом 
(k-циклом или k-периодическим), если для всех 
Определение 2. Решение уравнения (1) называется предельным k-циклом, если существуют последовательности 
и 
такие, что — k-периодическая, 
и для всех 
Известно [4], что периодические решения возникают на границе области асимптотической устойчивости. Для периодичности всех решений уравнения (1) необходимо, чтобы характеристический многочлен уравнения (1)
имел простые комплексно сопряженные корни, по модулю равные 1 или простой действительный корень 
.
Используя результаты работы [5], в этой статье мы описываем все возможные значения коэффициентов уравнения (1), при которых каждое решение является либо чисто периодическим, либо предельным циклом.
Основные результаты
Случай 1. Коэффициенты уравнения (1) удовлетворяют системе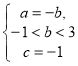 
.
Общее решение уравнения (1) имеет вид 
.
Зададим начальные условия
. Тогда, решая систему
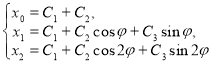
относительно 
, получаем:
В этом случае характеристический многочлен можно представить в виде
.
При 
многочлен 
имеет два комплексно сопряженных корня: 
таких, что 
.
Преобразуем решение 
, применив метод введения вспомогательного угла. Получим 
, где 
.
Введем величину 
Решение уравнения (1) является k-периодическим тогда и только тогда, когда 
. Получаем, что 
Это равенство выполняется для всеx 
тогда и только тогда, когда 
. Получаем следующее
Утверждение 1. Если коэффициенты
уравнения (1) удовлетворяют системе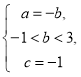 
то все решения уравнения (1) являются периодическими тогда и только тогда, когда 
, где 
.
Замечание. Если 
, т. е. начальные условия удовлетворяют равенствам 
, то решение имеет вид 
.
Случай 2. Коэффициенты уравнения (1) удовлетворяют системе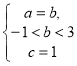 
.
Общее решение уравнения (1) имеет вид 
.
Зададим начальные условия 
. Тогда, решая систему
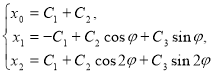
относительно 
, получаем:
В этом случае характеристический многочлен можно представить в виде
.
При 
многочлен 
имеет два комплексно сопряженных корня: 
таких, что 
.
Преобразуем решение
, применив метод вспомогательного угла. Получим 
, где . Тогда 
Равенство возможно только при четном k и 
. Получаем следующее
Утверждение 2. Если коэффициенты уравнения (1) удовлетворяют системе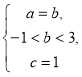 
то все решения уравнения (1) являются периодическими с четным периодом тогда и только тогда, когда , где 
.
Замечание. Если 
, т. е. начальные условия удовлетворяют равенству 
, то решение имеет вид 
и является периодическим, с периодом 2.
Случай 3. Коэффициенты уравнения (1) удовлетворяют системе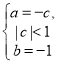 
.
Общее решение уравнения (1) имеет вид 
. Очевидно, что в общем случае все решения уравнения (1) являются предельными 2-циклами (здесь 
где 
— 2-цикл, 
, 
).
Случай 4. Коэффициенты уравнения (1) удовлетворяют системе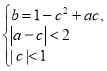 
.
Общее решение уравнения (1) имеет вид 
. Характеристический полином 
имеет следующие корни: действительный корень 
, 
, пару комплексно сопряженных корней 
, 
, 
, 
.
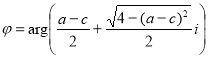В этом случае получаем следующее
Утверждение 3. Если коэффициенты уравнения (1) удовлетворяют системе 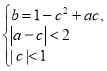, то все решения уравнения (1) являются предельными циклами тогда и только тогда, когда , где , .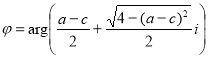
Работа поддержана грантом ЮУрГГПУ и КГПУ им. В. П. Астафьева (проект № 16–1022).
Литература:
- Parhi N., Tripathy A. K. On the behavior of solutions of a class third order difference equations // Journal of Difference Equations and Applications. — 2002. — V. 8, No. 5. — P. 415–426.
- Schmeidel E. L., Janglajew K. R. Periodicity of solutions of nonhomogeneous linear difference equations // Advances in Difference Equations. — 2012. — 2012:195. URL:https://advancesindifferenceequations.springeropen.com/articles/10.1186/1687–1847–2012–195. doi:10.1186/1687–1847–2012–195. (дата обращения: 10.12.2016)
- Баранова А. Я., Шенмаер И. В., Нигматулин Р. М. Условная устойчивость разностного уравнения третьего порядка в критических случаях // Молодой ученый. — 2016. — № 25(129). — С. 113–122.
- Козак А. Д., Новоселов О. Н. Асимптотическое поведение решений линейного однородного разностного уравнения второго порядка // Математические заметки. — 1999. — Т. 66, Вып. 2. — С. 211–215.
- Нигматулин Р. М., Кипнис М. М. Свойства дискретных систем третьего порядка на границе их областей устойчивости // Фундаментальные исследования. — 2015. — № 9–1. — С. 39–43; URL: http://www.fundamental-research.ru/ru/article/view?id=38962 (дата обращения: 10.12.2016).
