В данной работе рассматривается применение проекционных операторов при разрешении задачи синтеза локально оптимальных управлений объектом, структуру которого можно охарактеризовать наличием нелинейности. В основе рассматриваемой методики лежат проекторы, позволяющие отобразить рассматриваемую задачу синтеза на линейное многообразие и упростить ее разрешение.
Ключевые слова: задача Коши, локально оптимальное управление, нелинейность, проекционный оператор, функция оптимальности.
Пусть математическая модель объекта управления определена на основе нелинейных разностных уравнений с гладкой правой частью вида (1):
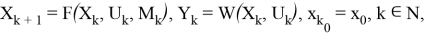
где
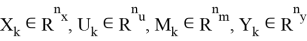
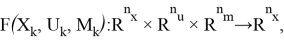
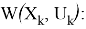
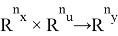
При осуществлении синтеза оптимальных управлений для объекта, описываемого уравнением (1), необходимо использовать кусочно-линейные уравнения для учета типовых нелинейностей, подробно описываемые в работе [3]. Тогда объект управления типа (1) можно описать в виде задачи Коши для кусочно-линейных разностных уравнений согласно формуле (2):
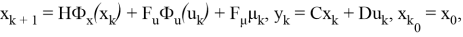
где
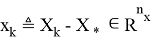
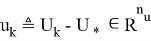
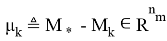
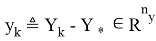
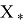
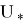
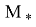
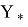
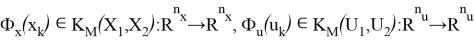
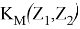
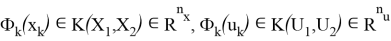
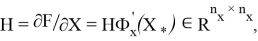
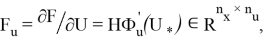
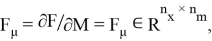
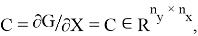
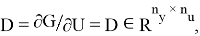
соответствуют матрицам Якоби в точках
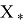
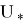
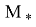
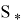
Стоит отметить, что локально оптимальные ограниченные (ЛОУ)
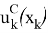
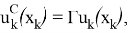
где
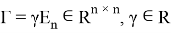
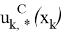
На основе применения проекционных операторов ЛОУ можно представить управления
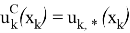
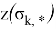
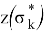
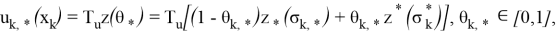
где
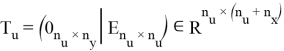
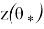
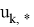
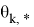
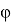
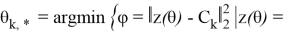
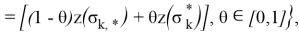
где
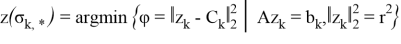
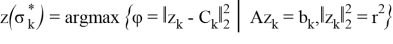
Таким образом, на основе уравнений (5), (6) можно сформировать векторы управлений с обратной связью по состоянию
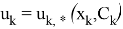
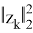
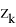
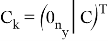
Далее требуется задать «множества моделей», которые позволяют учесть нелинейности уравнений объекта типа (2) по координатам состояний
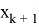
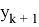
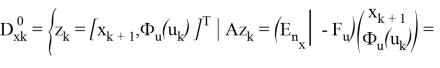
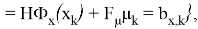
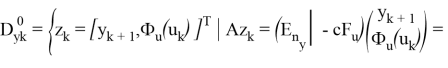
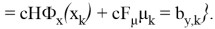
«Множества ограничений» — множества неравенств, ограничивающих расширенные векторы
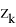
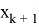
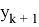
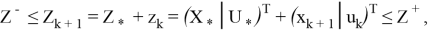
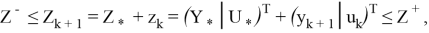
где
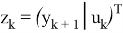
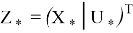
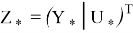
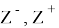
Таким образом, базовые задачи позволяют оптимальные управления, позволяющие минимизировать функционал качества, определяемый евклидовой нормой отклонений вектора
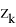
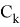
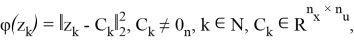
для статического закона c соответствующими множествами «моделей» (7) и «ограничений» (8), имеют вид (10):
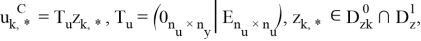
где управления
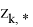
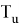
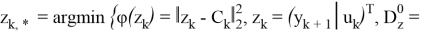
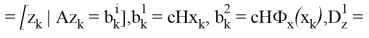
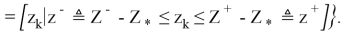
Задачи класса (11) можно разрешить с использованием проекционных операторов конечномерной минимизации. Следующим шагом является аппроксимация задач типа (10). Эллипсоиды ограничений аппроксимируют параллелепипед, причем область ограничений для векторов
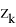
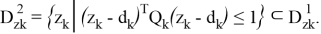
Центр и полуоси эллипсоидов определяются согласно соотношениям (13):
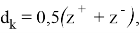
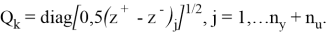
Для случая, когда матрицы
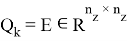
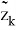
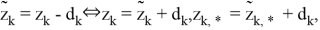
причем эллипсоид преобразуется в шар.
С учетом этого соотношения для определения статических ЛОУ потребуется разрешить базовые задачи вида (15):
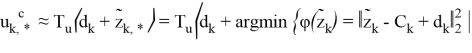
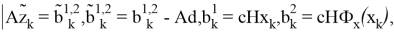
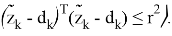
Таким образом, на основе уравнений (15) можно сформулировать разностные операторы, характеризующие замкнутые системы, согласно соотношениям (16):
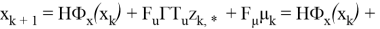
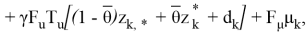
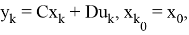
где
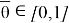
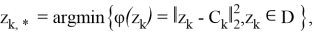
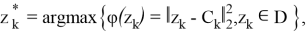
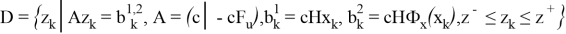
Разностные операторы систем локально оптимального управления на основе (1), (3), (16) и (17) определяют задачу Коши:
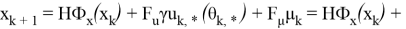
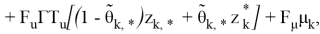
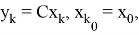
с зависящей от координат состояния «функцией оптимальности»
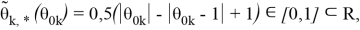
где
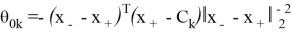
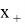
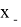
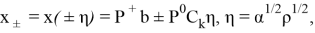
где
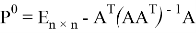
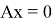
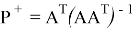
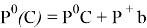
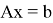
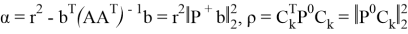
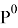
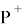
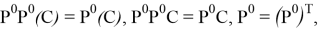
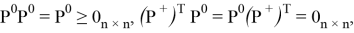
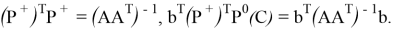
Данный проектор позволяет вычислить функцию оптимальности
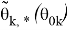
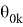
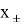
Таким образом, были построены математические модели замкнутых локально оптимальных систем, описываемые уравнениями (17) и (18). Успешный синтез системы, в свою очередь, приводит к задаче осуществления анализа устойчивости синтезированной системы. Провести данный анализ можно, например, с использованием метода сжимающих отображений, что представлено в работах [3], [4].
Литература:
1. Козлов В. Н. Негладкие системы, операторы оптимизации и устойчивость энергообъединений. — СПб.: Изд-во Политехн. ун-та, 2017. — 177 с.
2. Козлов В. Н. Проекционный метод оптимизации оптимальных ограниченных управлений динамических систем. — СПб: Издательско-полиграфическая ассоциация высших учебных заведений, 2018. — 190 с.
3. Козлов В. Н. Проекционный метод синтеза ограниченных оптимальных управлений динамических систем энергетики. — СПб: ПОЛИТЕХ-ПРЕСС, 2019. — 165 с.
4. Козлов В. Н. Системный анализ, оптимизация и принятие решений: учебное пособие / В. Н. Козлов. — М: Проспект, 2014. — 173 c.

