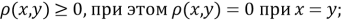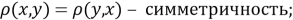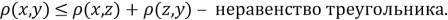В статье сформированы примеры функций со специальными свойствами для синтеза новых метрик в метрических пространствах.
Ключевые слова: метрика, метрическое пространство, аксиома, неубывающая функция, производная, интеграл.
Как и многие структуры абстрактной математики, понятие метрики в метрических пространствах относится к простому геометрическому понятию — расстоянию между двумя точками
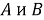
Множество
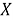
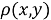
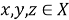
Элементы метрического пространства называют также
точками
, функцию
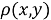
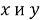
Перечисленные аксиомы согласуются с привычным представлением о свойствах расстояния. Аксиома 3 имеет существенное значение, когда точки
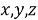
Для создания новых метрик используем специальные неубывающие функции
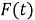
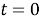
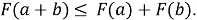
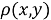
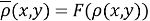
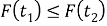
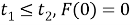
Рассмотрим свойство производной
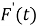
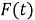
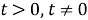
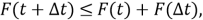
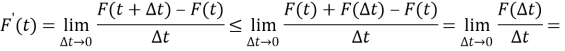
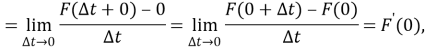
т. е. при
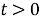
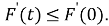
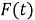
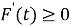
В целом
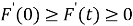
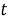
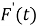
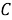
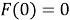
Проверим выполнение аксиом метрики для функции
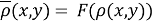
-
Функция
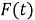
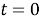
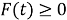
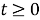
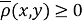
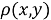
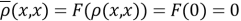
-
Проверка симметричности
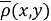
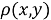
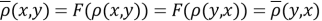
-
Проверка неравенства треугольника для
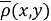
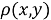
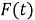
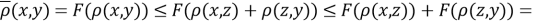
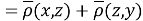
Далее представлен графический анализ неубывающих функций
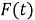
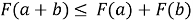
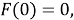
Проверка свойства
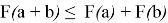
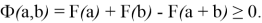
В качестве производной первой функции выберем функцию вида
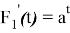
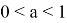
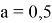
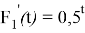
Находим неопределённый интеграл от
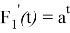
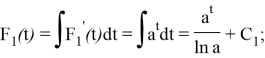
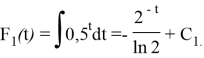
Значение константы интегрирования
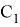
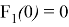
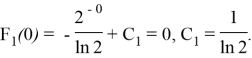
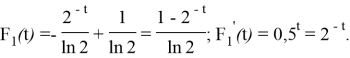
Графики функций
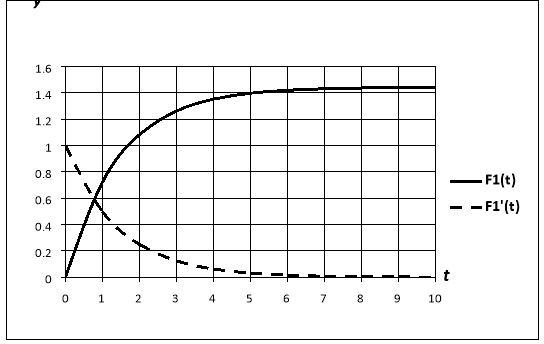
Рис. 1. График функции
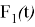
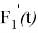
Докажем аналитически выполнение свойства
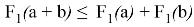
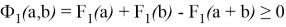
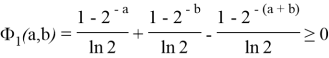
или
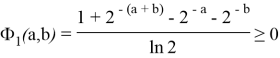
При этом
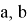
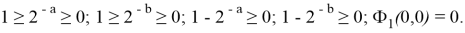
Рассмотрим
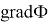
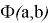
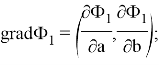
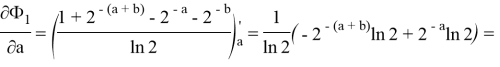
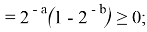
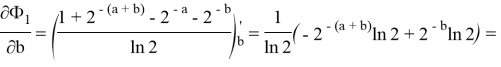
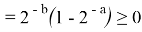
Из положительности компонент вектора градиента делаем вывод, что при любых значениях
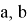
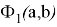
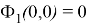
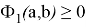
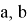
Таким образом, функцию
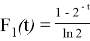
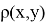
если
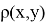
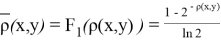
В качестве производной второй функции выберем дробно-иррациональную функцию вида
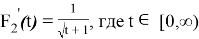
Находим неопределённый интеграл от
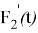
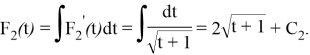
Подберем константу интегрирования
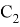
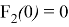
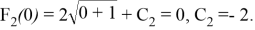
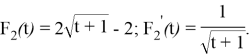
Графики функций
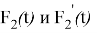
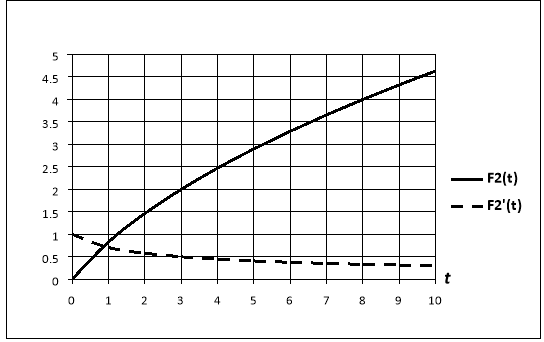
Рис. 2. График функции
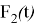
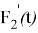
Докажем аналитически выполнение свойства
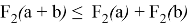
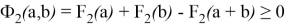
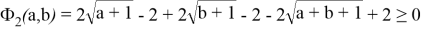
или
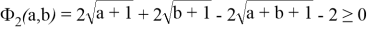
При этом
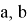
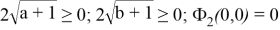
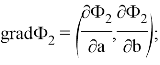
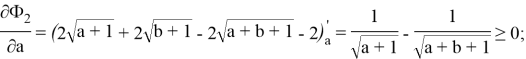
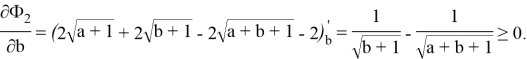
Также как и в первом примере из положительности компонент вектора градиента делаем вывод, что при любых значениях
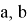
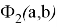
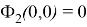
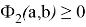
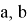
Таким образом, функцию
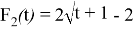
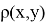
если
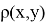
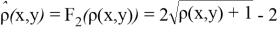
Для третьего примера возьмем убывающую и повсюду положительную дробно-рациональную функцию вида
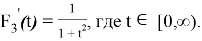
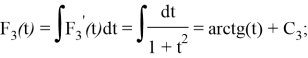
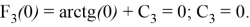
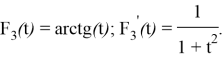
Графики функций
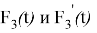
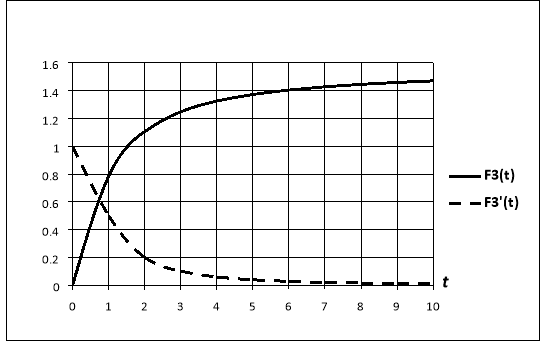
Рис. 3. График функции
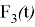
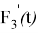
Докажем выполнение свойства
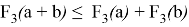
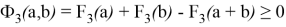
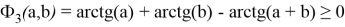
При этом
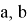
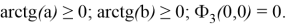
На рис. 4 представлен график функции двух переменных
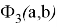
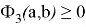
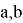
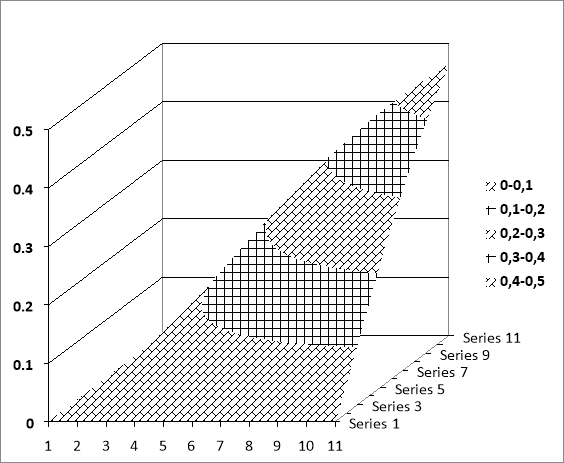
Рис. 4. График функции двух переменных
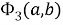
Таким образом, функцию
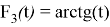
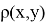
если
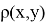
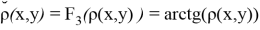
Функции
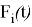
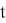
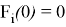
В метрическом пространстве
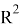
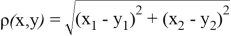
С помощью выбранных функций
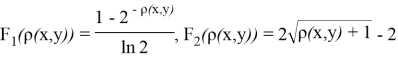
и
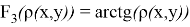
созданы новые метрики на базе евклидовой метрики
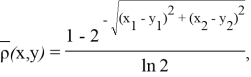
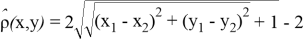
и
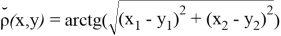
Таким образом, в данной работе построены примеры функций
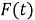
Литература:
1. Филимоненкова, Н. В. Конспект лекций по функциональному анализу: Учебное пособие. — СПб.: Издательство «Лань», 2015. — 176 с.: ил. — (Учебники для вузов. Специальная литература).
2. Колмогоров, А. Н. Элементы теории функций и функционального анализа / А. Н. Колмогоров, С. В. Фомин. — 7-е изд. — М.: Физматлит, 2004. — 572 с.