Метод конхоидального преобразования плоских кривых

Конхоидальным называют такое преобразование кривой линии, при котором радиусы-векторы ее точек, исходящие из заданного полюса, увеличиваются и уменьшаются на одну и ту же величину. Кривые линии, являющиеся конхоидальным преобразованием других линий, называют, конхоидами (греч. напоминающая раковину).

Всякая конхоида состоит из двух ветвей, которые иногда вырождаются в одну кривую линию. На рис. 1 показаны построения конхоиды кривой линии АВ. Через точку О (полюс) проведем пучок лучей, пересекающих кривую АВ. На каждом луче от точки базовой кривой откладываем в обе стороны равные отрезки. Геометрическим местом концов этих отрезков является кривая линия — конхоида исходной кривой АВ относительно данного полюса О. конхоидой окружности относительно центра будет пара окружностей, концентрических базовой окружности и одинаково удаленных от нее.

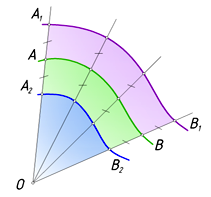
Рис. 1

На рис. 2 представлены конхоиды окружности относительно полюса, лежащего на самой окружности. Такого рода конхоиды называют улитками Паскаля. Пометим на базовой окружности радиуса r точку О и примем ее за полюс окружности откладываем отрезки, равные a=2r. Концами этих отрезков наметится кривая линия называемая кардиоидой.

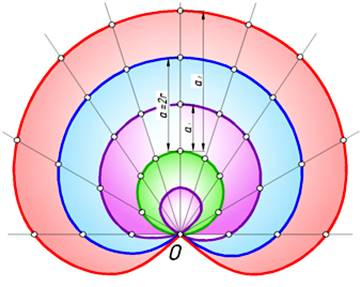
Рис. 2

Задаваясь отрезками а₁ или а₂ меньшими или большими 2 r, получим конхоиды окружности, которые называют укороченными и удлиненными кардиоидами.

Улитку Паскаля широко применяют в технике при конструировании эксцентриков, кулачков у машин, ряда зубчатых колес. Их также широко используют и в оптической технике.

Конхоиды прямой линии называют конхоидами Никомеда, по имени древнегреческого ученого, изучавшего их. На рис.3 показаны различные конхоиды Никомеда одной и той же прямой линии АВ.

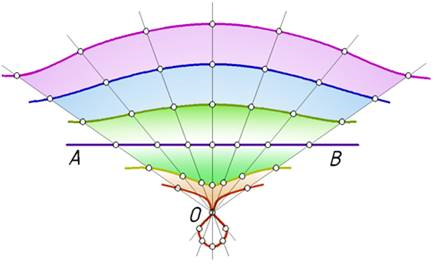
Рис. 3

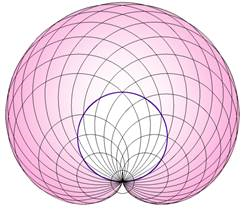
Рис. 4

Имеется очень изящный метод демонстрации кардиоиды к примеру приведенной на рис.4. Она является частным видом эпициклоиды, и при этом радиусы направляющих и движущихся окружностей равны.

Литература:

1.        Бубненников А. В., Громов М. Я. Начертательная геометрия. — Москва: Высшая школа, 1965.

2.        Савелов А. А. Плоские кривые. — Москва. 1960.

3.        Энциклопедический словарь юного математика. — Ташкент. 1992.

4.        Атаджанов Р. К. Методы геометрического построения. — Ташкент: Укитувчи, 1965.

5.        Методы преобразования плоских кривых на основе инцидентности. Магистерская диссертации. — Ташкент. 2010.