Анализ многих задач механики, физики и техники, математической биологии привели к необходимости исследования интегро-дифференциальных уравнений.
Интегро-дифференциальные уравнения применяются к изучению щелевых антенн, изгибов балок на упругих основаниях, в задачах о взаимодействии волн в электролинейных полях, колебаниях твердого тела, имеющего полости, заполненные вязкой жидкостью, колебаниях валов, а также в ряде других задач механики и теории колебаний, где учитывается эффект последействия, описываемый с помощью соответствующих интегралов.
В данной статье рассматривается вопросы построения периодических решений квазилинейных интегро-дифференциальных уравнений в критических случаях выше первого порядка.
Решим уравнение (систему)
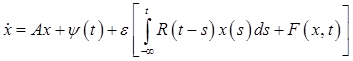 ,
, 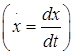 (1)
(1)
где 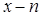 -мерный вектор;
-мерный вектор;
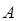 - постоянная
- постоянная 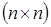 — матрица, обладающая резонансными собственными значениями (равными нулю или целой кратности
— матрица, обладающая резонансными собственными значениями (равными нулю или целой кратности 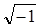 );
);
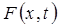 -вектор функция, представима полиномом по
-вектор функция, представима полиномом по 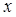 , с коэффициентами
, с коэффициентами 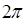 - периодическими функциями по
- периодическими функциями по 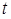 , разложимыми по
, разложимыми по 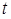 в полином Фурье;
в полином Фурье;
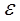 - малый положительный параметр;
- малый положительный параметр;
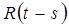 -так называемое ядро релаксации.
-так называемое ядро релаксации.
Линейная однородная система,
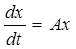 (2)
(2)
соответствующая уравнениям (1), обладает при принятых допущениях о собственных значениях матрицы 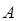 -семейством
-семейством 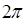 -периодических решений, т. е.
-периодических решений, т. е.
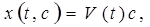 (3)
(3)
где 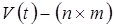 — матрица;
— матрица;
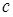 — произвольный постоянный вектор.
— произвольный постоянный вектор.
Предполагаем, что 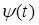 удовлетворяет условию существования
удовлетворяет условию существования 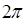 -периодического решения системы (1) при
-периодического решения системы (1) при 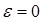 . Тогда при
. Тогда при 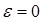 мы получим так называемое порождающееся семейство
мы получим так называемое порождающееся семейство 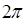 -периодических решений
-периодических решений
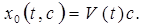 (4)
(4)
Здесь 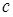 — произвольный вектор.
— произвольный вектор.
Полагаем в (1)
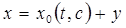 (5)
(5)
и получим для 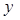 систему
систему
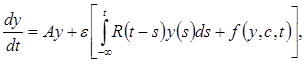 (6)
(6)
где
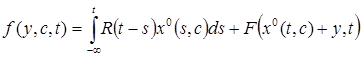 (7)
(7)
Будем искать функцию 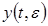 и постоянную
и постоянную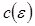 методом итераций, считая, что последовательные приближения
методом итераций, считая, что последовательные приближения 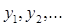 и
и 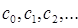 удовлетворяют система
удовлетворяют система
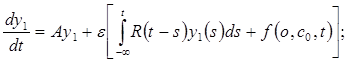 (8)
(8)
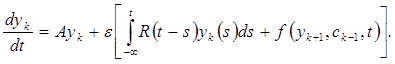 (9)
(9)
При этом будем искать все 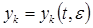 их
их 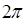 -периодических функций, ортогональные по всем
-периодических функций, ортогональные по всем 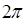 - периодическим решениям однородной системы (2).
- периодическим решениям однородной системы (2).
Рассматриваем сначала систему (8) для первого приближения 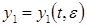 и стараемся удовлетворять, если возможно, условию существования
и стараемся удовлетворять, если возможно, условию существования 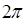 -периодического решения этой системы, т. е. условию, аналогичному
-периодического решения этой системы, т. е. условию, аналогичному 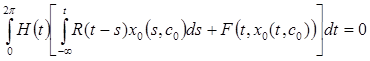
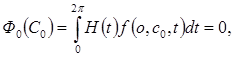 (10)
(10)
где 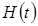 -матрица, сопряженная по отношению к матрице
-матрица, сопряженная по отношению к матрице
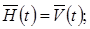
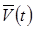 -матрица периодических решений системы, сопряженной к (2)
-матрица периодических решений системы, сопряженной к (2)
Это уравнение относительно постоянного вектора 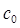 представляющее собой условие существования периодического решения уравнения (8) обращающееся в нуль при
представляющее собой условие существования периодического решения уравнения (8) обращающееся в нуль при 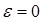 . Если она имеет вещественное решение
. Если она имеет вещественное решение 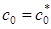 (в случае, когда решение (4) выбирается вещественным), то саму функцию
(в случае, когда решение (4) выбирается вещественным), то саму функцию 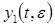 находим как частное
находим как частное 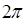 -периодическое решение системы (8), ортогональное семейству (3).
-периодическое решение системы (8), ортогональное семейству (3).
После этого рассматриваем систему для второго приближения 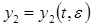 . Условие существования периодического решения этой системы
. Условие существования периодического решения этой системы
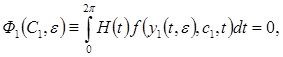 (11)
(11)
является уравнением для определения постоянного вектора 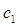 зависящего от параметра
зависящего от параметра 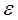 . Если оно имеет вещественное решение
. Если оно имеет вещественное решение 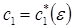 , обращающееся в
, обращающееся в 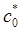 при
при 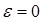 , то
, то 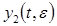 определяем опять как частное
определяем опять как частное 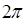 -периодическое решение системы (8) при
-периодическое решение системы (8) при 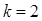 , ортогональное к семейству (3) и т. д.
, ортогональное к семейству (3) и т. д.
Определение. Для системы (1) имеет место критический случай 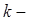 го порядка, если система (8) для
го порядка, если система (8) для 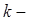 го приближения является первой, для которой условие существования периодического решения, представляющее уравнение относительно постоянного вектора
го приближения является первой, для которой условие существования периодического решения, представляющее уравнение относительно постоянного вектора 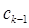 , или не имеет вещественного решения или имеет решение
, или не имеет вещественного решения или имеет решение 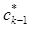 являющееся простым при условии учета соответствующих членов низшего порядка относительно
являющееся простым при условии учета соответствующих членов низшего порядка относительно 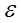 в выражении для
в выражении для
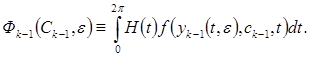
Естественно, что проверка этих условий осуществляется последовательно: сначала при 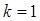 , затем при
, затем при 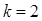 и т. д. Тогда непосредственно и выбираются члены низшего порядка, которые следует учитывать при установлении, является ли решение уравнения для вектора
и т. д. Тогда непосредственно и выбираются члены низшего порядка, которые следует учитывать при установлении, является ли решение уравнения для вектора 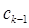 простым.
простым.
При 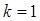 имеет для
имеет для 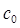 уравнение (10), совпадающее с уравнением порождающих амплитуд
уравнение (10), совпадающее с уравнением порождающих амплитуд 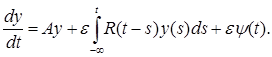
Пусть уравнение (10) имеет решение 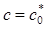 не являющееся простым, т. е. пусть
не являющееся простым, т. е. пусть
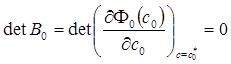 (12)
(12)
Тогда обратная матрица 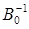 не существует. Это означает, что для системы (8)
не существует. Это означает, что для системы (8) 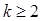 мы не можем гарантировать выбор постоянных векторов
мы не можем гарантировать выбор постоянных векторов 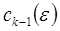 , обращающихся в
, обращающихся в 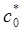 при
при 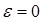 обеспечивающих существование
обеспечивающих существование 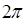 -периодических решений
-периодических решений 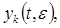
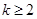 обращающихся в нуль вместе с
обращающихся в нуль вместе с 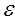 . Действительно, рассмотрим систему (6), представим функцию
. Действительно, рассмотрим систему (6), представим функцию 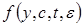 в виде
в виде
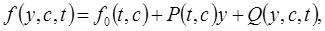 (13)
(13)
где
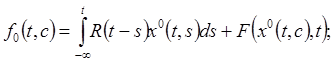
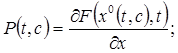 (14)
(14)
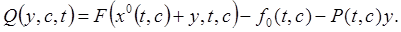
Определив решения 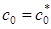 уравнения
уравнения
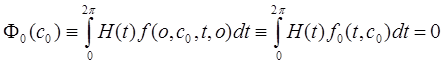 (15)
(15)
найдем из системы (8) первое приближение 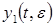 и перейдем к системе для второго приближения, т. е. к системе
и перейдем к системе для второго приближения, т. е. к системе
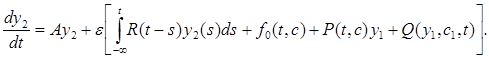 (16)
(16)
Уравнение (11), представляющее условие существования периодического решения этой системы, запишется в виде
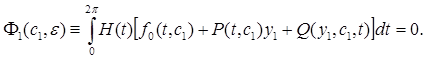 (17)
(17)
При 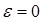 (тогда и
(тогда и 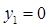 ) это уравнение преобразуется в уравнение (15)
) это уравнение преобразуется в уравнение (15) 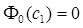 и имеет решение
и имеет решение 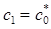 . Однако учитывая условие (12) имеем
. Однако учитывая условие (12) имеем
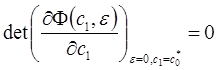
и мы не можем гарантировать при произвольных функциях 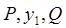 порядка
порядка 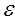 и выше существование решения
и выше существование решения 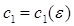 полного уравнения, обращающегося в
полного уравнения, обращающегося в 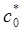 при
при 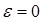 .
.
Возникает вопрос об условиях, гарантирующих существование всех векторов 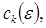
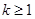 обращающихся в
обращающихся в 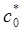 при
при 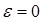 и обеспечивающих существование
и обеспечивающих существование 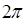 -периодических приближений
-периодических приближений 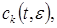
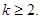
Естественной является случай, когда правой части системы (16), низший порядок членов относительно 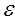 равен единице, если отбросить функцию
равен единице, если отбросить функцию 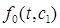 . Такие члены можно получить, если вектор
. Такие члены можно получить, если вектор 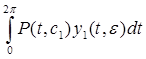 не равен тождественно нулю (так как
не равен тождественно нулю (так как 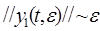 ). Тогда в левой части уравнения (17) при отбрасывании
). Тогда в левой части уравнения (17) при отбрасывании 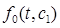 младшие члены относительно
младшие члены относительно 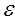 имеют первый порядок, так как функция
имеют первый порядок, так как функция 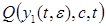 имеет 2- ой порядок относительно
имеет 2- ой порядок относительно 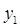
Обозначим
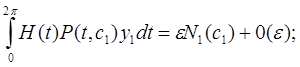 (18)
(18)
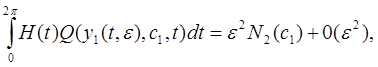 (19)
(19)
где 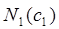 и
и 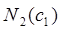 не зависят от
не зависят от 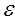
Тогда уравнение (17) перепишется в виде
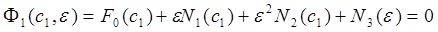 (20)
(20)
где 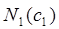 имеет порядок не ниже
имеет порядок не ниже 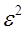
Определение. Простым решением 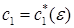 уравнения (17) с учетом членов низшего (или первого) порядка относительно
уравнения (17) с учетом членов низшего (или первого) порядка относительно 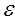 является такое, которое отличается по норме от решения
является такое, которое отличается по норме от решения 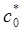 уравнения
уравнения 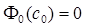 на величину порядка
на величину порядка 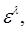 0<
0<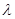 <1 и для которого функциональный определитель
<1 и для которого функциональный определитель
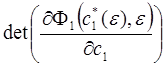 (21)
(21)
будучи отличным от нуля, имеет тот же прядок 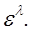
Справедлива следующая теорема, показывающая смысл такого понятия простого решения.
Теорема Пусть функция 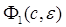 дважды дифференцируема по
дважды дифференцируема по 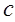 и пусть вместе с уравнением (20) рассматривается другое решение
и пусть вместе с уравнением (20) рассматривается другое решение
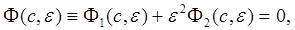 (22)
(22)
левая часть которого отличается от 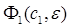 членами порядка
членами порядка 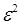 и выше, причем
и выше, причем 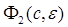 дифференцируемая функция по
дифференцируемая функция по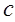 . По
. По 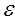 все функции непрерывны.
все функции непрерывны.
Тогда каждому простому решению 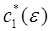 уравнения (20) соответствует единственное решение
уравнения (20) соответствует единственное решение 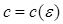 уравнения (22), обращающееся в
уравнения (22), обращающееся в 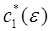 при
при 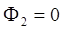 и отличающееся от решения
и отличающееся от решения 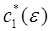 уравнения (20) членами порядка выше
уравнения (20) членами порядка выше 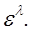 Главные части решения
Главные части решения 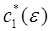 и
и 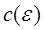 порядка
порядка 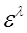 совпадают.
совпадают.
Доказательство. Положим в (22) 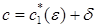 и составим уравнение относительно
и составим уравнение относительно 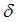 . Разлагая функцию
. Разлагая функцию 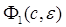 в ряд Тейлора и учитывая, что
в ряд Тейлора и учитывая, что 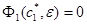
 получим уравнение
получим уравнение
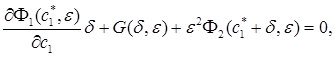 (23)
(23)
где функция 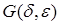 имеет порядок относительно
имеет порядок относительно 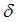 не ниже второго, так как функция
не ниже второго, так как функция 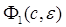 дважды дифференцируемая по
дважды дифференцируемая по 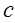 . Если обозначит через
. Если обозначит через 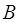 матрицу
матрицу 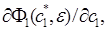 то по условию леммы определитель
то по условию леммы определитель 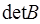 имеет порядок
имеет порядок 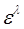 , т. е.
, т. е.
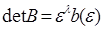
где 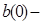 конечное число.
конечное число.
Следовательно, обратная матрица B-1 существует и
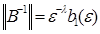
где 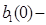 конечное число, в частности,
конечное число, в частности, 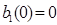 .
.
Перепишем далее (23) в виде
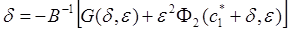 (25)
(25)
и положим 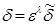 . Учтем, что
. Учтем, что 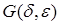 имеет порядок не ниже второго относительно
имеет порядок не ниже второго относительно 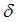 , так что
, так что
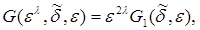
где функции 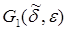 остается непрерывной по
остается непрерывной по 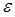 и при
и при 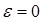 имеет порядок не ниже второго относительно
имеет порядок не ниже второго относительно 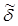 .
.
Следовательно, уравнение для 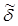 запишется в виде
запишется в виде
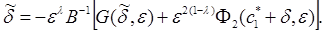 (26)
(26)
Если обозначить 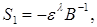 то ввиду (24) норма
то ввиду (24) норма 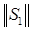 матрицы
матрицы 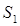 ограничена. Поскольку
ограничена. Поскольку 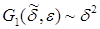 и
и 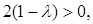 то уравнение (26) запишется также в общем виде
то уравнение (26) запишется также в общем виде
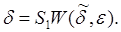 (27)
(27)
Здесь 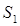 - линейный, ограниченный оператор;
- линейный, ограниченный оператор;
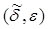 - непрерывная функция
- непрерывная функция 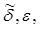 дифференцируемая по
дифференцируемая по 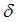 и обращающаяся в нуль вместе с производной
и обращающаяся в нуль вместе с производной 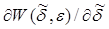 при
при 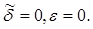
Из [1, 2] следует, что это уравнение имеет в некоторой области 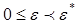 изменения
изменения 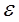 единственное решение
единственное решение 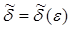 обращается в нуль вместе с
обращается в нуль вместе с 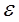 , т. е. вместе с
, т. е. вместе с 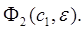
Таким образом, уравнение (2) имеет решение 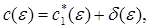 где
где 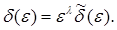 .Это решение удовлетворяет требованиям теоремы.
.Это решение удовлетворяет требованиям теоремы.
Литература:
- Гребенников Е. А.б Рябов Ю. А. Конструктивные методы анализа нелинейных систем. — М., Наука, 1979. — 431 с.
- Лика Д, К., Рябов Ю. А. Методы итераций и мажорирующие уравнения Ляпунова в теории нелинейных колебаний. Кишинев: Штиница, 1974- 291 с.
- Бердиёров А. Ш. Построение периодического решения интегро-дифференциального уравнения типа Вольтера в критическом случае. Деп. ВИНИТИ 03.05.1990 г. № 2380-В90. -10с

