Рассматривается тонкостенная коническая оболочка, у которой отношение толщины h к радиусу кривизны срединной поверхности R2 удовлетворяет условию h<R2/20, а отношение диаметра контура к стреле подъема купола f/d не превышает 1/10. [1, с 43].
Предполагается, что оболочка перемещается только вследствие деформаций сжатия, происходящих лишь в одном меридиональном направлении «рис. 1».. Отрезок меридиана длиной ds после деформирования купола займет новое положение. При этом считается, что деформации в кольцевом направлении отсутствуют.
Проводится линия, изображающая положение меридиана, занятого им после деформирования. Очевидно, что этот участок представляет линейную меридиональную деформацию 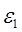 отрезка ds. Величина
отрезка ds. Величина 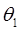 является угловым перемещением отрезка ds. Учитывается, что угол между осью симметрии и радиусом R2 равен углу
является угловым перемещением отрезка ds. Учитывается, что угол между осью симметрии и радиусом R2 равен углу 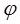
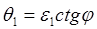 . (1)
. (1)
Угловое перемещение считается положительным по ходу часовой стрелки. Далее предполагается, что оболочка перемещается вследствие только кольцевой деформации сжатия «рис 1», при этом длина меридиана остается неизменной. Отрезок длиной ds после деформирования оболочки займет положение ds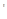 .Проводится линия параллельно положению меридиана, занятому им после деформирования.
.Проводится линия параллельно положению меридиана, занятому им после деформирования.
Длина кольцевого сечения 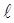 до деформации равна
до деформации равна 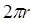 , а после деформации
, а после деформации 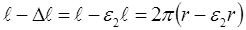 , где
, где 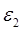 – относительное кольцевое удлинение.
– относительное кольцевое удлинение.
С другой стороны, соотношение между длинами кольца и радиуса после деформирования 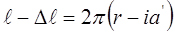 ,
,
где 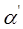 - радиальное перемещение точки.
- радиальное перемещение точки.
Из сравнения полученных выражений находится
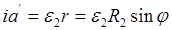 .
. (2)
(2)
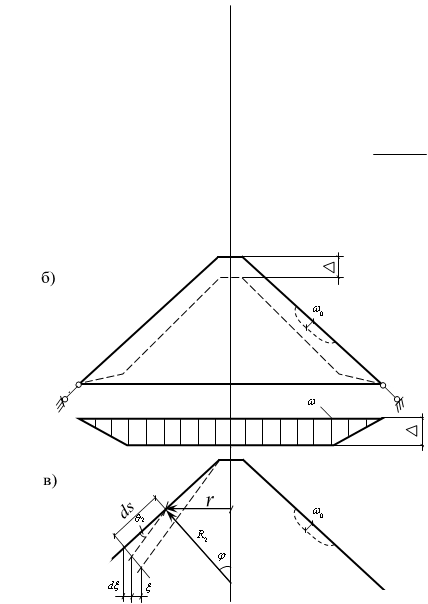
Рис. 1. К определению угловых перемещений оболочки вследствие её деформирования: а,б — в меридиональном направлении при деформируемых и недеформируемых опорных контурах; в- в кольцевом направлении, 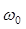 -начальный прогиб
-начальный прогиб
Приращение радиального перемещения на уровне кольцевого сечения, учитывая равенство (2), равно
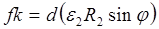 . (3)
. (3)
Выразим угловое меридиональное перемещение (против хода часовой стрелки) 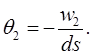 (4)
(4)
Учтем в этом равенстве выражение (3) и (4)
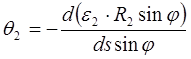 . (5)
. (5)
С учетом (1) и (5) полная величина углового меридионального перемещения

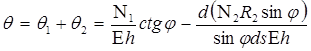 . (6)
. (6)
Уравнения равновесия сил в нормали при подстановке в них значений 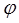 и кривизны деформированной оболочки
и кривизны деформированной оболочки 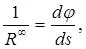
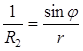 , принимают следующий вид
, принимают следующий вид
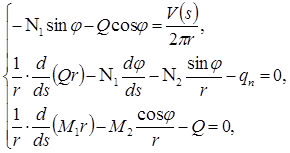 (7)
(7)
где 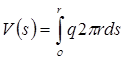 - суммарная осевая нагрузка на часть деформированной оболочки радиуса r; q1, qn и
- суммарная осевая нагрузка на часть деформированной оболочки радиуса r; q1, qn и 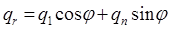 — соответственно меридиональная, нормальная и радиальная нагрузки, отнесенные к единице срединной поверхности оболочек. Если с помощью третьего уравнения (7) исключить поперечную силу первого и второго уравнений (7), то получается два уравнения равновесия, включающего четыре неизвестных силовых фактора (N1, N2, M1 и M2)
— соответственно меридиональная, нормальная и радиальная нагрузки, отнесенные к единице срединной поверхности оболочек. Если с помощью третьего уравнения (7) исключить поперечную силу первого и второго уравнений (7), то получается два уравнения равновесия, включающего четыре неизвестных силовых фактора (N1, N2, M1 и M2)
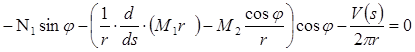 ;
;
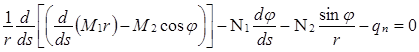 . (8)
. (8)
Уравнения равновесия безмоментной теории получаются, если в уравнениях один и два (7) опустить полученную силу Q=0 или изгибающие моменты М1 и М2=0 в уравнении (8), таким образом можно получить уравнения в виде
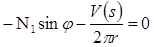 ,
, 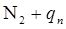
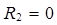 . (9)
. (9)
Если учесть, что
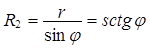 ;
; 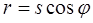 ,
,
то при этом длина образующей s отcчитывается от вершины конуса. С учетом (9) усилия в срединной поверхности купола можно определить по выражениям
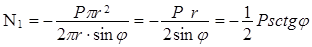 ;
;
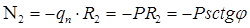 . (10)
. (10)
Усилия N1 и Q выражаются через распорную силу N2 и известные осевые усилия V (s) в сечении оболочки по формулам
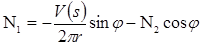 , (11)
, (11)
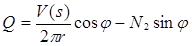 , (12)
, (12)
где N2 = 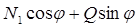 .
.
Усилия N2 и момент М2 выражаются через основные неизвестные по формулам, которые легко получить из уравнений упругости
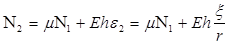 ;
;
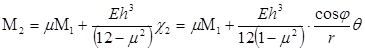 , (13)
, (13)
здесь 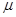 — коэффициент Пуассона определяемый по [29].
— коэффициент Пуассона определяемый по [29].
Силовые факторы (N1, N2, M1 и M2) выражаются с помощью уравнений упругости через деформации срединной поверхности и параметры изменения ее кривизны (ε1,ε2, 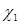 ,
,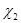 )
)
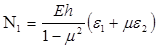 ,
, 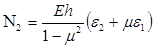 . (14)
. (14)
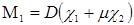 ,
, 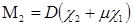 , (15)
, (15)
где 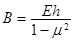 и
и 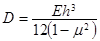 — осевая и цилиндрическая жесткость стенки оболочки
— осевая и цилиндрическая жесткость стенки оболочки 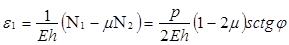 ,
,
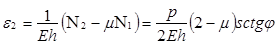 . (16)
. (16)
Максимальные напряжения и деформации возникают у опорного кольца конической оболочки при s=s0.
Определим радиальное перемещение деформированного купола на уровне кольцевого сечения
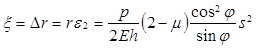 . (17)
. (17)
Угол поворота нормали (6) можно представить
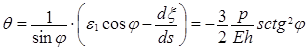 . (18)
. (18)
Вычислим параметры изменения кривизны срединной поверхности оболочки с учетом изменения угла поворота
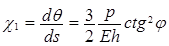 ,
, 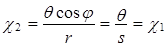 . (19)
. (19)
Максимальные деформации, возникающие в оболочке в связи с её изгибом
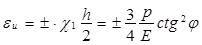 . (20)
. (20)
Сопоставляя эту величину с максимальными деформациями (16), например 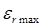 , видим, что их отношение
, видим, что их отношение
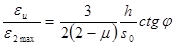 .
.
Это показывает, что погрешность, связанная с игнорированием изгиба, существенна только для очень пологих оболочек, полная высота которых 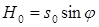 имеет такой же порядок, что и толщина оболочек h (подобно круглой пластине). Для оценки напряженно-деформированного состояния пологих и подъемистых конических оболочек целесообразно применение разрешающего уравнения (11) с учетом влияния краевого эффекта конических оболочек, возникающего вблизи опорного кольца.
имеет такой же порядок, что и толщина оболочек h (подобно круглой пластине). Для оценки напряженно-деформированного состояния пологих и подъемистых конических оболочек целесообразно применение разрешающего уравнения (11) с учетом влияния краевого эффекта конических оболочек, возникающего вблизи опорного кольца.
Литература:
1. Матниязов Б. И., Бердиев О., Раззаков Ж. Железобетонные купола (виды, конструктивные схемы, методы расчета). Т: Фан ва технология, 2009. — 43 с.

