Динамические напряженные деформированные состояния горных пород при воздействии сейсмических волн

Изучение волновых процессов является одной из самых важных и сложных задач в механике деформируемого твердого тела. Это подтверждается тем фактом; что существует весьма ограниченный круг задач, для которых получено аналитическое решение, в отличие от акустики или электродинамики, где эти решения вычисляются достаточно просто. Воспользовавшись принципом возможных перемещений, выпишем вариационное уравнение задачи теории упругости в плоской постановке

Введем в рассмотрение цепные усилия

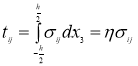
И интегрируя по толщине полосы, приведем (1) к следующему виду:

Интегрируя дважды по частям и приравнивая нулю коэффициенты при вариациях внутри тела или на его границе, получаем следующую систему дифференциальных уравнений в частных производных

С граничными условиями:

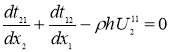
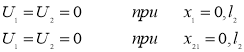
Альтернативными к ним

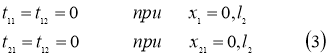
Рассмотрим теперь бесконечную вдоль оси с производным законом изменения толщины . Будем искать решение задачи в виде:

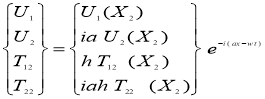
Описывающей планарные гармонические волны, распространяющиеся вдоль оси . Подставляя (4) в (3), получаем систему обыкновенных дифференциальных уравнений первого порядка

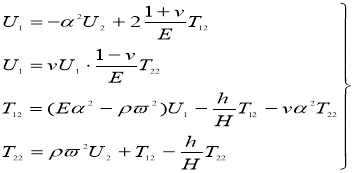
С граничными условиями вида:

А)

Б)

Таким образом сформулирована спектральная задача (5) по параметру а², описывающая распространение планарных волн в волноводе в виде полосы переменного сечения с производным знаком изменения толщины по координате х₂.

В реальных условиях разрушаемые во время бурения горные породы находятся в более сложном, чем при простых видах деформации, напряженном состоянии. Поэтому изучение механических свойств пород в условиях сложного всестороннего сжатия имеет большое практическое значение.

Исследование поведения горных пород в условиях всестороннего сжатия проводится с помощью приборов или установок, рассчитанных на высокие давления. Такие приборы состоят из цилиндра или «бомбы», внутри которых размещается исследуемый образец горной породы в виде или керна или прямоугольной призмы. Всестороннее давление на образец создается жидкостью, нагнетаемой в цилиндр или «бомбу».

При отсутствии тектонических движений на участке земной коры напряженное состояние горных пород осесимметрично относительно вертикали. Это позволяет охарактеризовать напряженное состояние горных пород двумя величинами в цилиндрической системе координат:

s_z = s_з и s_z = =s₁ = s₂

Вертикальные напряжения s_z зависят от веса вышележащих пород, поэтому можно записать:

s_z = — g_z,

где g — средняя плотность вышележащих пород;

z — глубина залегания пород.

В процессе сжатия вертикальным давлением горные породы в поперечном направлении деформируются не свободно. В этом случае имеет место равенство:

Отсюда получим:

Подставив значение s_z, получим формулу для упругого напряженного состояния горных пород:

В общем случае эта формула будет иметь вид:

Величина l называется коэффициентом бокового распора.

Задача о концентрации напряжений вокруг подземных горных выработок при воздействии сейсмических воли изучена недостаточно. Поскольку концентрации напряжений наблюдаются при статических внешних нагрузках, аналогичное явление должно иметь место и при динамических нагрузках. Задачи о концентрации напряжений может быть решены аналитическими, численными и экспериментальными методами. В настоящей работе рассматривается распространение гармонических воли в двумерном вязкоупругом теле с круглым отверстием при подходе волн с одной стороны. В такой постановке изучается наложение подходящих волн и отраженных от отверстия (а радиус отверстия) продольных и поперечных волн, что приводит к концентрации напряжений.

Основные уравнения теории вязко упругости для этой задачи о плоской деформации сводятся к следующим

где является потенциалами перемещения;

-плотность материала;

- дифференциальный оператор.

Рассмотрим падающую волну, порожденную линейным источником воли расширения, расположенным на расстоянии от полости.

Для описание вязко упругих свойств материала использовано ядро релаксации Ржаницына — Колтунова.

Исследованы значения динамического коэффициента концентрации напряжений для .

В случае значения динамической концентрации напряжений почти идентичны статическому случаю. Однако когда распределения напряжений довольно сильно отличаются от таковых для статического случая при соответствующих значениях. Если сравнить распределение напряжений для при с распределениями, полученными в работе, то очевидно, что распределение для ближе к распределению для плоской волны () при одном и том же волновом числе. Коэффициенты концентрации напряжений достигают максимальных значений на освещенной части полости. Установлено, что влияние вязко упругости окружающей среды заключается в увеличении реакции напряжения в цилиндре по сравнению с такой упруго не релаксирующей средой. Основная реакция напряжений в отверстие (неподкрепленное или подкрепленное) достигает на внутренней поверхности. А при воздействии аналогичным образом исследовано резонансные кривые, построенные для некоторых соотношений геометрических и физико-механических параметров системы, содержащих меньше резонансных пиков, чем упругих систем. Некоторые из этих пиков с формулированы не одной, а двумя эффект, объясняется взаимодействием колебаний собственных форм с близкими собственными частотами, возникающими вследствие наличия вязкого наследственного типа.