В последние годы не ослабевает интерес к исследованиям и разработке технологий основанных на использовании неоднородных тонкопленочных структур.
Пленочные покрытия способны повысить стойкость к окислению и диффузии, температуру плавления и микротвердость основного материала. Интерес к таким покрытиям также возрастает за счет развития исследований в области композиционных материалов. Многослойные пленочные структуры, состоящие из различных чередующихся слоев, зачастую обладают принципиально новыми механическими, оптическими, электрическими и магнитными свойствами, не характерными для однородных пленок. Пленочные покрытия получили широкое применение при решении многочисленных инженерных задач в электронной и оптоэлектронной промышленности. Технология производства таких устройств требует, чтобы наличие дефектов в них было сведено к минимуму.
Стоит отметить, что в такого рода инженерных конструкциях высокую важность представляют вопросы прочности соединения материалов с различными упругими свойствами. Основной причиной формирования дефектов в пленочных покрытиях является наличие рельефа поверхности пленки. Изменение формы поверхности может происходить на этапе выращивания и термической обработки пленочного покрытия, сопровождаемые процессами конденсации и испарения, и при других фазовых превращениях [10].
Исследование, проведенное в [3], показало, что образование рельефа поверхности пленки приводит к появлению дополнительных напряжений, которые отсутствуют в случае плоской поверхности. Анализ влияния искривленной поверхности пленки на напряженное состояние многослойной пленочной системы без учета поверхностного напряжения был представлен в работе [2].
Данная работа является продолжением исследований [3–9] по изучению механизма формирования регулярных структур на поверхности пленочного покрытия. Предполагается, что под действием интенсивного нагрева поверхность пленочного покрытия становится волнистой. Здесь рассматривается проблема потери устойчивости плоской формы поверхности пленочного покрытия при поверхностной диффузии. При этом в отличие от работы [2] учитывается поверхностное напряжение, которое позволяет учесть знак продольных усилий [1]. Задача формулируется в двумерной постановке.
Постановка задачи. В качестве модели многослойного пленочного покрытия толщины 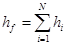 , осажденного на подложку толщины hs>>hf и находящегося в условиях плоской деформации, рассмотрим неоднородную упругую полуплоскость
, осажденного на подложку толщины hs>>hf и находящегося в условиях плоской деформации, рассмотрим неоднородную упругую полуплоскость 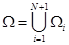 с прямолинейными межфазными границами
с прямолинейными межфазными границами 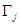 .
.
Пусть на границах отсутствуют скачки вектора напряжений и вектора перемещений. При решении задачи будем учитывать поверхностное напряжение [1,7,8]. Считаем, что равновесное состояние поверхности описывается обобщенным законом Лапласа-Юнга. В двумерном случае при отсутствии внешней нагрузки это условие было получено в работе [7].
В силу малости искривления будем считать, что с изменением рельефа поверхностное напряжение 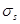 , также как и поверхностная энергия
, также как и поверхностная энергия 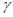 остаются постоянными.
остаются постоянными.
В подложке 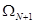 действует постоянное продольное напряжение
действует постоянное продольное напряжение 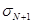 , при этом все остальные напряжения, а также угол поворота
, при этом все остальные напряжения, а также угол поворота 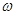 на бесконечности равны нулю. Морфологию поверхности пленки будем описывать посредством произвольной периодической функции
на бесконечности равны нулю. Морфологию поверхности пленки будем описывать посредством произвольной периодической функции
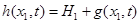 , (1)
, (1)
где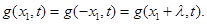
На коэффициенты разложения функции g(x1,t) в ряд Фурье накладываем следующие ограничения:
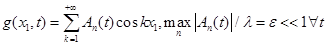 ,
,
здесь 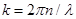 — волновое число.
— волновое число.
Значения параметров задачи, при которых 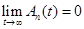 , будут соответствовать устойчивому состоянию плоской формы поверхности пленки. Требуется оценить влияние поверхностного напряжения на устойчивое состояние плоской формы пленочного покрытия.
, будут соответствовать устойчивому состоянию плоской формы поверхности пленки. Требуется оценить влияние поверхностного напряжения на устойчивое состояние плоской формы пленочного покрытия.
Эволюционное уравнение. Будем считать, что эволюция напряженной поверхности пленки происходит под действием поверхностной диффузии, определяемой производной химического потенциала вдоль поверхности. Считая, что диффузионный процесс локализован лишь в приповерхностном слое, запишем выражение для скорости движения точек поверхности [8]
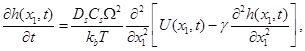 (2)
(2)
где Ω ̶ атомный объем, Ds ̶ коэффициент поверхностной самодиффузии, Cs ̶ концентрация поверхностных дефектов, kb ̶ постоянная Больцмана, T ̶ абсолютная температура.
Как и в [7, 8], процесс поверхностной потери устойчивости напряженного твердого тела рассматривается в квазистатической постановке. В силу чего для определения напряженно-деформированного состояния композита строится решение статической задачи теории упругости при фиксированном значении времени.
На основании комплексных потенциалов Гурса-Колосова, соотношений Мусхелишвили, принципа суперпозиции [4, 5] и метода возмущений решение сводится к системе интегральных уравнений Фредгольма второго рода. Поскольку форма свободной границы определяется выражением (1), решение задачи в каждом приближении находится в виде рядов Фурье.
Интегрирование уравнения (2) при условии 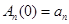 приводит к следующей зависимости амплитуды каждой гармоники возмущения от времени, физических и геометрических параметров задачи [9]
приводит к следующей зависимости амплитуды каждой гармоники возмущения от времени, физических и геометрических параметров задачи [9]
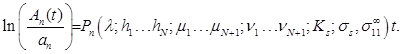
Численные результаты. Оценим влияние длины волны на морфологическую устойчивость поверхности двухслойного N=2 пленочного покрытия. При нахождении напряженно-деформированного состояния композита используем первое n=1 приближение в методе разложения по малому параметру. Критическому состоянию, при котором наблюдается потеря устойчивости плоской формы поверхности пленки, соответствует такое 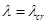 , при котором
, при котором 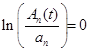 . При
. При 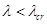 происходит сглаживание рельефа.
происходит сглаживание рельефа.
В качестве параметров задачи используем следующие константы: h1=0,08 мкм и 0,16 мкм, h2=0,08 мкм и 0,16 мкм, ν1=ν2=ν3=0,3, σ0=±1 ГПа, σs = γ =1 Н/м, μ1=100 ГПа, 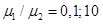 и
и 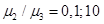 .
.
Учет поверхностного напряжения позволяет оценить влияние знака продольных усилий [1]. В таблице 1 приведены относительные разности критических значений длин волн 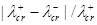 , при разных знаках продольных усилий для пленок различной толщины.
, при разных знаках продольных усилий для пленок различной толщины.
Таблица 1
Влияние знака продольных усилий
|
μ1/μ2 |
10 |
10 |
1/10 |
1/10 | |
|
μ2/μ3 |
10 |
1/10 |
10 |
1/10 | |
|
h1 |
h2 |
| |||
|
0.08 |
0.08 |
0.00463 |
0.007062 |
- |
- |
|
0.08 |
0.16 |
0.004594 |
0.0059 |
- |
- |
|
0.16 |
0.08 |
0.006983 |
0.009162 |
0.05709 |
- |
Как видно из Таблицы 1, влияние знака продольных усилий оказалось незначительным, за исключением случая, когда пленочная система описывается следующими параметрами: h1=0,16 мкм, h2=0,08 мкм, 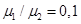 ,
, 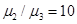 — здесь относительная разность критических значений длин волн при различных знаках продольных усилий составила порядка 6 %.
— здесь относительная разность критических значений длин волн при различных знаках продольных усилий составила порядка 6 %.
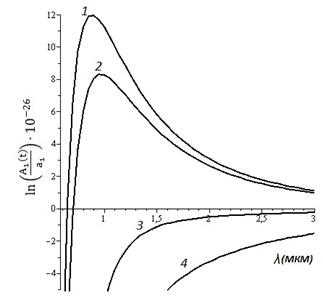
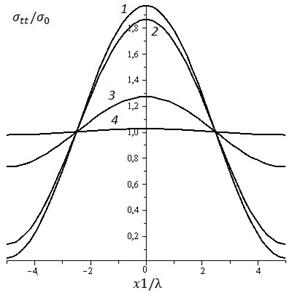
а) б)
Рис. 1. Относительная амплитуда (а) и напряжения (б)
На Рис.1. представлены графики относительной амплитуды и напряжений для двухслойного пленочного покрытия, при h1=0,08 мкм, h2=0,08 мкм, ν1= ν2= ν3=0,3,
σ0=±1 ГПа, γ =1 Н/м, μ1=100 ГПа без учета поверхностного напряжения σs = 0 Н/м. Кривые 1–4 соответствуют следующим отношениям жесткостей материалов: 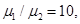
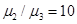 ;
; 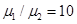 ,
, 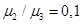 ;
; 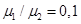 ,
, 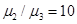 и
и 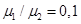 ,
, 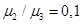 .
.
Литература:
1. Grilhe J. Study of roughness formation induced by homogeneous stress at the free surfaces of solids // Acta Metallurgica and Materialia, 1993. Vol. 41, N 3. P. 909–913.
2. Kim J.-H., Vlassak J. J. Perturbation analysis of an undulating free surface in a multi-layered structure // Int. J. Solids and Structures. 44 (2007) 7924–7937.
3. Викулина Ю. И., Греков М. А., Костырко С. А. Модель пленочного покрытия со слабо искривленной поверхностью // Изв. РАН. Механика твердого тела. 2010. № 6. С. 16–28.
4. Греков М. А., Костырко С. А. Многослойное пленочное покрытие под действием периодической системы поверхностных сосредоточенных сил // Труды ЦНИИ им. акад. А. Н. Крылова. 2010. Т. 53. C. 29–36.
5. Греков М. А., Костырко С. А. Напряженное состояние тонкого покрытия при действии периодической системы поверхностных сосредоточенных сил // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. 2004. № 3–4. С. 99–107.
6. Греков М. А., Костырко С. А. Пленочное покрытие на шероховатой поверхности упругого тела // Прикладная математика и механика. 2013. Т. 77. Вып. 1. С.113–128.
7. Греков М. А., Костырко С. А. Потеря устойчивости плоской формы пленочного покрытия при поверхностной диффузии // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. 2007. № 1. С. 46–54.
8. Костырко С. А. Влияние формы возмущения на устойчивость плоской поверхности пленочного покрытия при диффузионных процессах // Вестник Санкт-Петербургского университета. Серия 10: Математика. Механика. Астрономия. 2011. № 3. С. 101–111.
9. Костырко С. А., Шувалов Г. М. Образование дефектов поверхности многослойного пленочного покрытия при диффузионных процессах // Процессы управления и устойчивость. 2014. Т. 1. № 1. С. 169–174.
10. Пронина Ю. Г. Оценка устойчивости упругой трубы под давлением коррозионных сред // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. 2006. № 3. С.55–63.

