Ключевые слова:ультразвук, дифракционная гипербола, трассировка лучами, дифракция лучей.
Цель работы. Разработать последовательный алгоритм построения ультразвуковой дифракционной картины для двумерной области, пригодный для программной реализации на языке высокого уровня.
Введение. В настоящее время задача ультразвукового моделирования достаточно широко представлена: в медицине, эхолотировании, сейсморазведке. В этих областях решается задача определения внутренних свойств структур при отсутствии непосредственного доступа к этим структурам. Например, диагностика сварных швов нефтепроводов, определение залежей ценных ископаемых или анализ состояния щитовидной железы пациента. При этом используются ультразвуковые методы визуализации, которые имеют некоторые недостатки в связи со сложностью эффектов, возникающих при распространении ультразвуковых волн, и поэтому представляют интерес для моделирования. Одним из таких методов получения ультразвуковой картины является метод лучевой трассировки, когда источником производится пуск ультразвуковых волн, распространение которых рассматривается согласно законам геометрической оптики [1]. В статье рассмотрен алгоритм реализации данного метода для моделируемой области при использовании совмещенного источника/приемника волн.
Этапы работы. Рассмотрим область S, содержащую некоторые объекты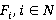 
, представляющие собой набор кусочно-линейных функций (сегментов) 
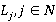, и представляющих границы разнородных сред внутри моделируемой области, причем для каждого объекта 
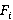определены некоторые свойства, например, волновое сопротивление, а также скорости прохождения ультразвуковых лучей сквозь эти объекты по формуле Урупова-Дикса, позволяющей оценить скорость любого горизонтального слоя без предварительного вычисления скоростей предшествующих слоев [2]:
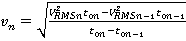(1)
Где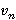 
— интервальная скорость в пределах слоя, ограниченного n — 1 границей сверху и n-ой границей снизу, 
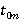и 
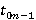- соответствующие времена для нормального падения, 
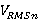, и 
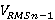— соответствующие среднеквадратические скорости
На первом этапе производятся предварительные вычисления: определение дифракционного угла (угла, ограничивающего дифракционную гиперболу), представление гладких кривых в линейно-кусочном виде, а также нахождение и инициализация точек дифракции.
Модель с набором объектов необходимо представить в осях (x, z), где x представляет собой ось, вдоль которой движется источник ультразвуковых волн, а z — ось, вдоль которой производится пуск волн. Тогда матрица отражений на осях (x, z) представляет собой следующую структуру в виде матрицы:
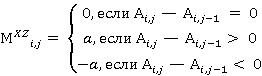, (2)
Где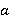 
— некоторое неотрицательное число, характеризующее разницу коэффициентов отражения сред, Ai,j –параметр коэффициента отражения объекта в точке (i, j) области S.
Следующий шаг — это отображение полученной в осях (x, z) матрицы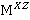 
на временную ось, то есть перестроение модели в осях (x, t). Для осуществления отображения необходимо для каждой точки области S определить время прохождения ультразвуковым сигналом расстояния от источника до данной точки. Причем, следует разделять точки пространства на обычные, для которых без изменений применимы законы геометрической оптики, и особые точки, являющиеся точками дифракции, для которых стоит внести определенные правки. Каждая точка дифракции является в некоторой степени уникальной, поскольку учитывается ее расположение относительно границ объектов модели.
Рассмотрим точки A и B (рис. 1):
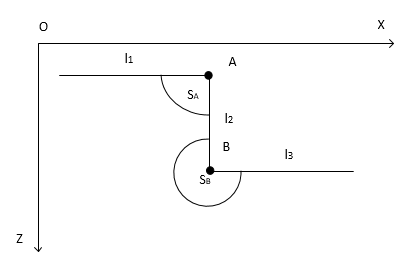
Риc. 1. Особые точки модели
Где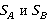 
это теневые области точек дифракции. Теневые области означают, что в этих секторах прямые лучи от источника не могут быть получены точкой дифракции. Это, в свою очередь, означает, что точкой B для сектора 
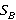, заключенного в диапазоне 
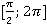, будут получены только преломленные на границе 
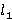лучи R(i, ɑ0) и R(i, ɑ1) (рис. 2):
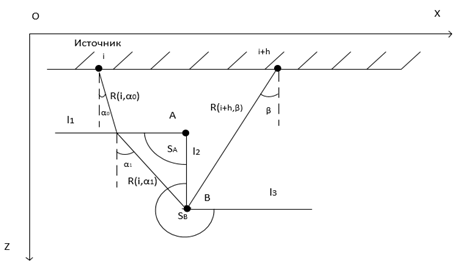
Рис. 2. Преломление на границе
Итак, для построения матрицы в осях (x, t), составим следующий алгоритм:
1) Определить точки дифракции, а также связанные с ними границы. То есть для каждой фигуры 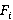области S определить структуру данных с информацией о точках дифракции 
, 
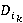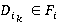
2) В пределах угла дифракции производить пуск лучей, представляющих звуковые волны, и рассчитываемых по законам геометрической оптики.
3) На границе разделов сред рассчитывать преломленные и отраженные лучи. Причем отражения происходят зеркально углу падения, а преломления рассчитываются в зависимости от волновых сопротивлений сред.
4) Для каждого из отраженных и преломленных лучей рекурсивно повторяются шаги 2–3 до достижения необходимой глубины моделирования.
5) Вычисление в осях (x, t) дифракционных гипербол производится по следующей формуле:
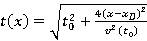(3)
Где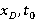 
— координаты вершин гипербол, 
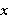— текущие координаты гипербол, а 
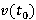— задаваемый скоростной закон.
Построение подобной лучевой картины позволяет эффективно рассматривать моделируемую область, но требует достаточно большого расхода памяти и существенного времени построения. Произведем вычислительную оценку алгоритма. Из каждой точки из множества M точек отсчета по оси x производится пуск лучей в пределах угла A с последующим рекурсивным (глубины N) вычислением отраженных и преломленных лучей. Для параметров M, A и N получаем следующую оценку сложности: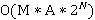 
. Несмотря на то, что алгоритм оказывается вычислительно весьма требователен, полученная в результате структура удобна тем, что позволяет делать «срез» моделируемой области в разных точках и на разных этапах построения, а использование различных средств языков программирования (напр. отложенные или ленивые вычисления (англ. lazy evaluation), позволяющие производить вычисления только при непосредственном доступе к результатам вычислений [3]) позволит оптимизировать доступ к данным.
Луч удобно представлять набором уникальных параметров, представляющих собой некоторые полезные для вычислений данные, как то: углы пуска, углы отражений, точки пересечений, точки пуска, импульс и т. д.
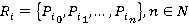(4)
Для каждого луча в процессе построения рассматривается две ситуации: выход за пределы моделируемой области и пересечение некоторой внутренней границы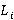 
области S. Если точка пересечения луча и границы объекта обладает свойствами дифракции, то в этом случае необходимо учитывать изменение свойств распространения лучей, а именно: дифрагированные волны, как правило, имеют меньшие амплитуды по сравнению с амплитудами отраженных волн [4, 5]. Рассмотрим рис. 3. Для луча R отраженные от точки дифракции лучи будут выглядеть следующим образом.
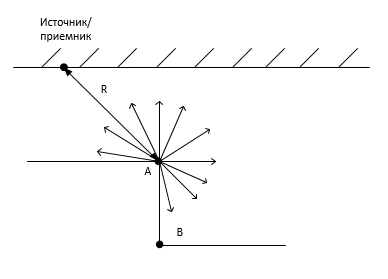
Рис. 3 Отраженные лучи в точке дифракции
Так как рассматривается случай совмещенного источника/приемника, то приемником в точке пуска будет получен отраженный от точки дифракции единственный луч, направленный в противоположную пуску сторону. Таким образом, вдоль оси x в пределах дифракционного угла будем получать сигналы, отраженные от точек дифракции, получая на временной модели (x, t) дифракционные гиперболы [6].
Для точек, не являющихся точками дифракции, отраженные лучи будут возвращаться к источнику только в двух случаях: падая перпендикулярно на ближайшие границы, либо в случае переотражений, в результате которых конечная точка луча должна совпасть с начальной точкой пуска луча. (рис. 4)
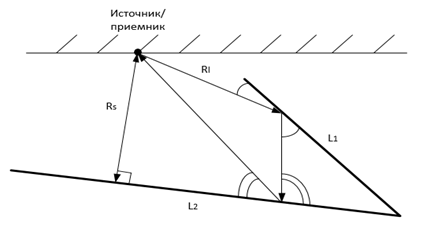
Рис. 4. Ситуация возвращения двух лучей к источнику
При этом может возникнуть ситуация, когда многократно переотраженные лучи достигают приемника быстрее луча, идущего к границе перпендикулярно и имеющего минимальный путь. Происходит это из-за наличия неоднородностей в среде. А для наклонных границ наблюдается эффект миграции (смещение представления границ на временной оси относительно их первоначального расположения). Это означает необходимость хранить в луче историю его состояний.
Итак, для построения модели в осях (x, t) дополнительно необходимо выполнить следующие два шага:
1) Для каждого луча, полученного приемником, рассчитать время его пути, которое будет рассчитываться как сумма времен прохождения линейных участков луча. Сформировать трассы, представляющие собой значение импульса и время, на котором он был зафиксирован приемником. Набор трасс формирует двумерный массив, представляющий собой матрицу отражений границ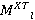 
.
2) Для каждой точки дифракции необходимо аналогично п.1 получить матрицы отражений точек дифракции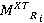 
3) Произвести суммирование матриц:
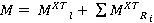(5)
Результирующая матрица будет содержать информацию о всех неоднородностях среды. В результате сложения матриц можно будет наблюдать эффект интерференции волн на участках, где для разных границ лучи, пущенные в разных направлениях, придут в одну точку с одним и тем же временем (неоднозначность времен прихода лучей).
Заключение. В результате работы был составлен достаточно подробный алгоритм моделирования ультразвуковой дифракционной картины, заключающийся в построении матрицы отражений для моделируемой области, последовательной трассировке области, а также построения матриц отражений поверхностей и точек дифракции на временной оси для получения итоговой ультразвуковой дифракционной модели. Несмотря на вычислительную сложность, алгоритм предоставляет гибкий инструмент для анализа. Были описаны структуры данных и произведена оценка сложности алгоритма, а сам алгоритм подготовлен для реализации на произвольном языке программирования.
Литература:
1. Ковригин С. Д. Архитектурно-строительная акустика: Учеб. пособие для вузов, — М.: Высшая школа, 1980, — 184 с.
2. Воскресенский Ю. Н. Построение сейсмических изображений. Учеб. пособие для вузов, — М.: РГУ нефти и газа, 2006, 116 с.
3. Мартин Фаулер, Архитектура корпоративных программных приложений, Вильямс, 2008, 544 с.
4. Никитченко, А. Н. Исследование дифрагированных сейсмических волн и их применение для построения изображения среды, автореф. дис. на соиск. учен. степ. канд. ф-м. наук (25.00.10) / Никитченко, Андрей Николаевич; Санкт-Петербург, 2011. — 89 с.
5. Pat F. Daley, Numerical experiments in high frequency diffraction theory, CREWES Research Report Volume 20, 2008
6. V. Khaidukov, Diffraction imaging by focusing-defocusing: An outlook on seismic superresolution/ V. Khaidukov, E. Landa, and T. J. Moser — GEOPHYSICS, VOL. 69, NO. 6, 2004; P. 1478–1490
