Разработана математическая модель анализа прямых и отраженных от различных объектов электромагнитных волн на примере плавучего ледового массива. В основе модели лежат направленные функции Грина с неоднородными по углу граничными условиями. Данная модель позволяет решать задачи анализа антенн.
Ключевые слова: функция Грина, дистанционное обнаружение объектов, электромагнитные волны.
Передача информации по морю и суше в большинстве случаев осуществляется с помощью электромагнитных волн, т. к. электромагнитные волны являются одними из наиболее быстрых переносчиков энергии и информации, поэтому анализ электромагнитных полей является важной задачей в радиолокации и радиосвязи.
В статье представлена математическая модель, построенная на «направленных функциях Грина» с зависимостью от угла.
Модель позволяет определить распределение напряженности электрического поля точечного источника электромагнитных волн вблизи массива льда.
Приведены результаты расчетов, показавшие применимость выведенной математической модели для практических расчетов. Погрешность расчетной модели не превышает 25 %.
Математическая модель
Рассмотрим следующую задачу: нужно рассчитать поле точечного источника электромагнитных волн, расположенного в воздухе вблизи массива льда (Рис. 1). Известны следующие характеристики: магнитная и диэлектрическая проницаемости воздуха и массива льда.
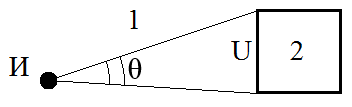
Рис. 1. Геометрия рассматриваемой задачи. И — источник, U — поверхность объекта, θ — угол между. 1-воздух, 2-массив льда
Решение задачи можно представить в виде двух сопряженных функций Грина. Одна из функций Грина описывает расходящиеся от поверхности излучателя волны G l (M,M 0 ), а сопряженная с ней функция G l -1 (M,M 0 ) — отраженные [1, 3]. Сумма этих двух функций и будет решением уравнения Гельмгольца [1, 5]:
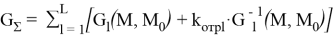
M — точка приема сигнала с координатами x и y;
M0 — точка излучения сигнала с координатами x0 и y0;
Направленная функция Грина имеет вид:
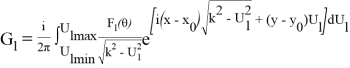
где F l (θ) =1, если θ lmin ≤ θ ≤ θ lmax при l=1,2,3,…,l. F l =0 при остальных значениях θ.
В данной работе сферические волны представлены в виде суперпозиции плоских волн [2], поэтому справедливо использование коэффициента отражения для плоских волн [2, 4]:
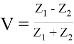
Z l — волновое сопротивление l — й среды, равное:
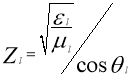
Направленна функция Грина для отраженной волн запишутся как:
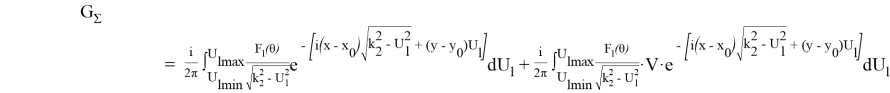
Выражение (5) описывает распределение напряженности падающих и отраженных волн в пространстве вблизи ледового массива.
Результаты численных расчетов
На рисунках 2–4 приведены результаты расчетов по предложенной теории при расположении источника в слое льда.
Пик напряженности на графиках 2–4 «показывает» местоположение объекта.
Исходные данные: частота излучателя f=10 МГц; расчетное расстояние составляет 2000 м, мощность излучателя P = 4000 Вт
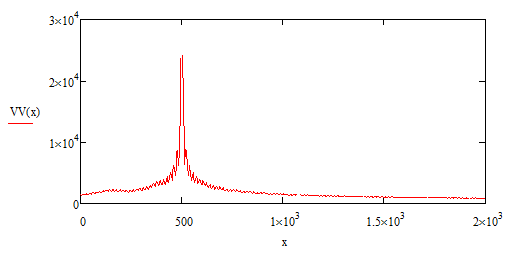
Рис. 2. График распределения напряженности электрического поля в свободном пространстве, координаты источника сигнала x=500 м, y=0 м
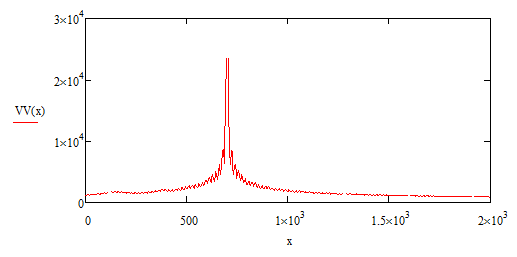
Рис. 3. График распределения напряженности электрического поля в свободном пространстве, координаты источника сигнала x=700 м, y=0 м
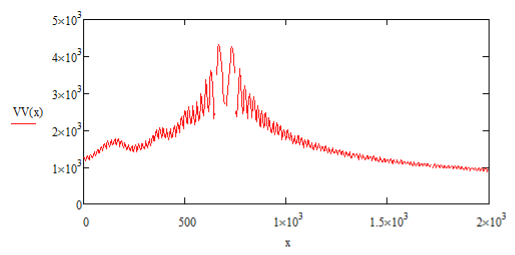
Рис. 4. График распределения напряженности электрического поля в свободном пространстве, координаты источника сигнала x=700 м, y=100 м
Погрешность расчетов
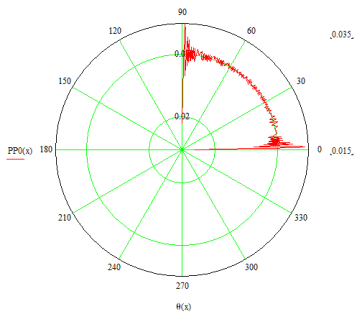
Рис. 5. Диаграмма направленности точечного излучателя по формулам (1) и (3)
Наибольшие отклонения вблизи углов 0º и 90º обуславливаются ошибками разработанного алгоритма. В интервале от 5º до 85º погрешность не превышает 5 %.
Выводы
Данные теоретических исследований распространения электромагнитных волн можно использовать для:
а) обнаружения электродинамических аномалий в воздухе, источником которых могут являться различные атмосферные явления, вызывающие местные изменения диэлектрической проницаемости.
б) для навигации судов в стеснённых условиях, обнаружения кромок ледовых полей, мониторинга океанской поверхности и т.д;
д) исследовании физических свойств различных веществ;
е) дальности распространения электромагнитных волн в заданных условиях.
Литература:
- Короченцев В. И. Волновые задачи теории направленных и фокусирующих антенн. Владивосток: Дальнаука, 1998. 192 c.
- Бреховских Л. М. Волны в слоистых средах. М.: Наука, 1973. 340 с.
- Шевкун С. А. Разработка методов анализа волновых полей в замкнутых объемах: дис., канд. физ.-мат. наук. Владивосток, 2006. 186 с.
- Шендеров Е. Л. Волновые задачи гидроакустики. Ленинград: Судостроение, 1972. 348 с.
- Korochentsev V. I., Zorchenko N. K., Potapenko A. A. Methods for reducing the error of sonar equipment in sea wedge. Materials 2017 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM 2017), Chelyabinsk, 2017, pp. 1432–1435.
- https://cyberleninka.ru/article/n/matematicheskaya-model-rasprostraneniya-sfericheskih-elektromagnitnyh-voln-v-sloe-lda

