Разработана математическая модель распространения сферических электромагнитных волн внутри слоя льда. В основе модели лежат направленные функции Грина с неоднородными по углу граничными условиями. Такая модель позволяет представить неоднородную поверхность как совокупность однородных поверхностей, что позволяет использовать простые и широко распространенные методы анализа волновых полей.
С помощью предложенной модели проведен анализ поля точечного направленного источника сферических электромагнитных волн, расположенных внутри слоя льда. Также приведены результаты расчетов при разных частотах и разной толщине слоя льда. Максимальная погрешность алгоритма составляет от 20 до 25 %.
Ключевые слова: анализ волновых полей; граница раздела сред; направленная функция Грина.
Математическая модель
Рассмотрим следующую задачу: нужно рассчитать поле точечного источника, помещенного в лед на небольшом расстоянии от границы раздела «лед-атмосфера». Излучение проводится на границу раздела «лед-атмосфера» (Рис. 1). Известны следующие характеристики: магнитная и диэлектрическая проницаемости воздуха, моря, льда, частота и мощность источников излучения.
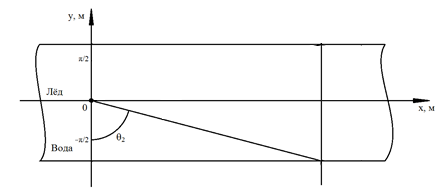
Рис. 1. Геометрия рассматриваемой задачи: И — источник излучения, 1 — лед, 2 — водное полупространство
Как известно, равноправными решениями уравнения Гельмгольца являются две сопряженные друг с другом функции Грина. Одна из функций Грина описывает расходящиеся от поверхности излучателя волны Gl (M,M0), а вторая — сопряженная с ней Gl-1 (M,M0) [1, 3]. Строго говоря, общим решением уравнения Гельмгольца необходимо считать сумму этих функций:
![]() (1)
(1)
M — точка приема сигнала с координатами x и y;
M0 — точка излучения сигнала с координатами x0 и y0;
Направленная функция Грина имеет вид:
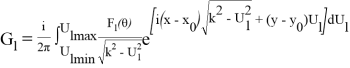 (2)
(2)
где Fl(θ) =1, если θlmin ≤ θ ≤ θlmax при l=1,2,3,…,l. Fl =0 при остальных значениях θ.
В данной работе сферические волны представлены в виде суперпозиции плоских волн, поэтому справедливо использование коэффициента отражения для плоских волн:
![]() (3)
(3)
Zl — волновое сопротивление l — й среды, равное:
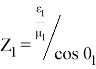 (4)
(4)
Согласно поставленной задаче функция Грина для прошедшей волны запишется:
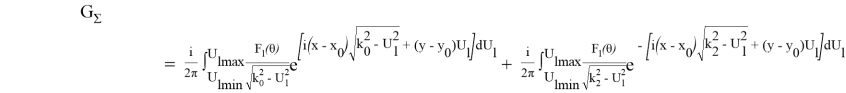 (5)
(5)
Выражение (5) описывает амплитудное распределение точечного источника в слое льда.
Результаты расчетов
Моделирование проведено в программной среде MathCad. В ходе моделирования изменялись только частота излучателя и толщина слоя льда. Приведено три графика.
Исходные данные расчета поля точечного излучателя представлены в таблице 1, в которой указаны параметры:
c — фазовая скорость распространения электромагнитных волн в среде;
f — частота излучателя;
P — мощность излучателя;
ε — диэлектрическая проницаемость среды;
μ — магнитная проницаемость среды.
В графиках показана зависимость амплитуды компоненты электрического поля PP2(x) от расстояния x.
Таблица 1
Исходные данные
Физические характеристики сред
|
№рисунка |
№среды |
f, МГц |
P, МВт |
c, м/с |
ε |
μ |
|
2 |
1 |
1 |
4 |
2,29·108 |
87 |
1 |
|
2 |
1,8·108 |
3,25 |
1 | |||
|
3 |
1 |
10 |
4 |
2,29·108 |
87 |
1 |
|
2 |
1,8·108 |
3,25 |
1 | |||
|
4 |
1 |
100 |
4 |
2,29·108 |
87 |
1 |
|
2 |
1,8·108 |
3,25 |
1 |
Графики:
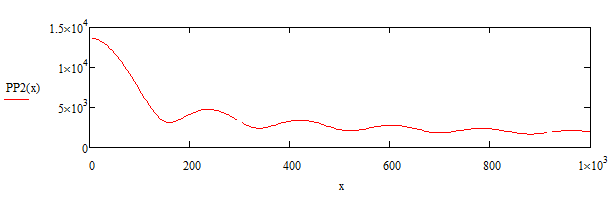
Рис. 2. График распределения амплитуды электрической составляющей падающей и отраженной волн в пространстве
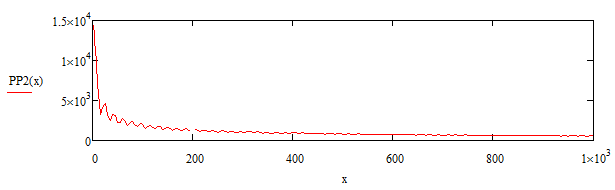
Рис. 3. График распределения амплитуды электрической составляющей падающей и отраженной волн в пространстве
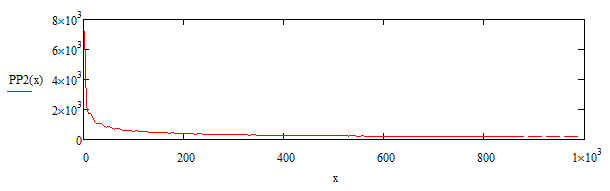
Рис. 4. График распределения амплитуды электрической составляющей падающей и отраженной волн в пространстве
Главным преимуществом метода является скорость вычисления (2–3 минуты при расчете значений функции Грина в 1000 точек на ноутбуке средней мощности).
Приведенная математическая модель может быть применена в задачах, где предполагается, что в однородной среде присутствуют области с параметрами отличными от внешней среды, при этом на границе раздела параметры сред меняются скачкообразно.
Выводы
Полученные данные можно использовать для исследования физических свойств Арктических льдов, дальности распространения электромагнитных волн в слоях льда.
Литература:
- Бреховских Л. М. Волны в слоистых средах. — М.: Наука, 1973. 340 с.
- Шендеров Е. Л. Волновые задачи гидроакустики. — Ленинград: Судостроение, 1972. 348 с.
- Лобова Т. Ж., Короченцев В. И. Модель антенной решетки в замкнутом объеме. — Владивосток: Вестник инженерной школы ДВФУ, 2018. 5с.
- Короченцев В. И. Волновые задачи теории направленных и фокусирующих антенн. — Владивосток: Дальнаука, 1998. 192 c.
- Шевкун С. А. Разработка методов анализа волновых полей в замкнутых объемах: диссертация. … канд. физ.-мат. наук. — Владивосток, 2006. 186 с.
- Корчака А. В. Математическая модель излучателя сферических волн в слоистой среде — Владивосток: Вестник инженерной школы ДВФУ, 2018. 5с.

