Разработана математическая модель синтеза антенных решеток из пяти точечных излучателей. В основе модели лежат направленные функции Грина, удовлетворяющие граничным условиям неразрывности по угловым координатам. С помощью предложенной модели проведен синтез пятиэлементной антенной решетки электромагнитных волн точечного направленного источника сферических электромагнитных волн, находящихся в свободном пространстве. Также приведены результаты расчетов при разных частотах. Максимальная погрешность алгоритма составляет от 20 до 25 %.

Ключевые слова: синтез антенн, граница раздела сред, направленная функция Грина.

Математическая модель

Рассмотрим следующую задачу: нужно определить взаимное расположение источников, если известно пространственное распределение амплитуды электрического поля. Известны следующие характеристики: магнитная и диэлектрическая проницаемости воздуха, мощность источников излучения.

Рис. 1. Геометрия рассматриваемой задачи. И — источник излучения, П — приемник, λ — длина волны

Достаточно большое количество математических моделей, описывающих распространение электромагнитных волн, строятся на частных решениях волнового уравнения и уравнений Максвелла с граничными условиями неразрывности амплитуды поля и неразрывности волнового сопротивления [1,3]. Решением волнового уравнения является уравнение Гельмгольца, а равноправными решениями уравнения Гельмгольца являются две сопряженные друг с другом функции Грина [2, 4]. Одна из функций Грина описывает расходящиеся от поверхности излучателя волны G _l (M,M ₀ ), а вторая — сопряженная с ней G _l ^-1 (M,M ₀ ) [5]. Строго говоря, общим решением уравнения Гельмгольца необходимо считать сумму этих функций:

(1)

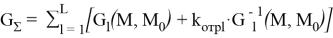
M — точка приема сигнала с координатами x и y;

M0 — точка излучения сигнала с координатами x ₀ и y ₀ ;

Направленная функция Грина имеет вид:

(2)

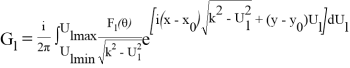
где F _l (θ) =1, если θ _lmin ≤ θ ≤ θ _lmax при l=1,2,3,…,l. F _l =0 при остальных значениях θ.

Результаты расчетов

Моделирование проведено в программной среде MathCad. В ходе моделирования изменялись только частота излучателя и толщина слоя льда. Приведено три графика.

Исходные данные расчета поля точечного излучателя:

c — фазовая скорость распространения электромагнитных волн в среде 3·10 ⁸ м/с;

f — частота излучателя;

P — мощность излучателя;

В графиках показаны зависимости амплитуды компоненты электрического поля PPS(x) и функции плотности источников VVS(x) от расстояния x.

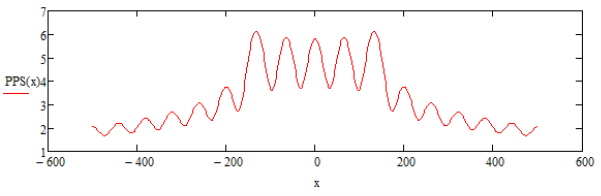
Рис. 2. График распределения амплитуды напряженности электрического поля в пространстве. f = 5 МГц, P = 35Вт

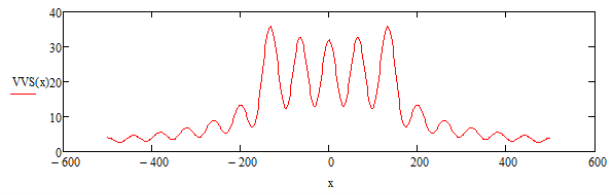
Рис. 3. График распределения функции плотности источников. f = 5 МГц, P = 35Вт

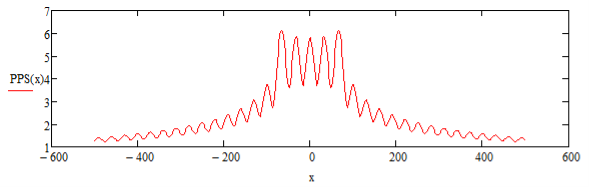
Рис. 4. График распределения амплитуды напряженности электрического поля в пространстве. f = 10 МГц, P = 35Вт

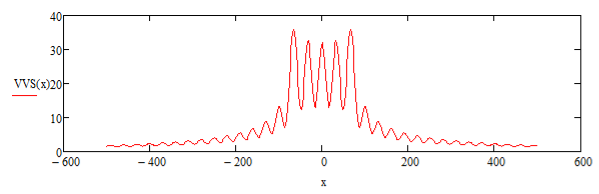
Рис. 5. График распределения функции плотности источников. f = 10 МГц, P = 35Вт

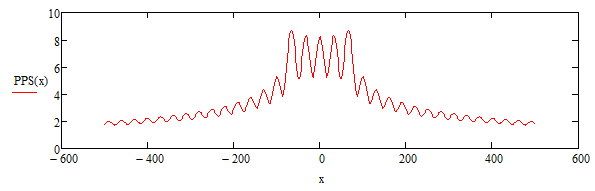
Рис. 6. График распределения амплитуды напряженности электрического поля в пространстве. f = 10 МГц, P = 70 Вт

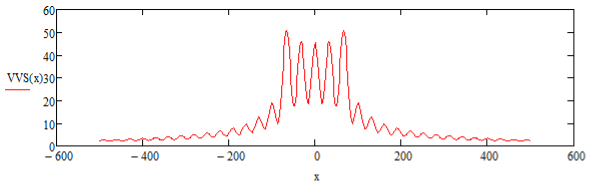
Рис. 7. График распределения функции плотности источников. f = 10 МГц, P = 70 Вт

Выводы

Главным преимуществом метода является скорость вычисления (2–3 минуты при расчете значений функции Грина в 1000 точек на ноутбуке средней мощности).

Приведенная математическая модель может быть применена для моделирования распространения электромагнитных волн от нескольких источников в свободном пространстве.

Литература:

1. Фок В. А. Проблемы дифракции и распространения электромагнитных волн. ˗ М.: Советское радио, 1970. 476 с.
2. Шендеров Е. Л. Волновые задачи гидроакустики. — Ленинград: Судостроение, 1972. 348 с.
3. Бреховских Л. М. Волны в слоистых средах. — М.: Наука, 1973. 340 с.
4. Cross J. D., Atkins P. R., Electromagnetic Propagation in Four-Layered Media Due to a Vertical Electric Dipole: A Clarification. Institute of Electrical and Electronics Engineers, 2015 vol. 2, issue: 2. Available at: https://ieeexplore.ieee.org/document/6991576
5. Короченцев В. И. Волновые задачи теории направленных и фокусирующих антенн. — Владивосток: Дальнаука, 1998. 192 c.