В данной статье описывается метод экспериментального наблюдения интерференции. При разделении волнового фронта пучка света зеркалами Френеля и бипризмой Френеля возникает явление интерференции. Определяется длина волны по картине интерференционных полос.
Ключевые слова: длина волны, фаза, бипризма Френеля, зеркало Френеля, мнимый источник света.
This article describes a method for experimental observation of interference. When the wavefront of a light beam is separated by Fresnel mirrors and a Fresnel biprism, the phenomenon of interference occurs. The wavelength is determined by the pattern of interference fringes.
Keywords : wavelength, phase, Fresnel biprism, Fresnel mirror, imaginary light source.
В данной статье мы будем решать следующие задачи:
Определить длину волны света при помощи интерференции
1. При помощи зеркала Френеля
2. При помощи бипризмы Френеля
Таблица 1
Оборудование
|
Бипризма Френеля |
08556.00 |
1 |
|
Подставка для призмы с креплением |
08254.00 |
1 |
|
Зеркало Френеля |
08560.00 |
1 |
|
Линзы, вставляемые, f = +20 мм |
08018.01 |
1 |
|
Линзы, вставляемые, f = +300 мм, бесцветный |
08025.01 |
1 |
|
Держатель для линз |
08012.00 |
2 |
|
Поворотный кронштейн |
08256.00 |
1 |
|
Ползунок с креплением для опт. скам. h = 30 мм |
08286.01 |
2 |
|
Ползунок с креплением для опт. скам. h = 80 мм |
08286.02 |
2 |
|
Оптическая скамья l = 1000 мм |
08282.00 |
1 |
|
Подставка для опт. скам., регулируемая |
08284.00 |
2 |
|
Лазер, He-Ne 1.0 мВт. 220 В перем. ток |
08181.93 |
1 |
|
Рулетка, h = 2 м |
09936.00 |
1 |
Подготовка и измерения
Экспериментальная установка для получения интерференции при помощи зеркал Френеля показана на Рис. 1. На оптической скамье закрепляются лазер (2см), держатель для линз и линзы с фокусным расстоянием f = 20 мм (23,3 см) и установка с зеркалом Френеля (43,2 см). Освещенная поверхность на расстоянии примерно от 2 до 5 м используется в качестве экрана.
Перед началом эксперимента подвижная часть зеркал Френеля устанавливается таким образом, чтобы 2 половинки зеркала были практически параллельны.
Поверхность зеркала располагается параллельно оптической скамье. Лазер устанавливается таким образом, чтобы расширенный пучок луча равномерно попадал на обе половинки зеркала.
В результате на экране отображаются два световых пятна разделенных затемненной областью. Поворачивая регулировочные винты зеркал Френеля, подвижная часть зеркала поворачивается до тех пора, пока эти зоны не перекроются. Наблюдаемая интерференционная картина и ее зависимость от угла наклона зеркал наблюдается на экране. Интерференционная картина должна иметь вид, аналогично показанной на Рис. 4.
Экспериментальная установка с бипризмой аналогична установке, показанной на Рис. 1 (справа). На оптической скамье помимо лазера и первой линзы установлены ползунок с креплением для призмы и бипризма (45 см), а так же держатель для линзы и линза с фокусным расстоянием 300 мм (примерно 60 см).
(Нельзя смотреть непосредственно на неослабленный лазерный луч.

Рис. 1. Экспериментальная установка для получения интерференции при помощи зеркал Френеля
Расширенный луч попадает на центральное ребро бипризмы. При помощи линзы, расположенной на расстоянии 60 см, два мнимых источника света проецируются на освещенную поверхность, находящуюся на расстоянии примерно 3 м. Измеряется расстояние между двумя точечными источниками, изображающей линзой и изображением и расстоянием до объекта — расстояние между линзой 1 и линзой 2 минус фокусное расстояние линзы 1. Если устраняется линза 2, то наблюдается интерференционная картина. Измеряется расстояние т последующих интерференционных полос.
Теория и вычисления
Если свет длиной волны λ из двух точечных источников, чья разность фаз постоянна (когерентность), падает в точку Р, то два луча света интерферируются. Если две амплитуды вектора распространения в направлении по оси х имеют вид:
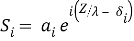
где,
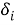
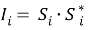
то в результате совмещения получаем
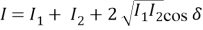
где
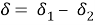
В соответствии с уравнением (1) I имеет максимум и минимум, как функция от разности фаз δ. В случае зеркал Френеля волна от источника света Q падает на два зеркала, наклоненных : под углом α. Интерференционная картина наблюдается на экране S. Зеркало с источником света можно заменить двумя источниками когерентного света Q 1 и Q 2 расположенными на расстоянии d друг от друга.
Если r это расстояние между Q и точкой соприкосновения зеркал А, то из Рис.2 получаем:
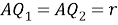
и

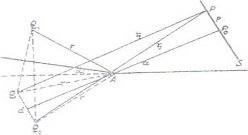
Рис. 2. Геометрическое расположение при использовании зеркал Френеля
Если расстояние α между экраном и зеркалами велико по сравнению с расстоянием между двумя соседними интерференционными максимумами, то при определенном приближении имеет место, следующее равенство:
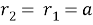
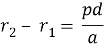
т. к.
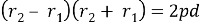
Разность фаз δ таким образом
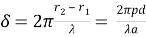
В соответствие с уравнением (1) максимум, возникающий на экране для расстояний p , равен:
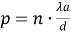
и минимум
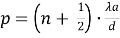
Расстояние d между двумя мнимыми источниками света определяются путем проекции их четкого изображения на экран, используя линзу с фокусным расстоянием f и измеряя размер изображения В
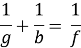
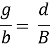
где g и b — расстояние от объекта до линзы и от изображения до линзы соответственно.
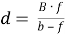
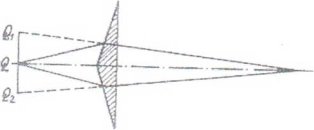
Рис. 3. Геометрическое расположение при использовании бипризмы Френеля

Рис. 4. Интерферограмма зеркал Френеля
Из этого, а также из уравнения (2) и (3), λ определяется, как среднее нескольких измерений используя различные углы наклона зеркал.
n = 1 и формула (2)
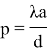
или
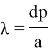
при
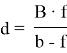
α — расстояние между двумя соседними максимумами
λ = 626,5 нМ.
В случае бипризмы Френеля расстояние d определяется точно также как и в случае зеркал Френеля, используя уравнение (4).
Уравнение (3) аналогичным образом используется для расстояния р между интерференционными полосами, если влияние показателя преломления и толщина призмы не принимается во внимание. Используя уравнения (4), (3) и (2) значения λ определяется как λ = 624,0 нМ.
Справочное значение: 632,8 нМ.
Литература:
- Чарыев А. Основные законы физики. Учебное пособие для учителей средних и старших классов. — Ашхабад. Туркменская государственная издательская служба, 2004.
- www.phywe.com.
- info@phywe.com.

