Ключевые слова: ОЦК металл, ГЦК металл, ГПУ металл, кинетическая диаграмма усталостного разрушения, структурно-механическая модель разрушения
В настоящие момент изучению усталостной долговечности металлов с объемно-центрированной кубической решеткой (ОЦК) (рисунок 1) посвящены многие фундаментальные работы, которые позволяют на стадии проектирования и эксплуатации элементов конструкции провести детальный анализ особенностей её работы и принять меры по обеспечению её надёжности.
Рис. 1. Объемно-центрированная кубическая решетка
Развитие усталостного разрушения в металлах с гранецентрированной кубической решеткой (ГЦК) и гексагональной плотноупакованной решеткой (ГПУ) (рисунок 2), к которым относятся алюминий, медь, титан и т. д., изучено недостаточно плотно, следствием чего является отсутствие возможности определения ресурса сварных конструкций из металлов данного типа.
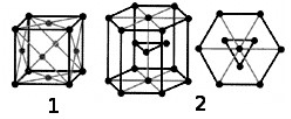
Рис. 2. Простые кристаллические решетки: 1 — гранецентрированная кубическая, 2 — гексагональная плотноупакованная
В связи с широким применением указанных металлов в различных областях промышленности, возникает необходимость в создании структурно– механической модели процесса разрушения металлов с гранецентрированной кубической и гексагональной плотноупакованной решетками. Существует некоторая вероятность того, что имеющиеся модели разрушения металлов с объемноцентрированной кубической решеткой могут быть успешно применены к металлам с ГЦК и ГПУ-решетками.
В работе осуществляется оценка применимости имеющейся структурно–механической модели разрушения для металлов с гранецентрированной кубической решеткой и гексагональной плотноупакованной решеткой. Указаны методы адаптации существующей модели.
Одним из этапов оценки применимости структурно–механической модели является определение истинной величины структурного элемента для каждого рассматриваемого материала. Обязательным условием для этого является наличие механических характеристик материала и кинетических диаграмм усталостного разрушения (КДУР).
Кинетические диаграммы усталостного разрушения позволяет определить характеристики циклической трещиностойкости [4]. Методика построения КДУР чётко регламентирована. Кинетические диаграммы позволяет проводить не только качественное, но и количественное сравнение данных о трещиностойкости различных конструкционных сталей.
Определяем величину структурного элемента с помощью программой «Ресурс». Программа «Ресурс» является реализацией алгоритма, представленного в книге Матохина Г. В., Горбачева К. П. «Инженеру о сопротивлении металлов разрушению» [1].
Параметры программы позволяют построить Кинетическую диаграмму усталостного разрушения материала при заданных параметрах.
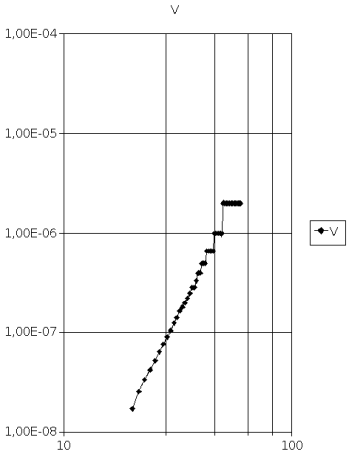
Рис. 3. Расчётная КДУР титанового сплава ВТ3–1, при dстр = 0,0028 мм
При сравнении расчётной и экспериментальной кинетических диаграмм усталостного разрушения заметно, что расчётные диаграммы 4 наиболее точно попадает в область экспериментальных значений, что означает верность подобранной величины структурного элемента.
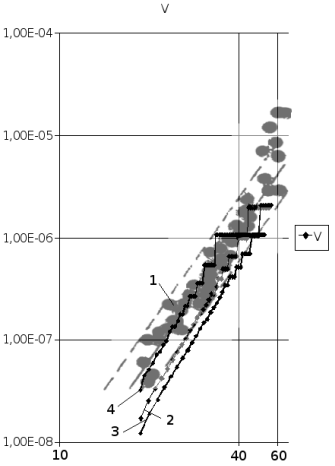
Рис. 4. КДУР титанового сплава ВТ3–1: 1 — экспериментальные данные; 2 — расчётная кривая при dстр = 0,0028 мм; 3 — расчётная кривая при dстр = 0,0038 мм; 4 — расчётная кривая при dстр = 0,0018 мм
Цель работы апробация использования имеющейся структурно– механической модели разрушения к с для гранецентрированной кубической и гексагональной плотноупакованной решеткой. Вследствие того, что данная структурно–механическая модель [1] была разработана для металлов с объемно-центрированной кубической решеткой, имелась вероятность того, что её применимость для металлов с гранецентрированной кубической и гексагональной плотноупакованной решеткой даёт неудовлетворительные результаты, так как в данной структурно–механической модели присутствует ряд допущений, присущих феррито-перлитным сталям.
В ходе выполнения работы была разработана методика оценки применимости структурно–механической модели к металлам с гранецентрированной кубической и гексагональной плотноупакованной решеткой. Методика заключается в определении величины структурного элемента, верность которого определяется совпадением экспериментальной и расчётной кинетических диаграмм усталостного разрушения.
Расчёт привел к следующим результатам. Были определены величины структурного элемента для титановых сплавов, при которых расчётная кинетическая диаграмма усталостного разрушения совпала с экспериментальной, что означает верность подобранной величины. Для алюминиевых и магниевого сплавов определение величины структурного элемента в данный момент невозможно, так как отсутствуют необходимые механические характеристики, а именно относительное сужение.
Из сказанного выше, можно сделать вывод, что имеющаяся структурно– механическая модель разрушения применима для титана и титановых сплавов. Вероятно, применима для металлов с гранецентрированной плотноупакованной решеткой. Оценить применимость модели к металлам с гранецентрированной кубической решеткой сложно, так как не были проведены соответствующие исследования, вследствие отсутствия необходимых данных.
Литература:
- Матохин Г. В. Оценка ресурса сварных конструкций из феррито-перлитных сталей. — Владивосток: ДВГТУ, 2001. — 202 с.
- Матохин Г. В., Горбачев К. П., Воробьев А. Ю. Основы оценки прочности и долговечности сварных конструкций. — Владивосток: ДВГТУ, 2008. — 300 с.
- Мешков Ю. Я., Пахаренко Г. В. Структура металла и хрупкость стальных изделий. — Киев: Наук. думка, 1985. — 268 с.
- Мешков А. А., Мовсун-Заде К. А., Дащенко А. Ф. Остаточный ресурс изделий с трещиной. — УДК 620.178:621.8, 5 с.

