Логарифмическая спираль в технике и в природе

Применения логарифмической спирали в технике основаны на свойстве этой кривой пересекать все свои радиусы-векторы под одним и тем же углом. Так, например, вращающиеся ножи в различных режущих машинах имеют профиль, очерченный по дуге спирали, благодаря чему угол резания, т. е. угол θ между лезвием ножа и направлением скорости его вращения, остается равным 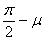 и, следовательно, неизменным в силу постоянства угла μ. В зависимости от обрабатываемого материала требуется тот или иной угол резания, что обеспечивается выбором параметра соответствующей спирали. На рис. 1 представлен нож соломорезки.

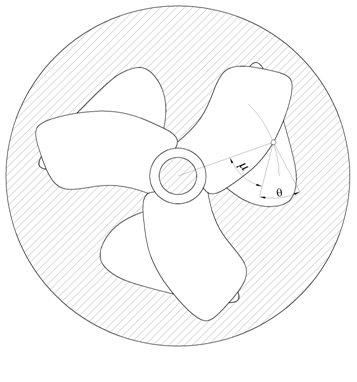
Рис. 1.

В гидротехнике по логарифмической спирали завертывают трубу, подводящую ток воды к лопастям турбинного колеса. Постоянство угла μ обеспечивает здесь то, что потери энергии на изменение, и следовательно, напор воды используется с максимальной производительностью.

В теории механизмов логарифмическая спираль применятся при проектировании зубчатых колес с переменным передаточным числом. Суть дела здесь такова: пусть два квадрата расположены так, как показано на рис. 2; через середину и конец каждой стороны этих квадратов проведены дуги одинаковых логарифмических спиралей с полюсами а центрах квадратов, одна из которых закручивается по ходу часовой стрелки, а другая — против; в точке Р спирали касаются между собой. Нетрудно показать, что при вращении квадратов вокруг их центров дуги спиралей будут катиться одна по другой без скольжения. Действительно, пусть М и М_1 — две точке спиралей, взятые так, ОМ+О₁М₁=ОР+О₁Р, или в иных обозначениях

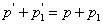                                                                                                             (1)

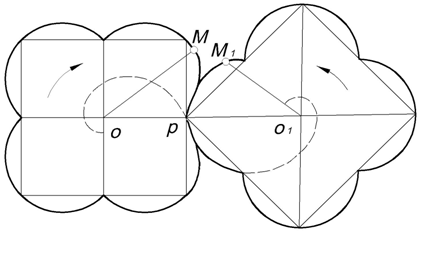
Рис. 2.

Очевидно, для качения без скольжения необходимо, чтобы

PM=PM₁                                                                                                                                                                (2)

но 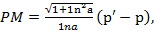 а 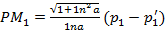, из равенства же (1) следует 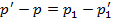, и, значит, равенство (2) действительно имеет место. Передаточное число, т. е. отношение угловых скоростей логарифмических колес, будет непрерывно меняться, достигая в течение каждого оборота колеса четыре раза максимального значения и четыре раза минимального.

Рис.

Рис. 4

Рис. 5.

В природе логарифмической спирали очерчены некоторые раковины (например, haliotis splendes, рис. 3). В подсолнухе семечки расположены по характерным дугам, близким, как показывают соответствующие измерения, к дугам логарифмической спирали. В связи с подобными фактами некоторые исследователи считают логарифмическую спираль кривой, в частности галактика, которой принадлежит солнечная система (рис. 4 и 5).

Литература:

1.                 Зенкевич И. Г. Эстетика урока математики. Пособие для учителей. — Москва: Просвещение, 1981.

2.                 Савелов А. А. «Плоские кривые» систематика, свойство, применения. — Москва: 1960 г.

3.                 Перевод с англ. А. М. Голова. Тайны живой природы. — М.: Росмэн, 2002 г.