Применение фракталов в медицине



Человеческое тело полно множества очень сложных структур. Например, грандиозное разветвление бронхов, некоторые части сердца, почечная система, большие кровеносные и капиллярные сети и т. д. Эти структуры, реальные физические системы, имеют геометрические и функциональные сложности. Точный подход к этим явлениям обязательно проходит через этап математического моделирования. Евклидова геометрия, к сожалению, не способна решить эти проблемы. На самом деле, это применяется только в случае гладких и правильных форм. Таким образом, точка имеет размерность, равную нулю, линия имеет размерность один, плоскость имеет размерность два, и объем имеет размерность, равную трем. Фрактальная же геометрия имеет дело с размерами, например, от одного до двух или от двух до трех и т. д. Фрактальная размерность фактически является размером нерегулярных кривых [1]. Данная специфика фракталов предоставляет нам огромные преимущества в области биологии и медицины при их использовании.

Действительно, многие сложные структуры живых систем и, в частности, человеческого тела проявляют фракталоподобную геометрию, что позволяет моделировать их и, следовательно, производить количественную оценку этих явлений с помощью фрактального анализа [2]. Наука о фрактальных объектах использует конкретные математические объекты неевклидовой геометрии.

Фрактал — это локализованный объект в пространстве, который можно разложить на все большее число похожих или идентичных элементов, которые становятся все меньше. Он является самоподобным объектом, а это значит, что его наименьшие элементы являются копиями его наибольших объектов. Для большинства фракталов, встречающихся в природе (границы облаков, линия берега, деревья, листья растений, кораллы и т. д.), более мелкие элементы похожи на более крупные, но не идентичны. Именно такие фрактальные объекты и получили название квазифракталов — они отличаются от идеальных абстрактных фракталов неполнотой и неточностью повторений структуры. Природные структуры не могут быть идеальными фракталами из-за ограничений, накладываемых размерами живой клетки и, в конечном итоге, размерами молекул.

Фрактальная размерность является показателем сложности кривой. Анализируя чередование участков с различной фрактальной размерностью и тем, как на систему воздействуют внешние и внутренние факторы, можно научиться предсказывать поведение системы. И что самое главное, диагностировать и предсказывать нестабильные состояния [3].

Одним из наиболее широко используемых методов измерений фракталов является размерность Минковского. Его популярность во многом обусловлена относительной простотой математического расчета. Пусть — любое непустое ограниченное подмножество в . Нижний и верхний пределы подмножества соответственно определены:

. (1)

Их так же еще называют верхней и нижней размерностями Минковского. Если они равны, то общее значение называется размерностью Минковского из и обозначается:

. (2)

Размерность Минковского имеет так же другое название — box-counting dimension, из-за альтернативного способа ее определения, который дает подсказку к способу вычисления этой самой размерности. Рассмотрим двумерный случай, хотя аналогичное определение распространяется и на n-мерный случай. Возьмем некоторое ограниченное множество в метрическом пространстве, например, черно-белую картинку, нарисуем на ней равномерную сетку с шагом , и закрасим те ячейки сетки, которые содержат хотя бы один элемент искомого множества (рисунок — 1).

Рис. 1. Вычисление размерности Минковского для двумерного случая

Далее начнем уменьшать размер ячеек, т. е. , тогда размерность Минковского будет вычисляться по вышеприведенной формуле, исследуя скорость изменения отношения логарифмов [4].

В этой статье будет рассмотрено одно из важных применений фракталов — применение в медицинской сфере. Поскольку фрактальная геометрия описывает морфогенетические законы сложных структур, еще 20 лет назад было предположено, что эти законы могут использоваться для математического моделирования формирования ретинальных сосудов (нормальной васкуляризации сетчатки) во время развития и в разработке автоматических методов диагностики заболеваний сетчатки, в том числе диагностики диабетической ретинопатии (ДР), очень распространенного и грозного осложнения болезни диабета.

В сетчатке, при развитии болезни фрактальные анатомические структуры, так же, как и другие фрактальные структуры в теле человека, изменяют степень своей сложности [5].

На рисунке 2 показаны здоровая и больная сетчатки.

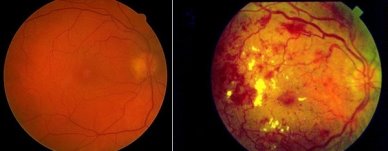
Рис. 2. Слева — здоровая сетчатка; справа — сетчатка, больная диабетической ретинопатией.

Диабетическая ретинопатия — это повреждение сосудов сетчатки у людей с сахарным диабетом. Патогенез ДР характеризуется следующими факторами (в зависимости от степени болезни): изменение калибра сосудов, извитость венозных петель капилляров, микроаневризмы, новообразования крупных сосудов с разрастанием соединительной ткани, прорастание соединительной ткани, прорастание сосудов в стекловидное тело, характерны кровоизлияния в различные отделы глаза, часто происходит отслойка и разрыв сетчатки. Это состояние развивается бесшумно и бессимптомно на протяжении многих лет. Только регулярный скрининг-тест мог бы диагностировать такие изменения в зачаточном состоянии. Обратите внимание, что диабетическая ретинопатия является основной причиной слепоты у людей с диабетом. Это заболевание поражает до 80 % всех пациентов с диабетом в течение 10 и более лет. Несмотря на эту пугающую статистику, исследования показывают, что по крайней мере на 90 % эти случаи можно было бы уменьшить, если бы пациенты своевременно получали адекватное лечение. Это показывает, какое значение имеет ранняя диагностика такого состояния. Обычная и классическая методика скрининга диабетической ретинопатии основана на исследовании глазного дна, которое проводится офтальмологом после расширения зрачка. Этот тип обследования легко понять, но он варьируется в зависимости от суждения лечащего врача, из-за чего значительная часть субъективности сохраняется, особенно в случаях ранних проявлений.

В последние десятилетия были опробованы новые методы скрининга диабетической ретинопатии. Методика фотографирования глазного дна без расширения зрачка с использованием цифровой камеры является наиболее актуальной. Это неинвазивный метод, который может быть выполнен техническим специалистом в течение короткого времени. Это позволяет делать цифровые фотографии, которые передаются в базу данных для тестирования.

Для обработки этих данных (изображений сетчатки) используется несколько методов. С учетом того, что вышеуказанные признаки ДР приводят к изменению структуры фракталов, методы, использующие фрактальный анализ — математический метод, позволяющий оценить степень сложности геометрии сосудистых сетей, по данным многих исследований являются наиболее последовательными и дают более точные результаты (рисунок 3) [5].

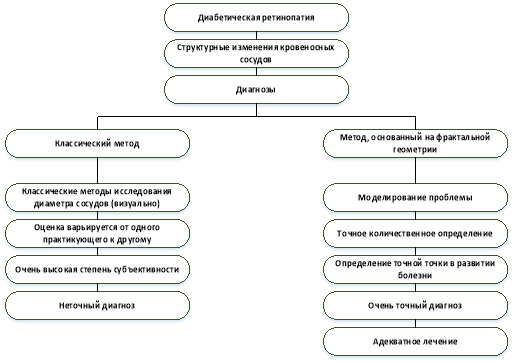
Рис. 3. Диагностика диабетической ретинопатии: огромный интерес к методу с использованием фракталов

Фрактальное измерение является основным инструментом фрактального анализа и одним из параметров, используемых для характеристики сложностей кровеносных сетей. Основываясь на оценке фрактальной размерности, используя разные алгоритмы и разные методы, исследования механизма формирования сосудистой сети сетчатки дают впечатляющие результаты и, следовательно, новые и очень важные интерпретации.

В качестве примера взято несколько изображений сетчатки из базы данных медицинских изображений STARE. Первый образец, обозначенный как образец А, состоит из десяти изображений нормальных сетчаток; второй, обозначенный как образец В, содержит десять изображений патологических сетчаток [6].

Оценка рассчитанных результатов производится путем сравнения значений, полученных для двух образцов. Для каждой группы был выполнен расчет фрактальной размерности. Обозначим через значение этой фрактальной размерности. Он рассчитывается в программе ImageJ (или других, таких как Image Processing Toolbox). Данная программа может отображать, редактировать, анализировать, обрабатывать, сохранять и печатать 8-битные, 16-битные и 32-битные изображения. Она может считывать много форматов изображений, в том числе TIFF, GIF, JPEG, BMP, DICOM, FITS и RAW. Она многопоточная, поэтому трудоемкие операции, такие как чтение изображения, могут выполняться параллельно с другими операциями [7].

Программа может вычислить площади и статистические показатели пиксельных значений для выделенных областей на изображении, может измерять расстояния и углы, может создавать гистограммы плотности и рисовать профили линий. Она поддерживает стандартные функции обработки изображений, такие как управление контрастностью, повышение резкости, сглаживание, обнаружение границ и медианный фильтр. Основной направленностью работы пакета является анализ, исследование и разработка математических алгоритмов и методов обработки и визуализации изображения.

В качестве примера здесь указаны основные шаги обработки изображения:

Шаг 1:Считывание и отображение изображения.

Шаг 2:Оценка и аппроксимация значений пикселей фона.

Шаг 3:Аппроксимация и просмотр поверхности фона.

Шаг 4:Создание изображения с равномерным фоном.

Шаг 5:Повышение контраста изображения.

Шаг 6:Создание бинарного изображения.

Шаг 7:Определение числа объектов на изображении.

Шаг 8:Анализ изображения.

Шаг 9:Отображение матрицы меток как псевдоцветового индексного изображения.

Шаг 10:Измерение свойств объектов на изображении.

Шаг 11:Вычислении статистических данных об объектах на изображении [8].

В таблице 1 результаты расчетов фрактальных размеров сгруппированы для образца А нормальных случаев (изображения здоровой сетчатки).

Таблица 1

Значения фрактальной размерности для образца А.

Номер изображения	Изображение сетчатки
1	im0077.ah	1,578
2	im0081.ah	1,554
3	im0082.ah	1,578
4	im0162.ah	1,651
5	im0163.ah	1,641
6	im0235.ah	1,598
7	im0236.ah	1,585
8	im0239.ah	1,588
9	im0240.ah	1,594
10	Im0255.ah	1,634
Среднее значение		1,6

Форма распределения кровеносных сосудов сетчатки человека очень сложна и сильно отличается от человека к человеку, даже в случае нормальных сетчаток. Это значительно усложняет сравнение распределений этих сетей. При лечении патологических сетчаток сложность еще увеличивается. Именно геометрия фрактала может более точно характеризовать эти неправильные формы. Рисунок 4, извлеченный из базы данных STARE, показывает фрактальную форму распределения кровеносных сосудов нормальной сетчатки.

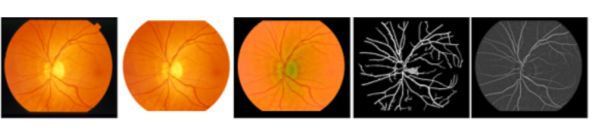
Рис. 4. Изображение нормальной сети сосудов сетчатки (файл im0163.ah)

Для образца А синяя линия на рис. 5 представляет фрактальное измерение, связанное с каждым нормальным случаем сетчатки человека. Эта кривая показывает более или менее линейный вид. Значения фрактальных размеров примерно одинаковы для десяти изученных случаев.

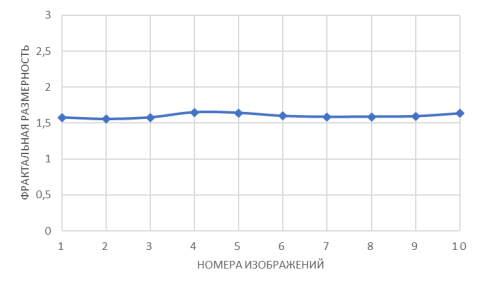
Рис. 5. График, связывающий значения фрактальной размерности с номерами изображений образца А (нормальные сетчатки)

В таблице 2 приведены результаты расчетов фрактальных размеров для образца В, содержащего патологические случаи (изображения больных сетчаток). Рисунок 6, полученный из базы данных STARE, выделяет надломленный вид структуры кровеносных сосудов патологической сетчатки.

Таблица 2

Значения фрактальной размерности для образца В

Номер изображения	Изображение сетчатки
1	im0001.ah	1,539
2	im0002.ah	1,549
3	im0003.ah	1,508
4	im0004.ah	1,522
5	im0005.ah	1,590
6	im0044.ah	1,540
7	im0139.ah	1,565
8	im0291.ah	1,519
9	im0319.ah	1,444
10	Im0324.ah	1,567
Среднее значение		1,53

Рис. 6. Изображение патологической сети сосудов сетчатки (файл im0003.ah)

В случае образца В, на рис. 7 красная линия показывает фрактальное измерение для каждого патологического случая. Легко заметить ломаную форму этой кривой. Она показывает изменение фрактальной размерности патологического субъекта по сравнению с другими. Это изменение связано с различной степенью поражения кровеносных сосудов сетчатки. Клинические признаки изменений размеров фракталов (рис. 6) очень важны, поскольку они позволяют очень точно классифицировать стадии разрушения сетчатки.

Рис. 7 показывает сравнение результатов для обоих образцов А и В. Хорошо видно, что фрактальный размер для образца В (патологические сетчатки) значительно ниже, чем для образца А (нормальные сетчатки).

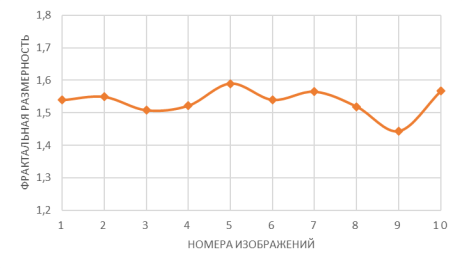
Рис. 7. График, связывающий значения фрактальной размерности с номерами изображений образца В (патологические сетчатки)

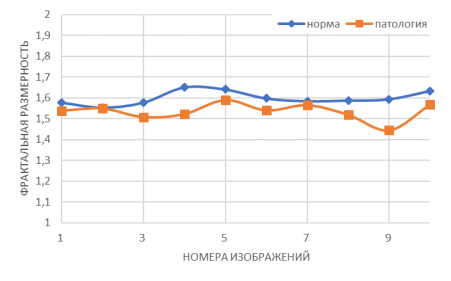
Рис. 8. Сравнение кривых фрактальных размерностей для образца А и для образца В

При интерпретации результатов надо учитывать, что фрактальная размерность сосудов сетчатки зависит также от других факторов, например, таких как возраст, сопутствующие заболевания.

Со статистической точки зрения увеличение числа случаев в каждой выборке может дать более убедительные результаты.

Подводя итоги, можно сказать, что так как сетчатка глаза человека имеет сложную сосудистую сеть, имеющую фрактальную структуру, то благодаря этому, фрактальная геометрия, в отличие от евклидовой геометрии, обеспечивает более точный метод моделирования сосудистой сети. Фрактальный анализ сосудистой сети, сформированной на изображениях сетчатки человека, может использоваться в качестве неинвазивного метода для выявления сосудистых заболеваний, в том числе диабетической ретинопатии, и способствовать своевременному выявлению и лечению заболеваний ещё на ранних стадиях.

Автоматизированный анализ фракталов также находит применение и в других областях, например, в компьютерной лазерной хирургии и в биометрической идентификации.

Литература:

1. Falconer K. J. Fractal Geometry: Mathematical Foundations and Applications. — New York: John Wiley Sons Inc., 1990.
2. Barnsley M. F. Fractals Everywhere. — Boston: Academic Press, 1988.
3. Фрактальная размерность // Forex: в помощь начинающему трейдеру. URL: https://help-on-forex.com/almazov15.html (дата обращения: 13.02.2019).
4. Вычисление фрактальной размерности Минковского для плоского изображения // habr. URL: https://habr.com/ru/post/208368/ (дата обращения: 13.02.2019).
5. Нелинейные фракталы: приложения в физиологии и офтальмологии. Обзор // DOCPLAYER. URL: https://docplayer.ru/26060813-Nelineynye-fraktaly-prilozheniya-v-fiziologii-i-oftalmologii-obzor.html (дата обращения: 13.02.2019).
6. Stosic T., Stosic B. D. Multifractal Analysis of Human Retinal Vessels, IEEE Transactions on Medical Imaging Volume. — 8-е изд., 2006.
7. ImageJ // ВикиПрограммы. URL: http://wikiprograms.org/imagej/ (дата обращения: 13.02.2019).
8. Обработка изображений в MATLAB // cyberpedia. URL: https://cyberpedia.su/11x95d.html (дата обращения: 17.02.2019).