Использование компьютерных программ в курсе геометрии



В 1954 году профессор Кембриджского университета Беррес Фредерик Скиннер сформулировал принципы изучения математики, грамматики и других предметов. Идея стала известна как теория программированного обучения. Позже Фредерик Скиннер представил обучающую машину для использования ее в школьном обучении [1]. Основываясь на теории программированного обучения, Дональд Битцер в 1960 году разработал компьютерную систему PLATO для обучения студентов тематическим курсам.

При обучении геометрии рассматривают различные фигуры. Программа, которую мы будем рассматривать в данной статье, позволяет строить и изменять любые геометрические фигуры по усмотрению учителя.

Использование компьютерных программ на уроках позволят детальнее рассматривать ту или иную геометрическую фигуру и более подробно объяснить теорему или аксиому. Чаще всего учителя для наглядности предпочитают изображать геометрические фигуры, чтобы лучше донести до учеников тему урока. Геометрия — сложный предмет, который не все могут постичь, а наиболее трудной частью являются пространственные фигуры, такие как цилиндр, призма, пирамида, конус, шар, параллелепипед, а также их усеченные версии. Компьютерные программы помогают учителю более доступно объяснить трудные темы на уроках геометрии. Изображая пространственную фигуру на доске, учитель не может показать ее с той или иной стороны, компьютерные программы позволяют демонстрировать фигуру с разных сторон.

Чаще всего на уроках геометрии используют такие программы, как PowerPoint, Mathcad, GeoGebra.

PowerPoint показывает слайды, способствующие решению задач, которые ставят на уроках геометрии [2]:

— развитие воображения и образного мышления;

— развитие логического мышления;

— формирование умения излагать свои мысли;

— совершенствование графической культуры.

Рис. 1. Пример рассмотрения геометрической фигуры в PowerPoint [3]

Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением. Она отличается легкостью в использовании и применяется для коллективной работы.

Основные плюсы Mathcad:

— универсальность (может быть использована для решения разнообразных задач);

— программирование на общепринятом математическом языке. Благодаря этому программа доступна и студентам, и академикам;

— совместное применение текстового редактора, формульного транслятора и графического процессора позволяет пользователю в ходе вычислений получить готовый документ;

— широкие возможности построения различных видов графиков, в явном и параметрическом виде, в декартовой, полярной, сферической системах координат, 3D-поверхностей и касательных поверхностей к ним [4].

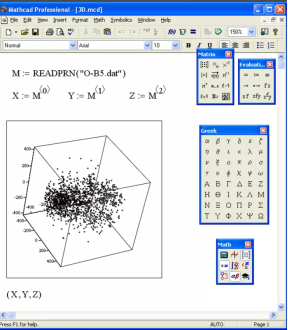
Рис. 2. Пример рассмотрения геометрической фигуры в Mathcad

Программа GeoGebra обладает стандартным интерфейсом и переведена на большинство языков мира. Она служит для подготовки наглядных пособий и помогает учителю на уроках геометрии [5].

Достоинства GeoGebra:

— поддержка нескольких языков;

— многофункциональность, в том числе при работе с графикой;

— личное комьюнити;

— поддерживается практически всеми ОС: Windows, OS X, Linux, Android и iOS [6].

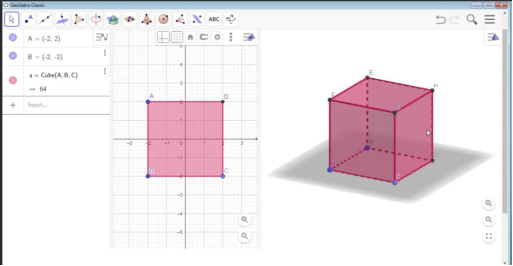
Рис. 3. Пример рассмотрения геометрической фигуры в GeoGebra

Программа Geometer's Sketchpad («Живая геометрия») разработана для использования в школьном курсе геометрии и алгебры. В программе можно создавать точные чертежи и графики, которые крайне трудно построить вручную на бумаге, строить привлекательные фракталы, заставить вращаться идеально правильные фигуры. Программа позволяет:

— создавать чертежи;

— анимировать их, плавно меняя положение исходных точек (мышкой или автоматически);

— измерять длину, ширину, высоту, площади и углы с выбранной точностью;

— создавать множество исследовательских и обучающих живых чертежей;

— использовать хранилища архивов чертежей.

И. В. Роберт выделяет следующие направления развития деятельности учащихся по мере приобретения навыков работы с программой:

— построение;

— исследование;

— анализ;

— рисование;

— доказательство;

— решение головоломок;

— решение задач.

Создатели «Живой геометрии» предусмотрели работу с ней в разнообразных условиях:

— в классе с одним компьютером;

— в классе с компьютером и мультимедиа-проектором или электронной доской;

— в классе с интернетом;

— в компьютерной лаборатории и т. д.

Использование программы дает несомненные преимущества по сравнению со стандартным стилем преподавания на уроках геометрии. Высокий эстетический уровень оформления программы делает изучение геометрии привлекательным и открывает возможности таких ее нетрадиционных приложений, как построение узоров, дизайн и т. п.

Достаточным (хотя далеко не исчерпывающим) основанием для ее активного внедрения в наши классы является естественная и мощная техника построения чертежей — аккуратных, грамотно описываемых и легко редактируемых [7].

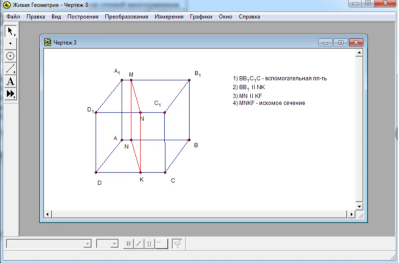
Рис. 4. Пример рассмотрения геометрической фигуры в Geometer's Sketchpad

Урок — основная форма организации учебно-воспитательного процесса, и качество обучения — это, прежде всего, качество урока. С использованием компьютерных программ урок становится богаче, ярче, образнее. С их помощью на учащихся оказывается эмоциональное воздействие, они способствуют лучшему запоминанию материала, повышают интерес к предмету, обеспечивают прочность усвоения знаний. Использование компьютерных программ позволяет увеличить темп обучения, учитывать различные каналы восприятия, дает возможность многократного повторения, активизирует лево-правополушарные способы восприятия информации учащимися. Также это экономит время — в среднем учитель тратит 1–3 минуты на изображение чертежа на доске. Если в кабинете имеется электронная доска, ученики могут изображать фигуры на ней.

Рассмотрим тему «Окружность, описанная около треугольника. Окружность, вписанная в треугольник».

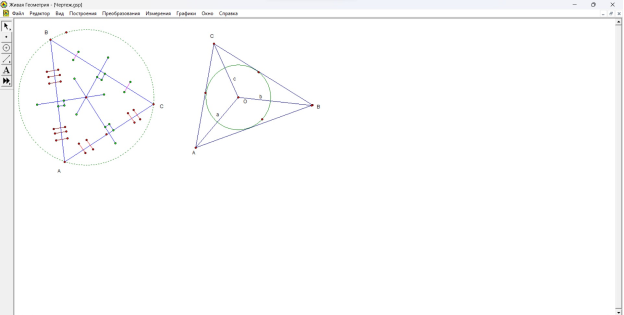
Рис. 5. Окружность, описанная около треугольника. Окружность, вписанная в треугольник

Окружность называется описанной около треугольника, если все вершины треугольника находятся на данной окружности. При этом окружность называется вписанной, если внутри треугольника находится окружность, и при этом три стороны треугольника соприкасаются с окружностью.

Построим фигуры на интерактивной доске с помощью программы Geometer's Sketchpad и назовем их. Запишем под каждым рисунком теорему.

Теорема.

Около всякого треугольника можно описать окружность. Ее центром является точка пересечения серединных перпендикуляров к сторонам треугольника [8].

Доказательство.

Рассмотрим треугольник АВС. К сторонам АВ и АС проведем серединные перпендикуляры b и c соответственно. Докажем, что точка О их пересечения является центром описанной окружности. Для этого достаточно проверить, что выполняются равенства ОА = ОВ = ОС.

Действительно, так как точка О принадлежит серединному перпендикуляру с к отрезку АВ, то она одинаково удалена от вершин А и В, т. е. ОА = ОВ. Так как точка О принадлежит серединному перпендикуляру b к отрезку АС, то она одинаково удалена от вершин А и С, т. е. ОА = ОС.

Следовательно, точка О одинаково удалена от вершин А, В, С треугольника АВС, т. е. ОА = ОВ = ОС. Заметим, что из равенства ОВ = ОС следует, что точка О принадлежит серединному перпендикуляру а к стороне ВС. Таким образом, все три серединных перпендикуляра пересекаются в одной точке О. Окружность с центром в этой точке и радиусом R = ОА = ОВ = ОС будет искомой описанной окружностью.

Теорема.

В любой треугольник можно вписать окружность. Ее центром является точка пересечения биссектрис этого треугольника.

Доказательство.

Рассмотрим треугольник АВС и из его вершин А и В проведем биссектрисы а и b соответственно. Докажем, что точка О их пересечения является центром вписанной окружности. Для этого достаточно проверить равенство перпендикуляров OD, OE и OF, опущенных из точки О на стороны треугольника АВС, или, что то же самое, что точка О одинаково удалена от сторон треугольника АВС.

Действительно, так как точка О принадлежит биссектрисе а , она одинаково удалена от сторон АВ и АС. Так как точка О принадлежит биссектрисе b , то она одинаково удалена от сторон АВ и ВС. Значит, точка О одинаково удалена ото всех сторон треугольника АВС. Заметим, что из того, что точка О одинаково удалена от сторон ВС и АС следует, что она принадлежит биссектрисе с угла С, т. е. все три биссектрисы пересекаются в одной точке О. Окружность с центром в этой точке и радиусом r = OD = OE = OF будет искомой вписанной в треугольник окружностью.

Таким образом, мы можем сделать вывод, что использование компьютерной программы на уроках геометрии крайне положительно скажется на усвоении знаний, касающихся трудных геометрических фигур. Также они помогут более наглядному представлению темы, что облегчит ее понимание обучающимися.

Литература:

1. https://habr.com/ru/companies/spbifmo/articles/476160/
2. Старцева Н. А. Применение электронных пособий на уроках математики. Информационные технологии в образовании : сб. научно-методических материалов. Новосибирск : НГУ, 2004.
3. Савченко Е. М. Уроки геометрии с применением информационных технологий. 7–9 классы. Методическое пособие с электронным приложением. — М. : Планета, 2011.
4. Колпакова, Д. С. GeoGebra как средство визуализации решения задач на уроках геометрии в 7 классе / Д. С. Колпакова. — Текст: непосредственный // Молодой ученый. — 2018. — № 11 (197). — С. 164–167. — URL: https://moluch.ru/archive/197/48799/ (дата обращения: 03.11.2023).
5. https://public-pc.com/geogebra-an-overview/
6. Математика. — Издательский дом 1 сентября. № 15. 2008.
7. Смирнов В. А., Туяков Е. А. Геометрия. Учебник для 9 кл. общеобразоват. шк. Алматы: мектеп, 2019. 176 с., илл.