Практическое применение геометрии



Математик, который не является отчасти поэтом, никогда не достигнет совершенства в математике.

К. Вейерштрасс

Замечательные точки треугольника — точки, местоположение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника. Обычно они расположены внутри треугольника, но и это не обязательно.

С каждым треугольником связаны четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения высот, точка пересечения серединных перпендикуляров.

В своей работе я рассмотрю свойства точек пересечения биссектрис, медиан, рассмотрю серединный перпендикуляр, расскажу о замечательных их свойствах и линиях треугольника. К числу таких точек, изучаемых в школьном курсе геометрии, относятся: точка пересечения биссектрис (центр вписанной окружности), точка пересечения серединных перпендикуляров (центр описанной окружности), точка пересечения медиан (центроид).

За годы обучения в художественной школе я поняла, что для меня очень актуальна тема построения предметов, современное искусство, современная архитектура построена на фундаментальных знаниях о геометрических фигурах. Ведь даже для того, чтобы нарисовать правильно лицо человека, нужно знать основы построения геометрических фигур. Вот, например, фрагмент из книги «Портреты карандашом. Техники достижения фотореализма» Е. Матита (Рис.1). Рисуем нос человека. И мы видим, что сначала надо нарисовать окружность, потом вторую окружность, горизонтальные, вертикальные линии, перпендикуляры и прочее. А это все будет возможно только, если я буду знать, как построить круг, квадрат, перпендикуляр и т. д.. И, заметьте, все это я рисую от руки, без циркуля и линйки. Поэтому тема «Замечательные точки треугольника» для меня очень важна.

Рис. 1

1.1. Цель работы

Цель: исследование треугольника на его замечательные точки, изучение их классификаций и свойств, применить на практике их свойства.

1.2. Задачи работы

1. Изучить необходимую литературу.
2. Рассмотреть свойства биссектрис, медиан, серединных перпендикуляров и высот треугольника, сформулировать и доказать теоремы.
3. Уметь строить замечательные точки треугольника.
4. Найти практическое применение замечательных точек треугольника
5. Обобщить изученный материал для оформления проекта.
   3. Актуальность работы

Актуальность: расширить свои знания о треугольнике, свойствах его замечательных точек. В пункте об актуальности данной темы, я хочу представить часть своих работ, для наглядного отображения всей значимости данной темы (Рис. 2, 3, 4, 5, 6, 7):

Рис. 2

Рис. 3

Рис. 4

Рис. 5

Рис. 6

Рис. 7

Этими рисунками я хотела сказать, что для того, чтобы нарисовать полноценную картину как на рисунке 8, надо научиться строить геометрические фигуры как на рисунках 1,2,3,4,5,6,7. Рисунками 9,10,11,12 хочу показать геометрию в теле человека.

2. Практическая часть изучения точек треугольника.
   1. Биссектриса угла

Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам.

Свойства биссектрисы угла: любая точка биссектрисы угла треугольника равноудалена от сторон этого угла.

Теорема 1: Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла. (рис.8)

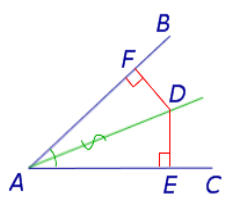
Рис.8

Теорема 2 :(обратная теорема к теореме 1). Если некоторая точка находится на одном и том же расстоянии от сторон угла , то она лежит на биссектрисе угла (рис.9).

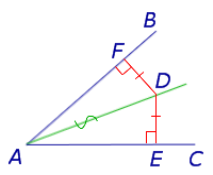
Рис. 9

2.2. Биссектриса треугольника

Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.

Свойства биссектрис треугольника:

1. Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.
2. Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.

Теорема 3 : В любом треугольнике все три биссектрисы пересекаются в одной точке.

Следствие: биссектрисы треугольника пересекаются в одной точке (рис. 10). И это наша первая замечательная точка.

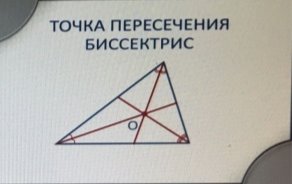
Рис. 10

Замечательно то, что если взять три произвольные точки пространства (рис. 11), построить из них треугольник произвольный (рис.12), провести биссектрисы (рис.13), биссектрисы пересекутся в одной точке! Казалось бы, это невозможно, потому что мы взяли произвольные точки, но это правило действует всегда.

Рис. 11

Рис. 12

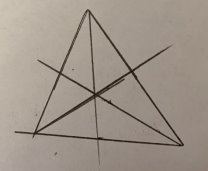
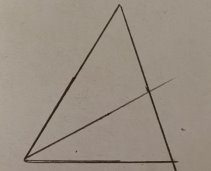
Рис. 13

А теперь, имея только транспортир или линейку, мы можем построить, не имея в наличии циркуля, круг, нужного нам размера из трех произвольных точек (рис. 14). Найдем наименьший отрезок биссектрисы от точки пересечения биссектрис с точкой на противоположной стороне треугольника — этот отрезок и будет являться радиусом нашей окружности. Отмерим этот отрезок на остальных биссектрисах и нарисуем наш ровный круг от руки.

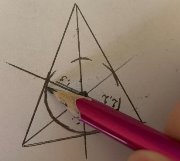
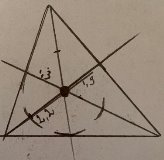
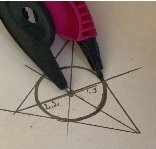
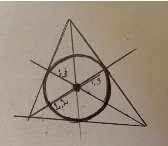
Рис.14

Проверим циркулем — круг ровный !

2.3. Серединный перпендикуляр

Вторая замечательная точка треугольника — точка пересечения серединных перпендикуляров сторон треугольника.

Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему (рис.15)

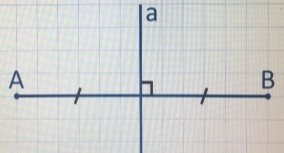
Рис. 15

Свойства серединных перпендикуляров треугольника:

Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника (рис.16)

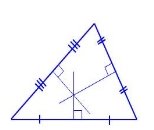
Рис.16

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка (рис.17)

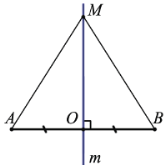
Рис.17

Верна и обратная теорема.

Теорема: Каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему (рис. 18).

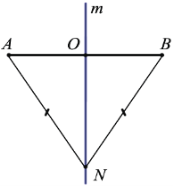
Рис. 18

Рассмотрим следствие серединного перпендикуляра к сторонам треугольника в рис. 19.

Рис. 19

Точка пересечения серединных перпендикуляров к сторонам треугольника — замечательная точка треугольника, так как она является центром окружности, описанной около треугольника. Что нам дают эти знания? А то, что благодаря нарисованному треугольнику, и проведя в нем серединные перпендикуляры, мы можем легко, без помощи циркуля описать вокруг него окружность:

Строим произвольный треугольник (Рис. 20)

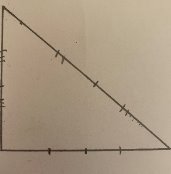
Рис. 20

Проводим серединные перпендикуляры (Рис. 21)

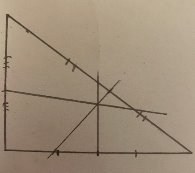
Рис. 21

Отмечаем точку пересечения серединных перпендикуляров (центр нашей бедующей окружности) (Рис. 22)

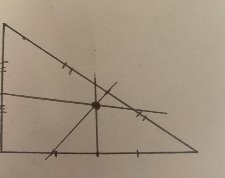
Рис.22

Начинаем строить наш круг (Рис. 23):

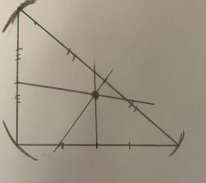
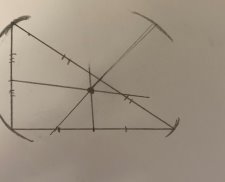
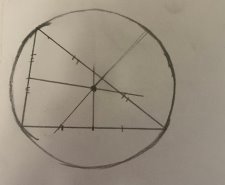
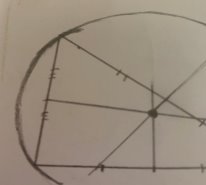
Рис.23

2.4. Медиана треугольника

Третья замечательная точка треугольника — точка пересечения медиан.

Медиана треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис. 24)

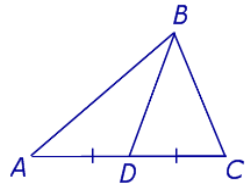
Рис. 24

Основные свойства медиан треугольника:

– Медианы треугольника точкой их пересечения делятся в отношении 2:1 (считая от вершины треугольника).

– Медиана делит треугольник на два равновеликих треугольника. (Два треугольника равновелики, если их площади равны).

Точка пересечения медиан — это центр тяжести треугольника (Рис. 25), и это очень важное свойство этой точки, которое может помочь при проектировании современных архитектурных сооружений, ведь зная, что точка пересечения медиан в треугольнике — это его барицентр, можно проектировать сложные геометрические композиции в интерьере.

Рис. 25

Все мы помним сувенир — «Орел на пирамиде» (Рис. 26).

Рис. 26

Эта же игрушка сделана из легкого пластика. Одна единственная точка опоры и тело, расположенное перпендикулярно земле.

На первый взгляд кажется, что все это какой-то технический или визуальный фокус, и все это очень эфемерно, и рухнет сразу же, стоит только задеть. Но на самом деле, конструкция весьма надежна, может быстро вращаться вокруг собственной оси, да и сбросить птичку с постамента не так легко. Устойчивость потрясающая.

Пирамидка на самом деле не играет в этом трюке никакой роли. Птицу можно прицепить на палец, или на карандаш, да хоть куда угодно.

Все дело в том, что центр тяжести птички приходится аккуратно на клюв. Сделана игрушка из легкого материала. Внутрь крыльев вставлены металлические утяжелители, которые и создают противовес телу птицы. Это, конечно не треугольник, но суть центра тяжести именно в этом. А «Орла на пирамиде» видели все, и более яркого примера для цента тяжести не придумаешь.

На рисунке 27 изображен проект современного торгового комплекса, и мы видим, что он состоит из треугольных фигур, прочность данной конструкции, может быть обеспечена только, если мы четко будем понимать, что центр тяжести каждого треугольника находится на твердой основе, и тогда его свободный край никогда не упадет.

Рис.27

3. Вывод

В результате выполнения данной работы мною былирассмотрены свойства биссектрис, медиан, серединных перпендикуляров и высот треугольника, расширено число замечательных точек и линий треугольника, сформулированы и доказаны теоремы, что в дальнейшем поможет нам при решении ряда задач на применение этих теорем.

Я научилась находить и строить замечательные точки треугольника.

Мною было изучено много материала по данной теме, в результате чего я выделила основное и оформила в данный проект. Я научились находить практическое применение основ геометрии в повседневной жизни.

4. Заключение

В данной работе я рассмотрела 4 замечательные точки треугольника. Полученные знания по данной теме я смогу использовать в своей учебной деятельности, самостоятельно применять теоремы к определенным задачам, применять изученные теоремы в реальной ситуации. Я много говорила о построении круга, зная свойства разных прямых в треугольнике, в заключении темы я хочу показать пример рисования собаки, с помощью тех приемов, которые были изложены выше (Рис. 28)

Думаю, каждый сможет нарисовать данное животное, и для этого нам надо знать всего лишь основы построения геометрических фигур.

Рис. 28.