Математическая модель нарушений функционирования щитовидной железы

Разработана математическая модель функционирования щитовидной железы, представляющая собой задачу Коши для системы обыкновенных дифференциальных уравнений. Учитываются возможные нарушения ее функций. Предлагаются варианты планирования лечения, позволяющие оценить как время лечения, так и экономические затраты.

Ключевые слова: математическое моделирование, дифференциальные уравнения, щитовидная железа.

Введение. Щитовидная железа в организмах млекопитающих несет функциональную нагрузку, связанную с развитием организма. В ней перерабатывается жизненно необходимый йод, вырабатываются гормоны, регулирующие различные биохимические реакции и определяющие нормальное функционирование организма. Нарушения ее работы приводят к нарушению обменных процессов в организме и возникновению различных йододефицитных заболеваний. В опубликованных в литературных источниках математических моделях [1-4] описывается, как правило, йодный обмен в организме, а не работа самой железы. Наиболее полная математическая модель щитовидной железы, предложенная в [5] как элемент эндокринной системы, представляет собой систему десяти обыкновенных дифференциальных уравнений, содержащую более 50 констант. При таком количестве переменных и констант определение последних из экспериментальных данных представляет собой не простую задачу, возможно и не разрешимую. Синтез и освобождение гормонов являются сложными процессами, включают в себя множество различных биохимических реакций. В предложенной авторами работе [6] математической модели фолликула щитовидной железы учитываются основные реакции, протекающие в нем: поступление йода, связывание его с тиреоглобулином с последующим образованием и накоплением в нем гормона 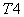 [7-9]. Модель представляет собой задачу Коши для системы четырех обыкновенных дифференциальных уравнений.

Основные биохимические реакции. Щитовидная железа в модели представляется, как и фолликул [8], двухслойным шарообразным телом. Внешний (первая камера) и внутренний (вторая камера) слои разделены мембраной. Во внешний слой через его внешнюю поверхность поступает йод (I), который после связывания с находящимся в этом слое тиреоглобулином (Tg), поступает во внутренний слой через разделительную мембрану, проницаемость которой 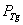. Йод во внутренний слой не поступает. Во внутреннем слое тиреоглобулин участвует в реакции образования гормона (Т4), который хранится в связанном с тиреоглобулином виде. При снижении уровня гормона в сыворотке крови гормон отщепляется от тиреоглобулина и из щитовидной железы в свободном виде попадает в кровоток через внешнюю мембрану с проницаемостью  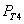[7, 10 – 12]. Тиреоглобулин сохраняется в железе, во внешнюю среду не поступает.

Математическая модель. При построении математической модели используются подходы, аналогичные примененным в [1-5]. Пусть

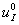 – концентрация йода во внешнем потоке, поступающем в первую камеру со скоростью ;

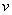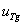 – концентрация тиреоглобулина в первой камере;

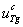 – концентрация тиреоглобулина во второй камере;

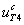 – концентрация гормона  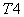во второй камере;

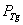 – проницаемость разделительной между камерами мембраны для тиреоглобулина;  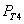– проницаемость разделительной между камерами мембраны для гормона .

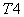С учетом введенных обозначений реакции, протекающие в первой камере, описываются уравнениями

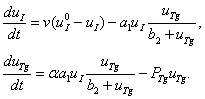                                                                                    (1)

Слагаемое 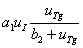 в первом уравнении – скорость связывания йода и тиреоглобулина, а слагаемое  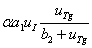во втором уравнении – скорость образования тиреоглобулина. Слагаемое  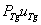во втором уравнении описывает скорость убыли тиреоглобулина через мембрану коллоида с проницаемостью  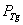для тиреоглобулина в коллоид.

Реакции, проходящие во второй камере, описываются уравнениями

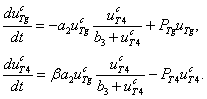                                                                                   (2)

В первом уравнении слагаемое 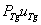 есть скорость поступления тиреоглобулина из первой камеры во вторую, слагаемое  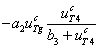– скорость расхода тиреоглобулина во второй камере на образование гормона, слагаемое  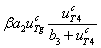– скорость образования гормона, а слагаемое  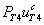– скорость перехода гормона  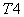в кровоток через мембрану коллоида с проницаемостью  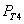для гормона. В уравнениях (1) – (2) 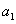, , 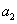, , 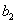,  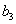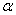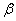– положительные постоянные.

Стационарные точки. Система уравнений (1) – (2) имеет стационарную точку 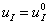, 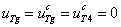. Стационарные точки будут устойчивыми, если собственные значения матрицы Якоби правой части уравнений (1) – (2) имеют отрицательные вещественные части [13]. Собственные значения матрицы Якоби уравнений (2) в этой точке равны 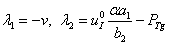. При выполнении неравенства  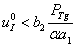эта точка будет устойчивой.

Вторая стационарная точка удовлетворяет системе уравнений

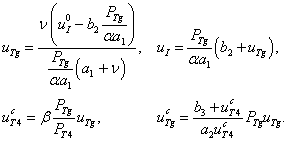                                                               (3)

Физический смысл эта точка имеет при выполнении неравенства

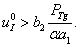                                                                                                                   (4)

Четыре собственных значения матрицы Якоби правой части системы уравнений (1) – (2) являются корнями квадратных уравнений

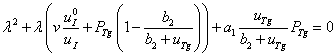,                                                  (5)

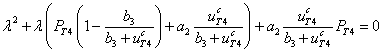.                                      (6)

Как следует из анализа уравнений (5) – (6), в стационарной точке (3) собственные значения будут либо отрицательными, либо иметь отрицательные вещественные части. Т.е., при выполнении условия (4) это стационарное состояние будет устойчивым.

С учетом опубликованных в литературных источниках относительных значений констант [1, 5], входящих в уравнения (1) – (2), в модели принято – 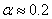, , 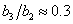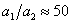. Остальные константы выбирались из условий обеспечения заданных выходных характеристик на основании соотношений (3): конверсия йода составляет 90%, а на выходе отношение концентрации гормона к концентрации тиреоглобулина равно 4:1 [14, 15, 16]. За единичную принималась константа 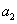. С учетом этого, в модели было принято: 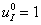, , 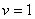, , 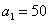, , 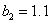, 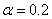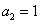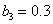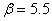. При принятом наборе констант единица измерения времени в модели соответствует суткам, а концентрации веществ считаются безразмерными.

Нарушение работы щитовидной железы. Нарушения могут происходить по внутренним и внешним причинам. К числу внутренних причин можно отнести, прежде всего, изменение скоростей реакций и механических характеристик системы, изменение свойств внешней и внутренней мембран. Внешними причинами являются изменение поступающего извне йода и воздействие различных вредных веществ [17], влияющих на протекание биохимических реакций в организме [18, 19].

Одним из основных нарушений является изменение количества поступающего в железу йода. Согласно соотношениям (3) это сопровождается увеличением или уменьшением выхода гормона. Восстановить ее нормальные свойства можно за счет внешнего воздействия (лечения [20]). Рассматриваются два варианта. В первом варианте воздействие начинается в момент начала нарушения (ранняя диагностика), во втором – после достижения максимального нарушения (поздняя диагностика).

Пусть в щитовидную железу поступает дополнительный йод в количестве 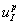, выводящий ее из стационарного состояния. Изменение его количества происходит за счет введения препаратов концентрации 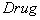. Модель функционирования щитовидной железы (1) – (2) с учетом этих нарушений примет следующий вид:

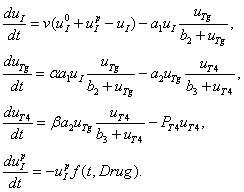                                                                          (7)

В этих уравнениях 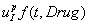 – скорость уменьшения концентрации дополнительного йода за счет введенных препаратов. Предполагается, что эта скорость пропорциональна количеству введенных препаратов и количеству дополнительного йода. Препараты вводятся на промежутке времени  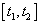по закону 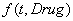. Общее количество вводимых препаратов подсчитывается по формуле 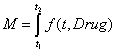. В качестве функций  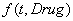рассматриваются два варианта:

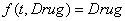;                                                                                                       (8)

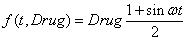.                                                                                       (9)

Первый вариант соответствует случаю, когда дозировка препарата постоянна, второй вариант соответствует случаю, когда дозировка препаратов меняется во времени.

В качестве начальных условий рассматриваются два варианта. В первом в момент времени 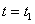 система находится в стационарном положении равновесия, описываемого соотношениями (3). При этом в этот момент времени происходит нарушение работы щитовидной железы, так что количество дополнительного йода 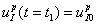. В этот же момент времени начинает подаваться препарат. Этот случай моделирует раннюю диагностику нарушения работы железы. Во втором варианте предполагается, что в момент времени  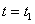система находится в стационарном положении равновесия, описываемого соотношениями (3) при концентрации поступающего йода равной 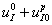. Это случай позднего обнаружения нарушения. Расход препаратов в первом случае ((8)) определяется как 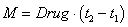, а во втором ((9))

.

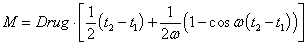Результаты численного моделирования (решение уравнений (7)) для случая 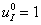, , 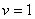, 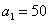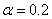; ; 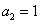; ; 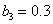;  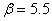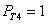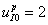представлены на рис. 1 – 2.

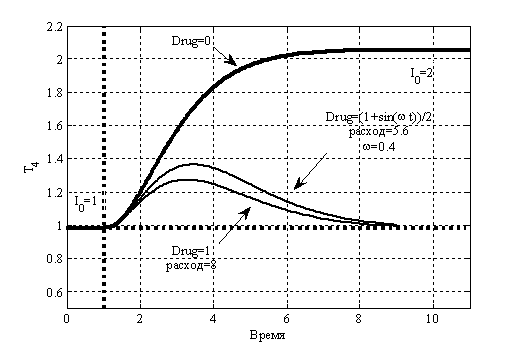
Рис. 1. Влияние лекарственных препаратов на выход гормона Т4 (ранняя диагностика).

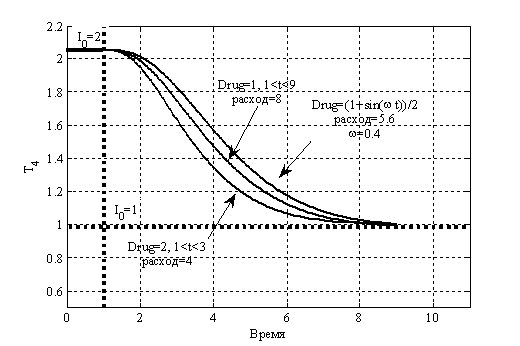
Рис. 2. Влияние лекарственных препаратов на выход гормона Т4 (поздняя диагностика).

Для случая ранней диагностики изменение выхода гормона Т4 представлено на рис. 1. Кривая 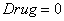 соответствует нарушенному выходу гормона в случае отсутствия воздействия препаратами; кривая  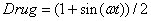соответствует варианту введения препаратов с переменной дозировкой; кривая  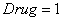соответствует варианту введения препаратов с постоянной дозировкой. Время подачи препаратов 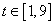. Расход препарата в первом случае составил 5.6 единиц, а во втором – 8 единиц.

На рис. 2 представлен случай поздней диагностики. Кривая 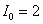на промежутке времени  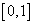соответствует стационарному состоянию с повышенным количеством входящего йода. Кривая  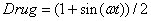соответствует варианту воздействия препаратами с переменной дозировкой, а кривая  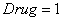соответствует варианту воздействия препаратами с постоянной дозировкой  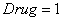на интервале 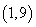. Кривая  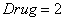соответствует варианту воздействия препаратами с постоянной дозировкой  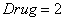на промежутке времени 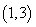. Расход препаратов в первом случае составил 5.6 единиц, во втором – 8 единиц, а в третьем – 4 единицы. Как в случае ранней, так и в случае поздней диагностики наименьшими являются расходы при переменной дозировке препарата. Полученные результаты по времени перехода после начала действия препаратов в нормальное функциональное состояние железы совпадают с результатами, полученными в [21, 22] – переход из возмущенного состояния в не возмущенное состояние происходит за 8 – 10 единиц времени, а количество поступающего в кровоток гормона и количество свободного в железе тиреоглобулина относятся как 4:1.

Заключение. Разработанная математическая модель функционирования щитовидной железы описывает основные биохимические реакции, протекающие в ней по синтезу гормона, и согласуется с экспериментальными данными клинических испытаний по выходным характеристикам. Математическое моделирование возможных нарушений функций железы и вариантов их лечения показало возможность планирования лечения с учетом необходимых экономических и временных ресурсов.

Литература:

1. Degon M., Chait Y., Hollot C. V., Chipkin S., Zoeller T. A Quantitative model of the human thyroid: development and observations // Proc. Amer. Control Conference, 2: 961–966.
2. Dietrich JW, Tesche A, Pickardt CR, Mitzdorf U. Thyrotropic Feedback Control: Evidence for an Additional Ultrashort Feedback Loop from Fractal Analysis. Cybernetics and Systems, 35: 315-331.
3. Leow M. K. S. A mathematical model of pituitary-thyroid interaction to provide an insight into the nature of the thyrotropin-thyroid hormone relationship. Journal of Theoretical Biology, 248 (2): 275–287.
4. Distefano J. J., Mak P. H. Optimal control policies for the prescription of thyroid hormones. Math. Biosci, 42: 159–186.
5. Degon M, Chipkin S. R., Hollot C. V., Zoeller R. T., Chait Y. A computational model of the human thyroid. Math. Biosci, 212 (1): 22–53.
6. Балыкина Ю.Е., Колпак Е.П. Математические модели функционирования фолликула щитовидной железы // Вест. С.-Петерб. ун-та. Сер. 10: Прикладная математика, информатика, процессы управления. – 2013. Вып. 3. С. 20 – 31.

7.      De Robertis E.D.P., Nowinski W.W., Caez F.A. Cell biology, 1970. Philadelphia – London – Toronto. W.B. Saunders Company, pp: 356.

8. Toda S., Aoki S., Suzuki K. et al. Thyrocytes, but not C cells, actively undergo growth and folliculogenesis at the periphery of thyroid tissue fragments in three-dimensional collagen gel culture. Cell and Tissue Research, 312 (3): 281-289.
9. Toda S., Koike N., Sugihara H. Thyrocyte integration, and thyroid folliculogenesis and tissue regeneration: perspective for thyroid tissue engineering. Pathology International, 51 (6): 403-417.
10. Danziger L., Elmergreen G.L. The thyroid-pituitary homeostatic mechanism. The bulletin of mathematical biophysics, 18 (1): 1–13.
11. Solomon A. Berson and Rosalyn S. Yalow. Quantitative Aspects of Iodine Metabolism. The Exchangeable Organic Iodine Pool, and the Rates of Thyroidal Secretion, Peripheral Degradation and Fecal Excretion of Endogenously Synthesized Organically Bound Iodine. J Clin. Invest., 33 (11): 1533–1552.
12. Gevertz J. L. Computational modeling of tumor response to vascular-targeting therapies part I: validation. Computational and Mathematical Methods in Medicine, 2011, Article ID 830515, 2011, 17 pages.
13. King A.C., Billingham J., Otto S.R., 2003. Differential equation. Linear. Nonlinear. Ordinary. Partial. Cambridg. University press, 541 p.
14. Hoermann R., Midgley J. E. M., Larisch R., Dietrich J. W. Is Pituitary Thyrotropin an Adequate Measure Of Thyroid Hormone-Controlled Homeostasis During Thyroxine Treatment? European Journal of Endocrinology. 168 (2): 271–280.
15. Hood A., Liu Y.P., GattoneV.H., Klassen C.D. Sensitivity oh thyroid gland growth to thyroid stimulating hormone (TSH) in rats treated with antithyroid drugs. Toxicological sciences, 1999, 49: 263-271.
16. Eisenberg M., Samuels M., DiStefano J. J. III. Extensions, validation, and clinical applications of a feedback control system simulator of the hypothalamo-pituitary-thyroid axis. Thyroid, 18 (10): 1071–1085.
17. Ebrahim N, R.M. Kershi R.M., Saif and B.N., RastrelliL. Physico-Chemical Analysis of Drinking Water from Maoh (Zafar) Village, Yemen. World Applied Sciences Journal 26 (2): 244-247.
18. Peper A. A theory of drug tolerance and dependence I: A conceptual analysis. Journal of Theoretical Biology, 229: 477–490.
19. Peper A. A theory of drug tolerance and dependence II: The mathematical model. Journal of Theoretical Biology, 229: 491–500.
20. Lüllmann H., Mohr K., Hein L. Taschenatlas Pharmakologie, 2008. Stuttgart; New York; Thieme: George Thieme Verlag, pp. 420.
21. McInerney D., Schnell S., Baker R. E., Maini P. K. A mathematical formulation for the cell cycle model in somitogenesis: analysis, parameter constraints and numerical solutions. Mathematical Medicine and Biology, 21: 85-113.
22. Riggs D. S. Quantitative aspects of iodine metabolism in man. Pharmacology Rev. 4 (3): 284.