This article examines statistics of hemodynamic studies. The author's model of forecasting of blood pressure values depending on the hemodynamic parameters.
Keywords: modeling, correlation coefficient, the method of least squares.
Любая наука, в том числе и физика, основывается на моделях. ![]() Обратимся к пониманию модели в работах А. М. Новикова и Д. А. Новикова, выделяя многочисленные черты понятия такие как: «любой образ, аналог, мысленный или условный посредством изображения, описания, схемы, чертежа, графика, плана, карты и т. п»., авторы дают и самое общее определение модели, как образ некоторой системы [4].
Обратимся к пониманию модели в работах А. М. Новикова и Д. А. Новикова, выделяя многочисленные черты понятия такие как: «любой образ, аналог, мысленный или условный посредством изображения, описания, схемы, чертежа, графика, плана, карты и т. п»., авторы дают и самое общее определение модели, как образ некоторой системы [4].
А. А. Леонтьев акцентирует внимание на том что, модель-это логическая (знаковая) конструкция, воспроизводящая те или иные характеристики исследуемого нами объекта при условии заранее определенных требований к соответствию этой конструкции объекту. Моделирование объекта — необходимый компонент его познания, но на нем это познание отнюдь не заканчивается [3].
Таким образом, обобщая вышеизложенное можно считать модель как материальный или мысленно представляемый объект, который в процессе изучения замещает объект, сохраняя некоторые важные для данного исследования черты. Или можно сказать другими словами:модель — это упрощенное представление о реальном объекте, процессе или явлении.
Модель необходима для того, чтобы:
‒ понять, как устроен конкретный объект и как он взаимодействует с другими объектами;
‒ прогнозировать процессы в случае изменения параметров, которые заложены в основу модели [1,2].
Любое исследование требует наличие умения ставить проблемы и задачи, прогнозировать результаты исследования, а значит, необходимо умение моделировать изучаемый процесс.
Приведем классификацию видов моделирования, которой можно описать физическое явление:
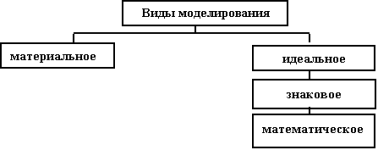
Рис. 1. Виды моделирования
Материальным (физическим)принято называть моделирование, при котором реальному объекту ставится в соответствие копия, в которую перенесены свойства рассматриваемого явления.
Идеальное моделирование — основано на мысленной аналогии.
Знаковое моделирование — это моделирование, использующее схемы, графики, чертежи.
Математическое моделирование — это моделирование, в котором объект описывается математическими формулами.
В физике рассматриваются множество моделей. В качестве примера можно привести модель материальной точки, модель идеального газа, модель атома и многие другие. Основная цель создания физической модели: в связи с очень сложными признаками и свойствами реального процесса, упростить его, чтобы описать явления. Физическое моделирование — первый этап рассмотрения и изучения знаний и средство проверки сформулированных гипотез в основе которой лежит выбранная модель. Физическая модель позволяет охватить явление или процесс во всем их многообразии, наиболее адекватна и точна, но менее универсальна [6,7]. При рассмотрении биофизических процессов организма человека, на сложные физические явления накладываются анатомо-физиологические и индивидуально-психологические факторы. В связи с этим в случае с биофизическими исследованиями мы предлагаем использовать именно математическое моделирование
На практике необходимо следовать определенному плану:
- Выделение явления, которое будут положено в основу модели и выделение предмета моделирования
- Рассмотрение свойств и процессов, влияющих на рассматриваемое явление
- Выяснение вопроса о влиянии свойств на рассматриваемое явление. В этом случае можно воспользоваться понятием коэффициента корреляции. Коэффициент корреляции — это безразмерная величина, которая показывает степень зависимости одной величины от другой.
- Для явления, которое в большей степени влияет на рассматриваемый процесс (коэффициент корреляции максимальный) построить математические формулы, по которым может изменяться процесс.
- Для проверки правильности выбранной формулы можно воспользоваться методом наименьших квадратов, согласно которому: чем меньше будет сумма квадратов отклонений эмпирических значений от теоретических значений, рассчитанных по соответствующим формулам, тем зависимость будет правильнее [5].
В качестве процесса, который мы положили в основу модели, рассмотрим формирование артериального давления. В качестве зависимых величин мы предлагаем рассмотреть следующие показатели: систолическое и диастолическое давление. В качестве независимых величин: ударный и минутный объем крови, рост, вес и возраст.
Для определения степени зависимости одних величин от других мы рассчитали коэффициенты корреляции и получили следующие значения
Таблица 1
Коэффициенты корреляции
|
|
Ударный объем крови |
Рост |
Вес |
Систолическое давление |
Диастолическое давление |
Возраст |
|
Минутный объем крови |
0,240 |
0,391 |
0,037 |
0,143 |
0,085 |
0,111 |
|
Ударный объем крови |
0,416 |
0,364 |
0,296 |
0,484 |
0,035 | |
|
Рост |
0,224 |
0,116 |
0,068 |
0,083 | ||
|
Вес |
0,001 |
0,207 |
0,245 | |||
|
Сист.д. |
0,657 |
0,052 | ||||
|
Диаст.д. |
0,263 |
Из таблицы 1 видно, что на величину диастолического давления больше всего влияет ударный объем крови (R= 0,484).
В качестве возможных моделей мы выбрали следующие зависимости: линейная, экспоненциальная, логарифмическая, степенная.
Для каждой из этих зависимостей можно построить математические формулы, которые представлены в таблице 2.
Таблица 2
Математические формулы для моделей
|
линейная |
ДИ=0,67Vуд+13,5 |
|
экспоненциальная |
ДИ=35,4e0,01Vуд |
|
логарифмическая |
ДИ=71,3ln(Vуд)-248 |
|
степенная |
ДИ=1,4* Vуд0,8691 |
Мы рассчитали суммы квадратов отклонений для выбранных функций, результаты которых представлены в таблице 3.
Таблица 3
Сумма квадратов отклонений
|
Вид функции |
Сумма квадратов отклонений |
|
линейная |
501,4 |
|
экспоненциальная |
507,5 |
|
логарифмическая |
495,2 |
|
степенная |
501,5 |
Сравнив суммы квадратов отклонений можно сделать вывод, что наиболее точной зависимостью является логарифмическая зависимость диастолического давления от ударного объема крови. Для данной зависимости нами была построена математическая формула: ДИ=71,3ln(Vу)-248.
Резюмируя вышеопределенные параметры нашего исследования, считаем возможным заключить, что никакая модель не может заменить само явление, но при решении задачи, когда нас интересуют определенное свойство изучаемого процесса или явления, модель оказывается полезным, а подчас и единственным инструментом исследования, познания.
Литература:
- Годфруа Ж. Что такое психология: В 2-х т. Изд. 2-е, стереотипное. Т.1.:Пер. с франц.- М.: Мир,1996.-496 с., ил. ISBN 5–03–001901–4
- Крутский А. Н. Психодидактика физики. Ч.4 Системно-функциональный подход к усвоению знаний.-Барнаул:БГПУ,1994.-143с.
- Леонтьев А. А. Основы психолингвистики.- М.: Смысл, 1997. — 287 с.
- Новиков А. М., Новиков Д. А. Методология научного исследования. — М.: Либроком. — 280 с.
- Орлов А. И. Прикладная статистика.-М.: Издательство «Экзамен», 2004. 656 с.
- Тулькибаева, Н. Н. Функции и содержание теста на определение уровня обученности, сформированности интеллектуальных способностей и типа мышления обучающегося / Н. Н. Тулькибаева. — Челябинск: Изд-во ЧГПИ,1993. -9с.
- Педагогическая энциклопедия: актуальные понятия современной педагогики / сост. Н. Н. Тулькибаева, Л. В. Трубайчук, О. Г. Учанова, З. М. Большакова и др.; под ред. Н. Н. Тулькибаевой, Л. В. Трубайчук. -М.: Издателский Дом «Восток», 2003.-273с.

