Поставлена математическая задача о двух взаимодействующих на отрезке популяциях по принципу хищник-жертва. Математическая модель представляет собой краевую задачу для системы двух нелинейных уравнений в частных производных. Исследуется устойчивость стационарных состояний. Для построения численного решения предлагаются методы, основанные на аппроксимации дифференциальных операторов. Теоретические результаты сопоставляются с результатами численных экспериментов.
Ключевые слова: популяция, краевые задачи, математическое моделирование.
Введение. Первые математические модели взаимодействующих популяций были предложены в работах Лотка и Вольтера в первой половине двадцатого века [12]. На сегодняшний день в математической популяционной биологии с учетом накопленных экспериментальных данных [9, 14, 16, 20, 24, 40, 41, 44, 48, 60-62, 67, 71, 81] разработаны различные модели с отличными от вольтеровских трофическими функциями, описывающими взаимодействие между популяции [1, 2, 4-7, 10, 13, 17, 23, 51, 63, 66, 68, 69, 75, 81]. Методы популяционной биологи, разрабатываемые изначально для решения задач о взаимодействующих популяциях как биологических объектов, стали успешно применяться и в других областях знаний – медицина [7, 23, 31], экономика [18, 19, 45, 46, 73, 74], социология [32, 77-79]. Значительная часть моделей в литературных источниках представлена задачей Коши для системы обыкновенных дифференциальных уравнений [1, 2, 4-6, 13, 81]. В таких моделях среда обитания считается гомогенной, плотность популяций не зависит от пространственных координат. Реальные среды обитания являются гетерогенными – свойства среды зависят от пространственных координат, соответственно от координат зависят и плотности популяций. Гетерогенность трофического ресурса и сформировавшиеся в эволюционном процессе стратегии выживания популяций вызывают у некоторой особей необходимость к расселению. При этом, как правило, особи перемещаются от мест с большей их численностью в места с меньшей их численностью. Математические модели в этом случае разрабатываются на основе аппарата уравнений в частных производных [8, 17, 23, 33, 35-39, 42, 58-60, 66-69, 81, 82].
Взаимодействующие популяции на отрезке. В качестве примеров линейных ареалов могут служить каналы, дороги, береговые линии озер и рек [9, 14, 20, 24, 41, 48, 61, 62, 67, 71, 81]. Математическая модель двух взаимодействующих на отрезке популяций для случая отрезка представляется системой двух эволюционных уравнений [6, 15, 17, 23, 38, 69, 81]
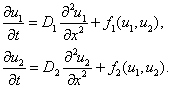 (1)
(1)
В этих уравнениях 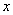 – координата,
– координата, 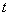 – время,
– время, 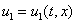 и
и 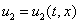 – линейные плотности популяций,
– линейные плотности популяций, 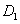 и
и 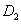 – параметры, характеризующие подвижности особей,
– параметры, характеризующие подвижности особей, 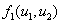 и
и 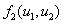 – трофические функции, характеризующие взаимодействие между популяциями.
– трофические функции, характеризующие взаимодействие между популяциями.
К системе уравнений (1) для случая отрезка длины 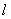 необходимо добавить начальные и граничные условия. В качестве начальных условий задается значение функций
необходимо добавить начальные и граничные условия. В качестве начальных условий задается значение функций 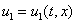 и
и 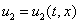 в начальный момент времени: при
в начальный момент времени: при 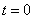
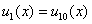 ,
, 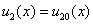 .
.
В качестве граничных условий рассматриваются два варианта:
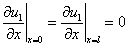 ,
, 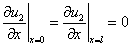 (2)
(2)
и
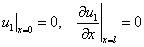 ,
, 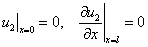 . (3)
. (3)
Условие обращения в ноль функций 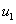 и
и 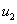 на границе отрезка соответствует невозможности существования популяции в этой точке, а условие обращения в ноль производных
на границе отрезка соответствует невозможности существования популяции в этой точке, а условие обращения в ноль производных 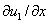 и
и 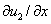 (условие наполнения среды [6, 60, 81]) допускает свободный рост численности популяций.
(условие наполнения среды [6, 60, 81]) допускает свободный рост численности популяций.
Общие численность первой и второй популяций (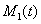 и
и 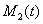 ) на отрезке в момент времени
) на отрезке в момент времени 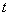 подсчитываются по формулам
подсчитываются по формулам
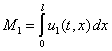 ,
, 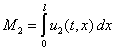 .
.
Для системы хищник-жертва (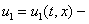 плотность жертвы,
плотность жертвы, 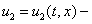 плотность хищника) функции
плотность хищника) функции 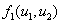 и
и 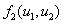 должны удовлетворять следующим условиям:
должны удовлетворять следующим условиям:
при 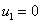 и
и 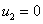 :
: 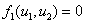 ,
, 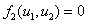 ,
, 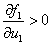 ;
;
при 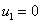 :
: 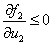 ,
, 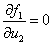 ; (4)
; (4)
при 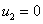 :
: 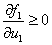 ,
, 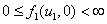 .
.
Первое условие означает, что популяции как жертвы, так и хищника в отсутствие особей на территории возникнуть не могут, второе – численность популяции хищника в отсутствие популяции жертвы как трофического ресурса хищника будет все время убывать. Третье условие соответствует началу зарождения популяции жертвы с не лимитированным ростом при малой ее численности на неограниченном трофическом ресурсе [6, 60, 81] (т.е. малочисленная популяция жертвы не погибает в отсутствие хищника).
В качестве моделей хищник-жертва ниже рассматриваются две модели с трофическими функциями [6] (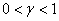 )
)
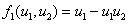 ,
, 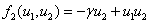 (5)
(5)
и
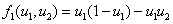 ,
, 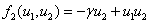 . (6)
. (6)
Первый вариант трофических функций соответствует модели Лотка-Вольтерра, во втором варианте учитывается внутривидовая конкуренция у жертвы [6].
Точечная модель следует из (1) при 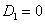 и
и 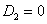
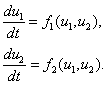 (7)
(7)
Стационарные точки этой системы уравнений находятся как решение системы алгебраических уравнений
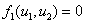 ,
, 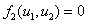 .
.
Устойчивость решений. Стационарные точки системы уравнений (7) (пусть 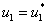 ,
, 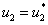 ) будут устойчивыми, если собственные значения матрицы Якоби
) будут устойчивыми, если собственные значения матрицы Якоби
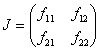 ,
,
где 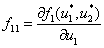 ,
, 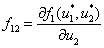 ,
, 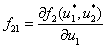 ,
, 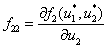 , в стационарных точках будут иметь отрицательные вещественные части. В нулевой стационарной точке с учетом условий (4), накладываемых на функции
, в стационарных точках будут иметь отрицательные вещественные части. В нулевой стационарной точке с учетом условий (4), накладываемых на функции 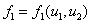 и
и 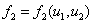 , одно собственное значение будет положительным и, соответственно, эта стационарная точка будет неустойчивой.
, одно собственное значение будет положительным и, соответственно, эта стационарная точка будет неустойчивой.
Стационарные решения системы уравнений (7) будут являться и решениями системы уравнений (1) при граничных условиях (2), если в качестве начальных условий принять 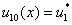 ,
,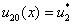 . Пусть наряду с этим решением существует близкое к нему решение
. Пусть наряду с этим решением существует близкое к нему решение
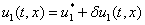 ,
, 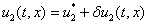
такое, что 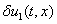 и
и 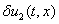 малые по сравнению с
малые по сравнению с 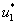 и
и 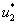 величины. Тогда с точностью до величин второго порядка малости из системы уравнений (1) следуют уравнения для
величины. Тогда с точностью до величин второго порядка малости из системы уравнений (1) следуют уравнения для 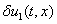 и
и 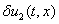
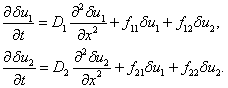 (8)
(8)
Решения этих линейных уравнений, удовлетворяющие граничным условиям (2), ищутся в виде тригонометрических рядов
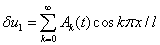 ,
, 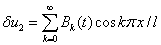 .
.
Коэффициенты 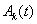 и
и 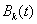 должны удовлетворять уравнениям (
должны удовлетворять уравнениям (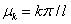 ,
, 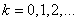 )
)
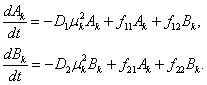 (9)
(9)
Решение этих уравнений будет устойчивым, если собственные значения матрицы Якоби
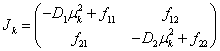 (10)
(10)
правой части этих уравнений будут иметь отрицательную вещественную часть для всех 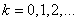 .
.
Для случая трофических функций (5) стационарная точка системы уравнений (7) 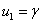 ,
, 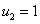 является центром, поскольку собственными значениями матрицы Якоби будут
является центром, поскольку собственными значениями матрицы Якоби будут 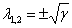 . Для случая системы уравнений (9) матрица Якоби (10)
. Для случая системы уравнений (9) матрица Якоби (10)
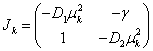
имеет собственные значения с отрицательной вещественной частью для всех 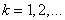 , а для
, а для 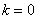 собственные значения совпадают с собственными значениями матрицы Якоби системы уравнений (7). Поэтому в окрестности этого положения равновесия
собственные значения совпадают с собственными значениями матрицы Якоби системы уравнений (7). Поэтому в окрестности этого положения равновесия 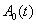 и
и 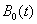 будут изменяться по гармоническому закону, а
будут изменяться по гармоническому закону, а 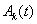 и
и 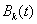 для
для 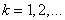 будут со временем стремиться к нулю. Соответственно общее решение системы уравнений со временем перестанет зависеть от пространственной координаты.
будут со временем стремиться к нулю. Соответственно общее решение системы уравнений со временем перестанет зависеть от пространственной координаты.
Для трофических функций (6) стационарной точкой уравнений (7) является 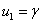 ,
, 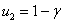 . Собственными значениями матрица Якоби в этой стационарной точке, поскольку выполняются неравенства
. Собственными значениями матрица Якоби в этой стационарной точке, поскольку выполняются неравенства 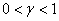 , будет пара комплексно сопряженных корней
, будет пара комплексно сопряженных корней 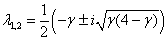 и, соответственно, стационарная точка является устойчивым фокусом.
и, соответственно, стационарная точка является устойчивым фокусом.
Собственные значения матрицы Якоби (10) системы уравнений (9)
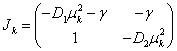
для всех  будут иметь отрицательные вещественные части. Поэтому при малых отклонениях от положения равновесия решение системы уравнения (8) будет стремиться к гомогенному решению
будут иметь отрицательные вещественные части. Поэтому при малых отклонениях от положения равновесия решение системы уравнения (8) будет стремиться к гомогенному решению  ,
, 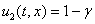 .
.
Для случая граничных условий (3) стационарной системе уравнений (1) удовлетворяет решение
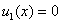 ,
, 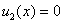 .
.
Решение уравнений для возмущений (8), удовлетворяющее граничным условиям (3), в окрестности этого стационарного решения представляется в виде тригонометрического ряда
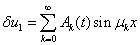 ,
, 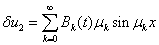
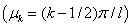 .
.
Матрица Якоби
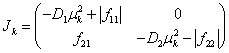
правой части уравнений (9) в силу условий (4), накладываемых на трофические функции, будет иметь собственные значения
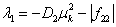 и
и 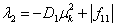 .
.
Первое собственное значение отрицательное, а второе будет отрицательным, для всех 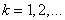 , если выполняется условие
, если выполняется условие 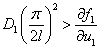 . При выполнении этого неравенства тривиальное решение будет устойчивым.
. При выполнении этого неравенства тривиальное решение будет устойчивым.
Численные методы решения. Построить аналитические решения нелинейной системы уравнений (1) не представляется возможным. Для их построения можно использовать различные численные методы. Основные из них – аппроксимация решения заданными аналитическими функциями, наилучшим образом удовлетворяющими исходным уравнениям [11, 21, 27, 29, 30, 47, 49, 50, 64, 65], аппроксимация дифференциальных операторов конечными разностями по пространственной и временной переменным с последующим решением систем нелинейных алгебраических уравнений [7, 15,17, 25, 38, 39, 43, 66-68] и аппроксимация дифференциальных операторов по пространственной переменной с последующим решением задачи Коши для системы нелинейных дифференциальных уравнений [22, 26, 28, 34, 52-57, 70, 72, 76, 80]. Для построения численного решения предлагаются три метода. Первый (вариационный) основан на представлении решения в виде отрезка тригонометрического ряда, второй – на дискретизации дифференциальных операторов по пространственной и временной переменным, третий – на сведении решения краевой задачи к задаче Коши для системы обыкновенных дифференциальных уравнений.
Вариационный метод. Решение системы уравнений (1) представляется в виде отрезка тригонометрического ряда
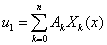 ,
, 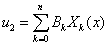 , (11)
, (11)
где 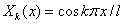 (
(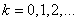 ) для граничных условий (2), и
) для граничных условий (2), и 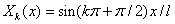 (
(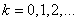 ) для граничных условий (3). В обоих случаях системы функций
) для граничных условий (3). В обоих случаях системы функций 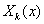 (
(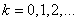 ) являются полными и ортогональными на отрезке
) являются полными и ортогональными на отрезке 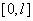 . После подстановки выражений (11) в уравнения (1), умножения последних на
. После подстановки выражений (11) в уравнения (1), умножения последних на 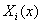 (
(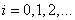 ) и последующего интегрирования по промежутку
) и последующего интегрирования по промежутку 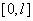 будет получена система обыкновенных дифференциальных уравнений для коэффициентов
будет получена система обыкновенных дифференциальных уравнений для коэффициентов 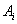 и
и 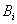 (
(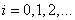 )
)
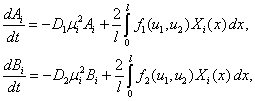 (12)
(12)
где 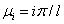 для граничных условий (2), и
для граничных условий (2), и 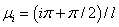 (
(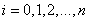 ) для граничных условий (3). Начальные условия для функций
) для граничных условий (3). Начальные условия для функций 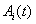 и
и 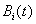 (
(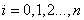 ) определяются из соотношений
) определяются из соотношений
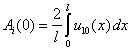 ,
, 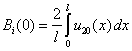 (
(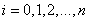 ).
).
Решение задачи Коши для уравнений (12) можно построить с применением различных численных методов [22, 26, 28, 34, 52-57, 70, 72, 76, 80], разработанных для интегрирования систем дифференциальных уравнений. В математическом пакете MatLab [35] для решения этой задачи можно использовать встроенную функцию ode45.
Метод сеток. Уравнения (1) аппрокисмируется конечными разностями на равномерной сетке по пространственной переменной с шагом 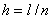 и с шагом
и с шагом 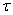 по временной переменной
по временной переменной
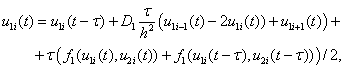
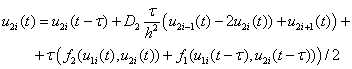 (13)
(13)
(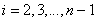 ),
),
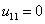 ,
, 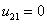 ,
, 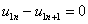 – для граничных условий (5)
– для граничных условий (5) 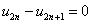 ,
,
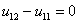 ,
, 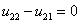 ,
, 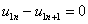 ,
, 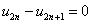 – для граничных условий (4).
– для граничных условий (4).
В начальный момент времени принимается 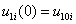 ,
, 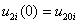 .
.
В (13) – 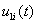 и
и 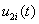 значение функций в
значение функций в 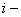 ом узле в момент времени
ом узле в момент времени 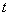 ,
, 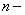 число отрезков, на которые разбивается интервал интегрирования
число отрезков, на которые разбивается интервал интегрирования 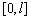 ,
, 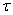 – шаг интегрирования по временной переменной.
– шаг интегрирования по временной переменной.
Метод редукции к задаче Коши. В этом методе осуществляется дискретизация уравнений (1) по пространственной переменной. Как и в методе сеток отрезок интегрирования 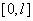 разбивается на
разбивается на 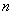 отрезков с узлами в точках
отрезков с узлами в точках 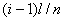 , в которых вводятся сеточные функции
, в которых вводятся сеточные функции 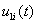 и
и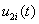 (
(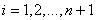 ). Для случая граничных условий (3) система уравнений (1) аппроксимируется системой обыкновенных дифференциальных уравнений (
). Для случая граничных условий (3) система уравнений (1) аппроксимируется системой обыкновенных дифференциальных уравнений (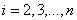 )
)
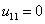 ,
,
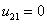 ,
,
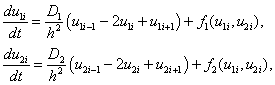
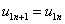 ,
,
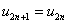
с начальными условиями (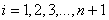 )
)
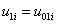 ,
, 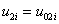 .
.
Решение этой задачи Коши можно строить с применением различных численных методов, модифицированных для решения систем дифференциальных уравнений большой размерности [22, 26, 28, 34, 52-57, 70, 72, 76, 80].
Как следует из анализа результатов численных экспериментов решение краевой задачи (1) – (2) для трофических функций (5) со временем независимо от выбора начальных условий становилось близким к гомогенному, для случая трофических функций (5) – к решению 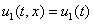 ,
, 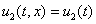 , описываемого системой уравнений (7), для функций (5) – к стационарному решению
, описываемого системой уравнений (7), для функций (5) – к стационарному решению 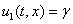
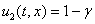 . Поэтому ниже приводятся основные результаты, полученные при решении уравнений (1) с граничными условиями (3) для трофической функции (6) с
. Поэтому ниже приводятся основные результаты, полученные при решении уравнений (1) с граничными условиями (3) для трофической функции (6) с 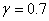 на отрезке единичной длины (
на отрезке единичной длины (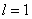 ,
, 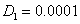 ,
, 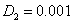 ). Численная реализация осуществлялась в среде программирования математического пакета MatLab [3, 35].
). Численная реализация осуществлялась в среде программирования математического пакета MatLab [3, 35].
В методе сеток система уравнений (11) на каждом временном шаге решалась с применением метода простой итерации [7, 17]. Сравнение результатов осуществлялось с решениями, полученными с использованием встроенных в MatLab функций. Результаты на сетках с 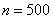 и
и 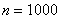 с шагом интегрирования
с шагом интегрирования 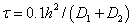 по временной переменной совпали с точность до 1%. Итерационный процесс сходился за 2 – 3 итерации при заданной степени точности (0.1%) для максимальных относительных отклонений во всех узлах сетки.
по временной переменной совпали с точность до 1%. Итерационный процесс сходился за 2 – 3 итерации при заданной степени точности (0.1%) для максимальных относительных отклонений во всех узлах сетки.
Решение уравнений (1) с граничными условиями (3) в вариационном методе аппроксимировалось отрезком ряда
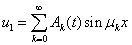 ,
, 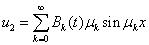
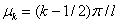 .
.
В качестве начальных условий принимались 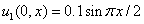 ,
, 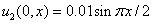 . Задача Коши для системы обыкновенных дифференциальных уравнений решалась с применением встроенной в MatLab функции ode45. Результаты численного интегрирования для случая 10 членов разложения представлены на рис. 1 – 4. На рис. 1 показано изменение значений коэффициентов
. Задача Коши для системы обыкновенных дифференциальных уравнений решалась с применением встроенной в MatLab функции ode45. Результаты численного интегрирования для случая 10 членов разложения представлены на рис. 1 – 4. На рис. 1 показано изменение значений коэффициентов 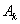
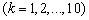 , а на рис. 2 –
, а на рис. 2 – 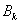
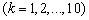 , в момент времени
, в момент времени 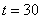 , в зависимости от номера
, в зависимости от номера 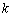 . На рис. 3 отображено изменение общей численности популяций (
. На рис. 3 отображено изменение общей численности популяций (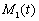 и
и 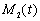 ) во времени и изменение коэффициентов
) во времени и изменение коэффициентов 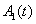 и
и 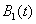 . Распределение популяций на отрезке в момент времени
. Распределение популяций на отрезке в момент времени 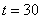 отображено на рис. 4 для вариационного метода, а на рис. 5 для метода сеток в моменты времени
отображено на рис. 4 для вариационного метода, а на рис. 5 для метода сеток в моменты времени 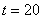 и
и 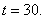
Все результаты, полученные с применением трех методов, совпали по изменению общей численности популяций во времени точностью до 1%. Времена решения уравнений с применением вариационного метода при 10 членах разложения, с применением метода сеток и метода редукции к задаче Коши на отрезке, разбитом на 100 интервалов интегрирования, практически не отличались.
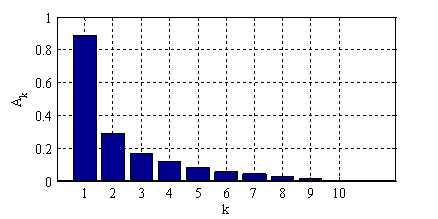
Рис. 1. Изменение коэффициентов  в зависимости от
в зависимости от 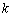 в момент времени
в момент времени 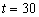
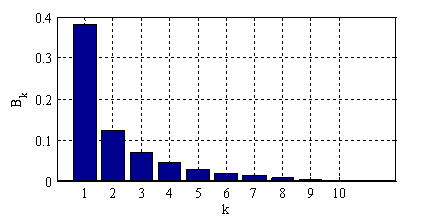
Рис. 2. Изменение коэффициентов 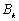 в зависимости от
в зависимости от 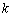 в момент времени
в момент времени 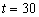
Рис. 3. Зависимость функций 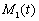 и
и  , коэффициентов
, коэффициентов  и
и  от времени
от времени
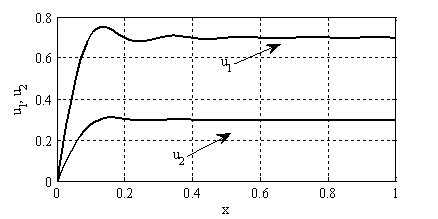
Рис. 4. Зависимость функций 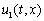 и
и 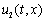 от координаты в момент времени
от координаты в момент времени 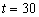
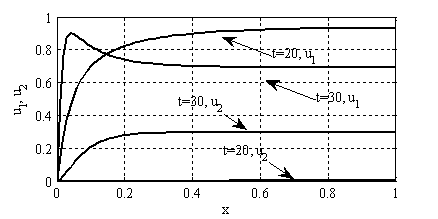
Рис. 5. Зависимость функций 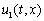 и
и 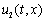 от координаты в момент времени
от координаты в момент времени 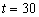 (метод сеток)
(метод сеток)
Заключение. Как следует из полученных выше результатов из «диффузионной» модели одиночной популяции следуют результаты, не содержащиеся в «точечных» моделях. Для популяции жертвы на отрезке с ограничениями роста на границах при высокой подвижности особей устойчивым может оказаться только тривиальное решение, если «подвижность» особей жертвы станет больше «критической».
Литература:
- Александров А. Ю., Платонов А.В Построение функций Ляпунова для одного класса систем нелинейных дифференциальных уравнений // Дифференциальные уравнения. – 2007. – Т. 43. – № 2. С. – 267-270.
- Александров А. Ю., Платонов А.В. Об абсолютной устойчивости одного класса нелинейных систем с переключениями // Автоматика и телемеханика. – 2008. – № 7. – С. 3-18.
- Андрамонов М. Ю., Тамасян Г. Ш. Реализация аналитического кодифференцирования в пакете matlab // Вычислительные методы и программирование: новые вычислительные технологии. – 2007. – Т. 8. – № 2. – С. 1-5.
- Апонин Ю. М., Апонина Е. А. Математическая модель сообщества хищник – жертва с нижним порогом численности жертвы // Компьютерные исследования и моделирование. – 2009. – Т. 1. – № 1. – С. 51-56.
- Апонин Ю. М., Апонина Е. А. Принцип инвариантности Ла-Салля и математические модели эволюции микробных популяций // Компьютерные исследования и моделирование. – 2011. – Т. 3. – № 2. – С. 177-190.
- Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий. – 2003. 368 с.
- Балыкина Ю. Е., Колпак Е. П Математические модели функционирования фолликула щитовидной железы // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. – 2013. – № 3. – С. 20-31.
- Баринов В. А., Перегудин С. И. Пространственные длинные волны в неоднородной жидкости над деформируемым дном // Вестник Тюменского государственного университета. – 2004. – № 4. – С. 250-256.
- Бигон М., Харпер Дж., Таунсенд К. Экология. Особи, популяции и сообщества: в двух томах. М.: Мир, 1989. Т. 1. 667 с. Т. 2. 477с.
- Будянский А. В., Цибулин В. Г. Моделирование пространственно-временной миграции близкородственных популяций // Компьютерные исследования и моделирование. – 2011. – Т. 3. – № 4. – С. 477-488.
- Буре В. М., Седунов Е. В. К вопросу об использовании интерполяционных кубатурных формул для вычисления коэффициентов Фурье // Известия высших учебных заведений. Математика. – 1981. – № 8. – С. 63-65.
- Вольтерра В. Математическая теория борьбы за существование. Москва-Ижевск:, Институт компьютерных технологий. – 2004. – 288 с.
- Гайко В. А. Глобальный бифуркационный анализ квартичной модели «хищник–жертва» // Компьютерные исследования и моделирование. – 2011. – Т. 3. – № 2. – С. 125-134
- Гилев А. В. Закономерности пространственного распределения и научные основы охраны рыжих лесных муравьев // Зоологический журнал. – 2010. – Т. 89. – № 12. С. – 1413-1420.
- Глызин С. Д. Разностная аппроксимация уравнения «реакция – диффузия» на отрезке // Моделирование и анализ информационных систем. – 2009. – Т. 16. – № 3. – С. 96-116.
- Горбач В. В., Кабанен Д. Н. Пространственная организованность популяции черного аполлона (parnassius mnemosyne) в условиях Заонежья // Зоологический журнал. – 2009. – Т. 88. – № 12. – С. 1493-1505.
- Горбунова Е. А., Колпак Е. П. Математические модели одиночной популяции // Вест. С.-Петерб. ун-та. Сер. 10. – 2012. – Вып. 4. – С. 18-30.
18. Гордеев Д. A., Малафеев О. А., Титова Н. Д. Стохастическая модель принятия решения о выводе на рынок инновационного продукта //Вестник гражданских инженеров. – 2011. – № 2. – С. 161-166.
19. Григорьева К. В., Иванов А. С., Малафеев О. А Статическая коалиционная модель инвестирования инновационных проектов // Экономическое возрождение России. – 2011. – № 4. – С. 90-98.
- Громов В. С. Пространственно-этологическая структура популяций грызунов. М.: Т-во научн. изданий КМК. – 2008. 581 с.
- Екимов А. В. Анализ множества достижимости нелинейных управляемых систем // Естественные и математические науки в современном мире. – 2014. – № 15. – С. 8-13.
- Еремин А. С., Олемской И. В. Вложенный метод интегрирования систем структурно разделенных обыкновенных дифференциальных уравнений // Журнал вычислительной математики и математической физики. – 2010. – Т. 50. – № 3. – С. 434-448
- Жукова И. В., Колпак Е. П Математическая модель солидной опухоли // Естественные и математические науки в современном мире. – 2013. – № 13. – С. 18-25.
- Зеленская Л. А. Численность и распределение птиц на острове Матыкиль (Ямские острова, Охотское море) // Зоологический журнал. – 2009. – Т. 88. – № 5. – С. 546-555
- Кабриц С. А. Мальков В. М., Мансурова С. Е. Математическое моделирование нелинейной деформации эластомерного слоя // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. – 2011. – № 3. – С. 56-63.
- Карелин В. В Один подход к задаче оценки параметров динамической системы в условиях неопределенности // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. – 2012. – № 4. – С. 31-36.
- Карелин В. В Точные штрафы в задаче наблюдения // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. – 2008. – № 4. – С. 3-8.
- Карелин В. В Точные штрафы в многоточечной задаче для обыкновенных дифференциальных уравнений // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. – 2009. – № 4. – С. 104-109.
- Карелин В. В. Точные штрафы в задаче оценки координат динамической системы в условиях неопределенности // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. – 2011. – № 4. – С. 40-46.
- Карелин В. В. Штрафные функции в задаче управления процессом наблюдения // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. – 2010. – № 4. – С. 109-114
- Колбин А. С., Хмельницкий О. К., Курылев А. А., Балыкина Ю. Е., Проскурин М. А., Колпак Е. П., Буре М. В. Первый в России опыт построения симуляционной модели исходов сахарного диабета 2-го типа с дискретным моделированием событий. клинико-экономическая экспертиза // Фармакоэкономика. Современная фармакоэкономика и фармакоэпидемиология. – 2013. – № 2. – С. 33-41.
- Колесин И.Д. Моделирование // Известия Российской академии наук. Теория и системы управления. – 2005. – № 2. – С. 75-80
- Колобов А. В., Полежаев А. А. Влияние случайной подвижности злокачественных клеток на устойчивость фронта опухоли // Компьютерные исследования и моделирование. – 2009. – Т. 1. – № 2. – С. 225-332.
- Колпак Е. П., Балыкина Ю. Е., Котина Е. Д., Жукова И. В. Математическая модель нарушений функционирования щитовидной железы // Молодой Ученый. – 2014. – № 2(61). – С. 19-24.
- Колпак Е. П. Mathlab: методы вычислений: учебное пособие / Е. П. Колпак; Санкт-Петербургский гос. ун-т. Санкт-Петербург. 2007.
- Колпак Е. П. Введение в механику сплошных сред учебное пособие / Е. П. Колпак; С.-Петерб. гос. ун-т. СПб. 2004.
- Колпак Е. П., Горбунова Е. А., Балыкина Ю. Е., Гасратова Н. А. Математическая модель одиночной популяции на билокальном ареале // Молодой ученый. – 2014. – № 1 (6). – С. 28-33.
- Колпак Е. П., Горбунова Е. А., Жукова И. В. Математическая модель популяционной волны // Естественные и математические науки в современном мире. – 2014. – № 16. – С. 25-41
- Колпак Е. П., Горбунова Е. А., Столбовая М. В., Балыкина Ю. Е Математическая модель логистической популяции на линейном ареале // Молодой ученый. – 2014. – № 3 (62). – С. 6-14.
- Колпак Е. П., Столбовая М. В. Математическая модель кинетики роста растений // Журнал научных публикаций аспирантов и докторантов. – 2013. – № 12 (90). – С. 230-232.
- Коробченко М. А. Расширение ареала крота европейского (talpa europaea) в долине реки Северный Донец // Зоологический журнал. – 2009. – Т. 88. – № 4. – С. 465-472.
- Котина Е. Д. К теории определения поля перемещений на основе уравнения переноса в дискретном случае // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. – 2010. – № 3. – С. 38-43.
- Котина Е. Д. О сходимости блочных итерационных методов // Известия Иркутского государственного университета. Серия: Математика. – 2012. – Т. 5. – № 3. – С. 41-55.
- Лидерман Г. В., Абатуров Б. Д., Быков А. В., Лопушков В. А. Динамика населения позвоночных животных Заволжской полупустыни. – М.: Наука, 2005. 252 с.
- Малафеев О. А., Пахар О. В. Динамическая нестационарная задача инвестирования проектов в условиях конкуренции // Проблемы механики и управления: Нелинейные динамические системы. – 2009. – № 41. – С. 103-108.
46. Малафеев О. А., Соснина В. В. Модель управления процессом кооперативного трехагентного взаимодействия // Проблемы механики и управления: Нелинейные динамические системы. – 2007. – № 39. – С. 131-144.
- Мальков В. М., Малькова Ю. В. Исследование нелинейной задачи Фламана // Известия Российской академии наук. Механика твердого тела. – 2006. – № 5. – С. 68-78.
- Мамонтов С. Н. Распределение по стволу дерева короеда-типографа (ips typographus, coleoptera, scolyniddae) и его энтомогафов // Зоологический журнал. – 2009. – Т. 88. – № 9. – С. 1139-1145.
- Матросов А. В. Вычислительная неустойчивость алгоритма метода начальных функций // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. – 2010. – № 4. – С. 30-39.
- Матросов А. В. Сходимость степенных рядов в методе начальных функций // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. – 2012. – № 1. – С. 41-51.
- Минкевич И. Г. Стехиометрия метаболических путей в динамике клеточных популяций // Компьютерные исследования и моделирование. – 2011. – Т. 3. – № 4. – С. 455-475.
- Олемской И. В Конструирование явных методов типа Рунге - Кутта интегрирования систем специального вида // Известия высших учебных заведений. Математика. – 2005. – № 2. – С. 75-80.
- Олемской И. В Структурный подход в задаче конструирования явных одношаговых методов // Журнал вычислительной математики и математической физики. – 2003. – Т. 43. – № 7. – С. 961-974.
- Олемской И. В. Вложенный пятиэтапный метод пятого порядка типа Дормана-Принса // Журнал вычислительной математики и математической физики. – 2005. – Т. 45. – № 7. – С. 1181-1191.
- Олемской И. В. Метод типа Рунге - Кутты интегрирования систем и дифференциальных уравнений второго порядка специального вида // Вычислительные технологии. – 2004. – Т. 9. – № 2. – С. 67-81.
- Олемской И. В. Четырехэтапный метод пятого порядка точности численного интегрирования систем специального вида // Журнал вычислительной математики и математической физики. – 2002. – Т. 42. – № 8. – С. 1179.
- Олемской И. В. Явный метод типа Рунге - Кутты пятого порядка // Вычислительные технологии. – 2005. – Т. 10. – № 2. – С. 87-105.
- Остроумов Е. Н., Котина Е. Д., Шмыров В. А., Слободяник В. В., Тонкошкурова В.В., Можейко Н. П., Ильинский И. М., Шумаков Д. В. Кардиоресинхронизирующая терапия и перфузия миокарда левого и правого желудочков // Вестник трансплантологии и искусственных органов. – 2012. – Т. XIV. – № 3. – С. 60-68.
- Перегудин С. И. Математическое моделирование физических процессов как компонент образования // Интеграция образования. – 2004. – № 3 (36). – С. 162-167.
- Ризниченко Г. Ю., Рубин А. Б. Биофизическая динамика продукционных процессов. Москва – Ижевск: Институт компьютерных технологий, 2004. – 464 с.
- Садыков О. Ф., Бененсон И. Е. Динамика численности мелких млекопитающих: Концепции, гипотезы, модели. – М.: Наука, 1992. 191 с.
- Сейфулина Р. Р. Аранеокомплекс (arachnida, aranei) в агросистемах кубанской равнины (видовой состав, пространственное размещение и сезонная динамика) // Зоологический журнал. – 2010. – Т. 89. – № 2. – С. 151-166.
- Стеряков А. А. Об одном универсальном методе построения моделей для сложных многоагентных систем // Компьютерные исследования и моделирование. – 2013. – Т. 5. – № 4. – С. 513-523.
- Тамасян Г.Ш Градиентные методы в вариационной задаче со свободными концами //Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. – 2012. – № 4. – С. 77-84.
- Тамасян Г. Ш Градиентные методы решения задачи коши // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. – 2009. – № 4. – С. 224-230.
- Тютюнов Ю. В. Пространственная модель развития устойчивости насекомых-вредителей к трансгенной инсектицидной сельскохозяйственной культуре // Биофизика. – 2007. – Т. 52. – № 1. – С. 95-113.
- Тютюнов Ю. В., Загребнева А. Д., Сурков Ф. А., Азовский А. И. Микромасштабная пятнистость распределения веслоногих рачков как результат трофически обусловленных миграций // Биофизика. – 2009. – Т. 54. – Вып. 3. – С. 508-514.
- Цыганов М. А., Бикташев В. Н. Солитонное и полусолитонное взаимодействие волн в возбудимых системах с нелинейной кросс-диффузией // Компьютерные исследования и моделирование. – 2009. – Т. 1. – № 1. – С. 109-115.
- Чеснокова О. И., Мелких А. В. Имитационное моделирование направленного движения в условиях градиента освещенности // Компьютерные исследования и моделирование. – 2012. – Т. 4. – № 2. – С. 401-406
- Шиманчук Д. В., Шмыров А. С Построение траектории возвращенияв окрестность коллинеарной точки либрации системы солнце–земля // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. – 2013. – № 2. – С. 75-84.
- Шиятов С. Г., Терентьев М. М., Фомин В. В., Циммерман Н. Е. Вертикальный и горизонтальный сдвиги верхней границы редколесий и сомкнутых лесов в XX столетии на полярном Урале // Экология. – 2007. – № 4. – С 243-248.
- Шмыров А. С., Шмыров В. А Cинтез оптимального управления орбитальным движением в окрестности коллинеарной точки либрации // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. – 2012. – № 4. – С. 139-146.
- Якушев В. П., Буре В. М., Якушев В. В. Методология и инструментарий анализа натурных данных в точном земледелии // Доклады Российской академии сельскохозяйственных наук. – 2008. – № 6. – С. 56-60.
- Якушев В. П., Буре В. М., Якушев В. В. Стохастическое моделирование в земледелии // Агрофизика. – 2011. – № 1. – С. 5-13.
- Aleksandrov A. Y., Platonov A. V., Kosov A. A. On the asymptotic stability of switched homogeneous systems // Systems & Control Letters. – 2012. – Т. 61. – № 1. – С. 127-133.
- Eremin A. S., Olemskoy I. V. An embedded method for integrating systems of structurally separated ordinary differential equations // Computational Mathematics and Mathematical Physics. – 2010. – Т. 50. – № 3. – С. 414-427.
- Kolesin I. D. Mathematical model of the development of an epidemic process with aerosol transmission // Biophysics. – 2007. – Т. 52. – № 1. – С. 92-94.
- Kolesin I. D. Self-organization and formation of small groups // Journal of Computer and Systems Sciences International. 2008. Т. 47. № 2. С. 252-259
- Kolesin I. D., Zhitkova E. M. Optimization of students' anti-epidemic prophylaxis // Automation and Remote Control. – 2008. – V. 69. – № 7. P. 1216-1222.
- Kotina E. D. Discrete optimization problem in beam dynamics // Nuclear Instruments and Methods in Physics Research. Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. – 2006. – Т. 558. – № 1. – С. 292-294.
- Murray D. D. Mathematical biology. N.Y. Springer. 2002. – 551 p.
- Peregudin S. I., Kholodova S. E. Specific features of propagation of unsteady waves in a rotating spherical layer of an ideal incompressible stratified electroconducting fluid in the equatorial latitude belt // Journal of Applied Mechanics and Technical Physics. – 2011. – Т. 52. – № 2. – С. 193-199.

