В данной работе проанализированы методы для численного решения обыкновенных дифференциальных уравнений, по итогам анализа была составлена программа, решающая задачу Коши. По результатам расчетов сделаны выводы о точности и ресурсозатратности рассматриваемых методов.
Ключевые слова: задача Коши, численные методы, обыкновенные дифференциальные уравнения.
Дифференциальные уравнения играют ключевую роль в математическом моделировании множества природных и технических процессов, включая механические колебания, динамику популяций, теплообмен и электрические цепи. Во многих случаях аналитическое решение таких уравнений невозможно или затруднительно, что делает численные методы основным инструментом их исследования.
Среди широко применяемых численных методов решения обыкновенных дифференциальных уравнений (ОДУ) можно выделить метод Эйлера, модифицированный метод Эйлера и метод Рунге-Кутта четвёртого порядка.
Метод Эйлера представляет собой один из наиболее простых численных методов решения начально-краевой задачи для обыкновенных дифференциальных уравнений (ОДУ) первого порядка. Он относится к одношаговым методам и основан на приближённом представлении решения с использованием разложения в ряд Тейлора первого порядка.
Рассмотрим обыкновенное дифференциальное уравнение первого порядка:
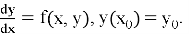
Метод Эйлера аппроксимирует искомую функцию последовательностью точек, вычисляемых по рекуррентной формуле:
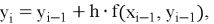
где
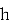
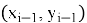
Геометрическая интерпретация метода заключается в замене неизвестного решения касательной, проведённой к кривой в точке
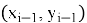
Локальная ошибка на каждом шаге выражается соотношением
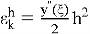
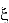
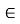
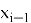
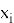
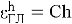
В методе Эйлера-Коши на каждом интервале расчет проводится в два этапа. На первом определяется приближенное решение на правом конце интервала по методу Эйлера, на втором уточняется значение решения на правом конце с использованием полу суммы тангенсов углов наклона на концах интервала. Уравнения для решения задачи (1) выглядят следующим образом:
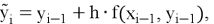
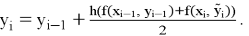
Данный метод имеет второй порядок точности. [2]
Все рассмотренные выше методы являются вариантами методов Рунге-Кутты. Остановимся на методе Рунге-Кутта четвертого порядка, так как он является одним из наиболее широко используемых численных методов решения обыкновенных дифференциальных уравнений, обеспечивает высокую точность приближённого решения без необходимости вычисления производных высших порядков.
Метод использует взвешенную сумму значений функции правой части в нескольких промежуточных точках для построения приближённого решения. Итерационная формула метода для решения (1) имеет следующий вид:
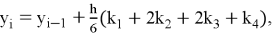
где
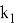
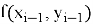
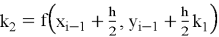
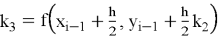
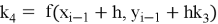
Каждый из коэффициентов
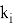
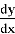
Данный метод обладает четвертым порядком точности, что означает, что его локальная погрешность составляет O(h 5 ), а глобальная — O(h 4 ). По сравнению с более простыми методами, такими как метод Эйлера или модифицированный метод Эйлера, он обеспечивает значительно более точное приближение при тех же значениях шага. Однако высокая вычислительная сложность метода (необходимость четырёх вычислений функции на каждом шаге) делает его менее эффективным для задач, где требуется высокая скорость расчётов. [1]
Разберем погрешность метода на конкретном примере. Необходимо решить следующую задачу:
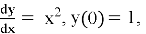
на интервале [0, 1] с шагом h = 0,1.
Аналитическое решение (6) выглядит следующим образом:
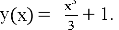
Согласно формулам (2)-(5) была составлена программа для решения (6) и вычислена погрешность, результаты расчетов представлены в таблице 1.
Таблица 1
|
Метод Эйлера |
Метод Эйлера-Коши |
Метод Р-К 4 порядка | ||||||
|
x |
y(x) |
Погрешность |
x |
y(x) |
Погрешность |
x |
y(x) |
Погрешность |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
0.1 |
1 |
-0.00033 |
0.1 |
1.0005 |
0.0002 |
0.1 |
1.00033 |
0 |
|
0.2 |
1.001 |
-0.00167 |
0.2 |
1.003 |
0.00033 |
0.2 |
1.00267 |
0 |
|
0.3 |
1.005 |
-0.004 |
0.3 |
1.0095 |
0.0005 |
0.3 |
1.009 |
0 |
|
0.4 |
1.014 |
-0.0073 |
0.4 |
1.022 |
0.0007 |
0.4 |
1.02133 |
0 |
|
0.5 |
1.03 |
-0.01167 |
0.5 |
1.0425 |
0,00083 |
0.5 |
1.04167 |
0 |
|
0.6 |
1.055 |
-0.017 |
0.6 |
1.073 |
0.001 |
0.6 |
1.072 |
0 |
|
0.7 |
1.091 |
-0.0233 |
0.7 |
1.1155 |
0.0012 |
0.7 |
1.11433 |
0 |
|
0.8 |
1.14 |
-0.03067 |
0.8 |
1.172 |
0.00133 |
0.8 |
1.17067 |
0 |
|
0.9 |
1.204 |
-0.039 |
0.9 |
1.2445 |
0.0015 |
0.9 |
1.243 |
0 |
|
1 |
1.285 |
-0.048 |
1 |
1.335 |
0.002 |
1 |
1.3333 |
0 |
|
Время, нс |
82193 |
Время, нс |
93154 |
Время, нс |
115134 | |||
Как видно из этой таблицы, самым точным является метод Рунге-Кутты, обеспечивающий нулевую погрешность при заданной точности 10– 4 . Метод Эйлера и его модифицированный аналог имеют накапливающуюся погрешность, однако стоит отметить, что они заметно быстрее и могут быть использованы для задач, где не так важна итоговая точность вычислений, либо количество вычислений невелико.
Литература:
- Зенков А. В. Численные методы: учебное пособие. — Екатеринбург: Изд-во Урал. ун-та, 2016. — 124 с.
- Коновалова Е. И. Численные методы математического анализа: учебное пособие — Самара: Издательство Самарского университета, 2022. — 149 с.: ил.

