О непараметрическом регуляторе для линейных динамических систем

Задача управления линейными динамическими системами является одной из наиболее распространенных на практике задач. При решении данной управления наиболее распространен параметрический подход, предполагающий, что при решении задачи идентификации мы заранее имеем представления об уравнении, описывающем объект. Обычно это означает, что мы должны знать, что система описывается дифференциальный уравнением, а также должны знать порядок этого дифференциального уравнения. Исходя из этой информации при известном входном воздействии рассчитываются коэффициенты данного уравнения, минимизирующие некоторый критерий (например, среднеквадратический критерий по выборке). Далее на основе имеющейся модели аналитически или численно рассчитывается закон оптимального управления (согласно тому или иному критерию), которое и подается на объект. На основе данного закона синтезируется регулятор способный решать поставленную задачу

Проблема данного подхода заключается в выборе порядка дифференциального уравнения. Дело в том, что априорные данные касательно этого имеются крайне редко, только для узкого класса хорошо изученных стандартных элементов. Из выборки же эти сведенья можно извлечь лишь строя всевозможные модели и сравнивая их на основе выбранного критерия, чтобы решить, какая лучше всего описывает систему. А это является довольно трудоемкой задачей.

В рамках данной работы предлагается принципиально другой подход к решению данной задачи, непараметрическая идентификация линейной динамической системой и непараметрическое управление ею. Непараметрическая теория, в отличие от предыдущей, предполагает, что известны только качественные характеристики системы, то есть только то, что система является линейной и динамической. Это означает, что использование непараметрической теории позволяет полностью уйти от неудобного вопроса выбора порядка дифференциального уравнения.

В качестве математической модели будем использовать описание системы через интеграл Дюамеля, т.е:

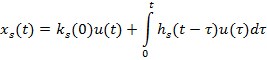
где k_s и h_s — оценки переходной и весовой функции соответственно.

Для оценки весовой функции необходимо на вход линейной динамической системы подать функция Хэвисайда:

В результате получается выборка {t_i, k_i}. В качестве оценки весовой функции будем использовать непараметрическую оценку регрессии Розенблатта — Парзена:

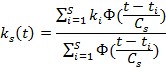
где S — объем выборки, C_S — коэффициент размытия, а Ф — колоколообразная функция.

Колоколообразная функция — функция удовлетворяющая следующим условиям:

1)     

2)     

Примерами функций удовлетворяющих данным соотношениям могут служить:

1)      Функция Гаусса:

2)      Параболическая функция:

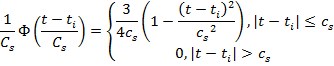
3)      Прямоугольная функция

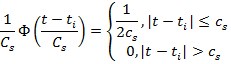
В случае, если измерения снимались через равномерные промежутки времени, то данную оценку можно упростить домножив числитель и знаменатель на . В этом случае, знаменатель превратится в оценку плотности случайной величины, а так как шаг изменения величины t — постоянный в оценку равномерного закона распределения. При условии что период наблюдения за объектом равен T получим:

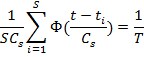
Отсюда получаем:

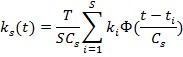
Переходная и весовая характеристики объекта связаны следующим соотношением:

Для того, чтобы построить оценку весовой характеристики продифференцируем оценку переходной характеристики:

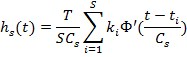
Подставив полученные соотношения в интеграл Дюамеля получим:

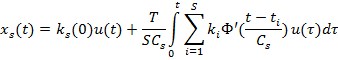
Для решения задачи управления поставим на вход исследуемой функции обратный данной системе оператор А^-1. При подаче на этот оператор желаемой траектории выход будет получен согласно схеме:

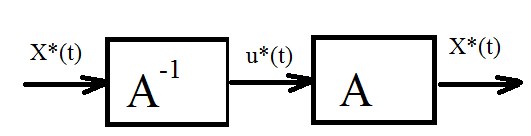
Рис. 1. Схема управления с непараметричесикм регулятором

Данный оператор так же будет линейной динамической системой с переходной и весовой характеристиками (будем называть их обратными) связанными с характеристиками исходной системы. На реальном объекте данные характеристики снять нельзя, так как для этого необходимо подавать ступеньку на выход объекта, что физически нереализуемо, однако их можно вычислить по модели. Это можно сделать исходя из следующих соображений:

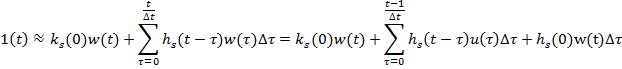
Отсюда:

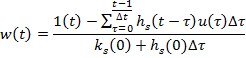
Таким образом мы можем получить выборку значений обратной весовой функции. В качестве значений прямой весовой функции могут служить как непосредственные измерения, так и непараметрические оценки.

Обратную весовую характеристику получим аналогично прямой т. е.:

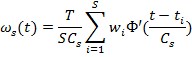
Таким образом, управление можно рассчитать по формуле:

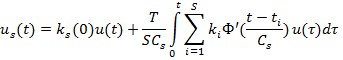
Регулятор, полученный таким образом, будем называть непараметрическим регулятором.

Для примера приведем результаты численного исследования для одного объекта. Уравнение, описывающее объект:

Выборка строилась на основе 100 точек взятых с шагом 0.1. Период наблюдения — 10 секунд. Выбирался оптимальный для решения задачи идентификации.

Переходная характеристика полученная аналитически:

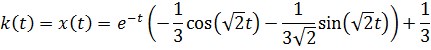
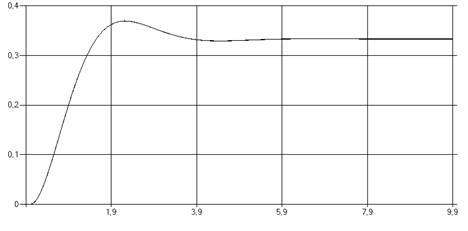
Рис. 2 Аналитически полученная переходная характеристика.

Непараметрическая оценка

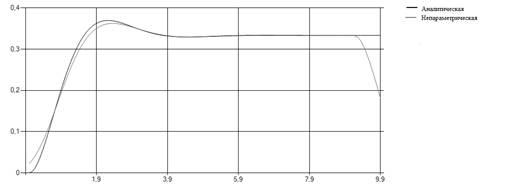
Рис. 3. Непараметрическая оценка переходной характеристики.

Резкое уменьшение значения непараметрической оценки на конце интервала связано со свойствами колоколообразной функции. Это можно преодолеть, либо наблюдая за объектом дольше, чем необходимо, либо, зная что в данном случае на конце интервала выход равен константе, искусственно прировняв выход модели этой константе на конце интервала. С учетом этой поправки построим непараметрическую модель объекта:

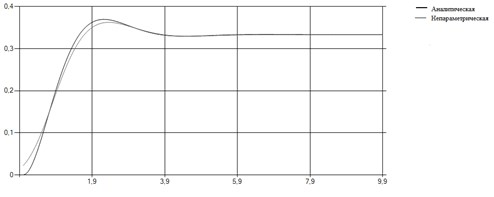
Рис. 4. Исправленная непараметрическая оценка переходной характеристики.

Посчитаем производную от переходной характеристики тем самым найдя ее аналитический вид и непараметирически оценим ее.

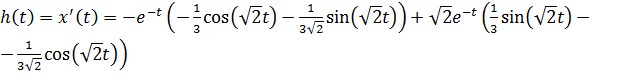
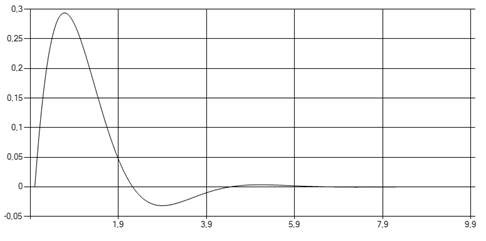
Рис. 5 Аналитически найденная весовая характеристика.

Непараметрическая модель весовой функции:

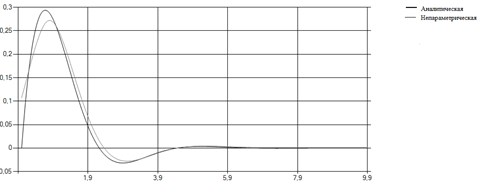
Рис. 6. Непараметрически найденная весовая характеристика.

Аналитическое предсказание реакции системы на входное воздействие u(t)=sin(t) есть решение диф. уравнения:

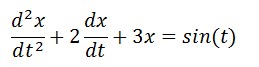
имеет аналитический вид: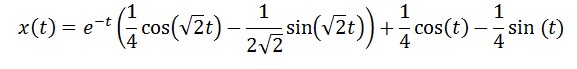

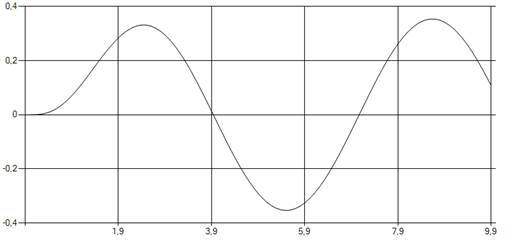
Рис. 7. Аналитическое предсказание выхода объекта при входе u(t)=sin(t).

Непараметрическая модель в данном случае показывает следующий результат

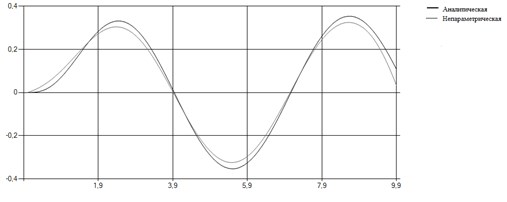
Рис. 8. Непараметрическое предсказание выхода объекта при входе u(t)=sin(t).

Характеристики непараметрического регулятора, т. е. обратная весовая и обратная переходная характеристики будут иметь следующий вид:

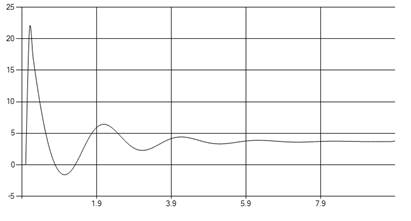
Рис. 9. Обратная переходная характеристика.

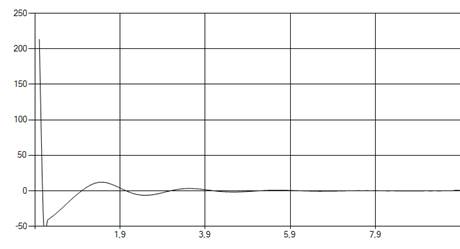
Рис. 10. Обратная весовая характеристика.

Проверим результат работы данного регулятора подав на вход объекта различные воздействия, в частности ступенчатое воздействие:

где div — оператор целочисленного деления (с отбрасыванием остатка), и синус.

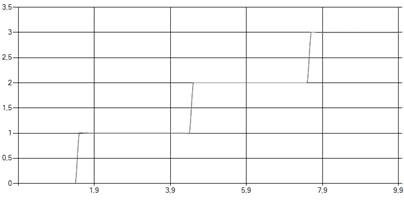
Рис. 11. Задание для ступенчатого воздействия

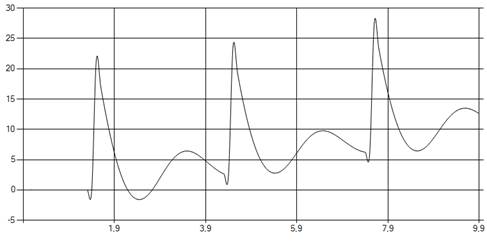
Рис. 12. Управление для ступенчатого воздействия.

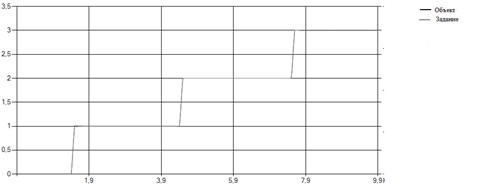
Рис. 13. Результат управления

Проведем аналогичный эксперимент с заданием вида u(t)=sin(x).

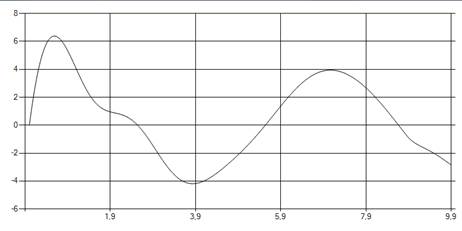
Рис. 14. Управление

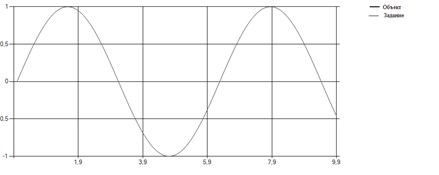
Рис. 15. Результат управления

Из вышеизложенного следует, что в идеальном случае, т. е. при отсутствии помех и ограничений на управление, непараметрический регулятор дает идеальное решение — траектория динамической системы полностью совпадает с желаемой траекторией.

Литература:

1.         Medvedev A. V. Identification and control for linear dynamic systems of unknown order. // Optimization Techniques IFIP Technical Conference / Berlin — Heidelderg — New-York: Springer — Verlag, 1975. — СC. 48–55.

2.         Медведев, А. В. Непараметрические системы адаптации / А. В. Медведев. Новосибирск: Наука. 1983.

3.         Агафонов Е. Д., Шестернева О. В. Математическое моделирование линейных динамических систем: учеб. пособие / Е. Д. Агафонов, О. В. Шестернева; Сиб. гос. аэрокосмич. ун-т. — Красноярск, 2010. — 92 с.