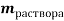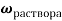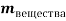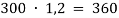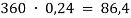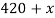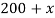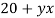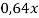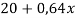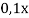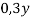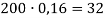В статье рассматриваются табличные методы решения задач на вычисление массовой доли растворённого вещества.

Ключевые слова: химия, табличный метод, массовая доля вещества.

Решение любых задач вызывают у обучающихся затруднения. Хотя решение задач — является одним из самых эффективных способов обучения: развивает навыки контроля и самоконтроля, помогает определить степень усвоение знаний и умений их использование на практике, позволяет выявлять пробелы в знаниях и умениях обучающихся и разрабатывать тактику их устранения. Самостоятельно справиться с решением задач могут немногие. Все больше и больше появляется задачи, имеющие практическое значение, которые являются также хорошим средством развития мышления учащихся. Поэтому на сегодняшний день тема решений таких задач является актуальной.

В данной статье я привожу метод решения химических задач на вычисления массовой доли растворенного вещества табличным способом. Данный способ не является новым, но в химии при решении задач редко используется. Сам метод очень удобный.

По сложности условно можно разделить эти задачи на:

I. Растворы, где меняется количество растворителя

II. Расчеты для одного раствора

III. Растворы, где меняется количество вещества

IV. Растворы, где меняется и количество вещества, и масса растворителя

V. Смешивание растворов.

Основные формулы, которые используются при решении задач:

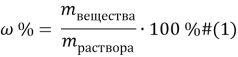
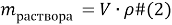
Рассмотрим примеры решения некоторых задач.

I . Растворы, где меняется количество растворителя

Задача № 1

К 300 мл 24 % раствора соли ( ) добавили 40 г воды. Вычислите массовую долю соли в полученном растворе.

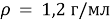
Дано:

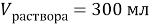
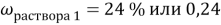
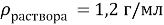
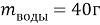
Найти:

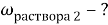
Занесем данные по условию задачи в таблицу 1 и произведем расчет возможных величин, помня, что числа в горизонтальных строчках можно умножать, а числа в вертикальных столбцах можно складывать (если добавляем, разбавляем) или вычитать (если упариваем). Нельзя складывать только массовую долю растворенного вещества между собой. Как правило за « x » — обозначаем то значение, которое необходимо найти.

Таблица 1

В последней строчке получаем линейное уравнение с одним неизвестным, решив которое мы получим ответ нашей задачи.

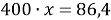
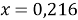
Ответ: 21,6 %

Задача № 2

Вычислите массу воды, которую нужно прилить к 420 г 15 % раствора соли, чтобы получить 9 % раствор.

Дано:

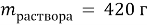
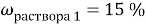
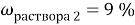
Найти:

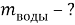
Таблица 2

По аналогии с предыдущей задачей в последней строчке получаем линейное уравнение с одним неизвестным, решив которое мы получим ответ нашей задачи.

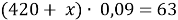
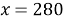
Ответ: 280 г

III . Растворы, где меняется количество вещества

Задача№ 3

Вычислите массу , которую необходимо растворить в 200 г раствора с массовой долей 10 %,чтобы получить 15 % раствор.

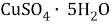
Дано:

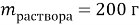
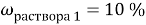
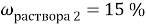
Найти:

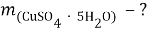
В этой задачи нам понадобится расчет малярных масс и . Рассчитаем молярную массу указанных веществ, используя периодическую таблицу Д. И. Менделеева:

;

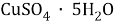
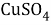
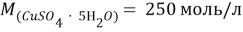
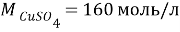
Таблица 3

В данной задачи мы сталкиваемся с кристаллогидратом. Необходимо произвести расчет массовой доли в кристаллогидрате:

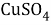
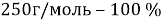
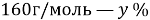
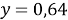
Полученное значение занесём в таблицу 3 и получим:

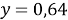
Таблица 4

Составим линейное уравнение:

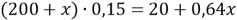
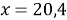
Ответ: 20,4 г

V . Смешивание растворов

Задача № 4

При смешивании 10 % и 30 % раствора соли получили 200 г 16 % раствора соли. Сколько граммов каждого раствора взяли?

Дано:

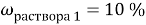
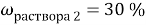
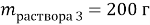
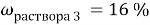
В этой задачи два неизвестных, поэтому вводим две переменные.

Таблица 5

Составим систему уравнению c двумя неизвестными:

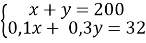
Ответ: ;

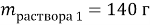
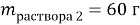
Анализ эффективности данного метода показывает, что процент решения задач этим методом намного выше чем привычным «методом стаканчиков». Задачи, где может применяться этот методом присутствуют на ЕГЭ и ОГЭ как по химии, так и по математики, что расширяет область его применения.

Литература:

1. Кузьменко Н. Е., Еремин В. В., Сборник Задач по химии с решениями / Н. Е. Кузьменко, В. В. Еремин –Москва: ООО «Издательский дом «ОНИКС 21 век»: ООО Издательство «Мир и Образование», 2003. — 640 с.
2. Кузьменко Н. Е., Еремин В. В., Попков В. А., Начала химии. Современный курс для поступающих в вузы (в 2 т.) / Н. Е. Кузьменко, В. В. Еремин, В. А. Попков — Москва: Экзамен: Издательский дом «ОНИКС 21 век», 2017.-448 с
3. Мацокина Г. Ф., Пособие по химии: методы решения расчетных и экспериментальных задач, Нижний Новгород 2015
4. Врублевский А. И., Задачи по химии с примерами решений, Минск: «Издательство Юнипресс», 2015.
5. Денисов В. Г., Выполнение заданий и решение задач повышенной сложности с комментариями и ответами для подготовки к единому государственному экзамену по химии (Алгоритмы выполнения заданий и способы решения задач) / В. Г. Денисов, Волгоград: Учитель, 2014.-133 с.