![]()
В данной работе делается попытка определения числа Рейнольдса и гидравлического сопротивления при двучленном законе фильтрации углеводородов в пористой среде с учетом влияния начального градиента, а также получена формула скорости в зависимости от этих параметров.
Ключевые слова: гидравлическое сопротивление, число Рейнольдса, двучленный закон фильтрации, начальный градиент.
In this paper, an attempt is made to determine the Reynolds number and hydraulic resistance with the two-term law of filtration of hydrocarbons in a porous medium, taking into account the influence of the initial gradient, and a velocity formula is obtained depending on these parameters.
Keywords: hydraulic resistance, Reynolds number, two-law filtration, initial gradient.
Как известно, из трубной гидравлики коэффициент гидравлического сопротивления ![]() является функцией числа
является функцией числа ![]() (1)
(1)
где Re — число Рейнолдса, ![]() — диаметр трубы,
— диаметр трубы, ![]() – средняя скорость движения жидкости,
– средняя скорость движения жидкости, ![]() — плотность жидкости,
— плотность жидкости, ![]() — вязкость жидкости.
— вязкость жидкости.
Используя формулу (1) и формулу Дарси-Вейсбаха ![]() , (2)
, (2)
где ![]() – перепад давления на длине трубы
– перепад давления на длине трубы ![]() . Фенчер, Льюис и Бернс [1] при исследовании явлений фильтрации воспользовались соотношениями трубной гидравлики, в которых скорость движения
. Фенчер, Льюис и Бернс [1] при исследовании явлений фильтрации воспользовались соотношениями трубной гидравлики, в которых скорость движения ![]() механически заменили скоростью фильтрации v, а диаметр трубы
механически заменили скоростью фильтрации v, а диаметр трубы ![]() заменили эффективным диаметром
заменили эффективным диаметром ![]() частиц, слагающих пористую среду. По полученным результатам на оси ординат отложены значения
частиц, слагающих пористую среду. По полученным результатам на оси ординат отложены значения ![]() на оси абсцисс — соответствующие им значения
на оси абсцисс — соответствующие им значения ![]() Полученные графики показали, что для чисел Рейнольдса меньше единицы прямолинейные участки кривых описываются уравнением
Полученные графики показали, что для чисел Рейнольдса меньше единицы прямолинейные участки кривых описываются уравнением
![]() (3)
(3)
где а — константа.
Уравнение (3) можно написать в виде
![]() , (4)
, (4)
т. е. получается закон Дарси.
При числах Рейнольдса больше единицы линейный закон нарушается.
Впервые гидродинамическое обоснование вопроса о границах применимости линейного закона фильтрации было произведено Н. Н. Павловским [2].
Он предложил формулу
![]() (5)
(5)
Павловский установил, что критическое значение числа Re колеблется в пределах ![]()
В. Н. Щелкачев [3] предложил выражение для числа Re в виде:
![]() . (6)
. (6)
где ![]()
Есть и другие авторы [4, 5, 6], предлагающие различные модификации формул для Re.
В предлагаемой статье определяется число Рейнольдса и гидравлическое сопротивление при двучленном законе фильтрации углеводородов в пористой среде с учетом влияния начального градиента.
Как известно, двучленный закон фильтрации углеводородов в пористой среде с учетом влияния начального градиента можно написать в виде:
![]() (7)
(7)
Если использовать формулу Дарси-Вейсбаха с учетом пористой среды, получаем:
![]()
![]() (8)
(8)
Сделаем подстановку
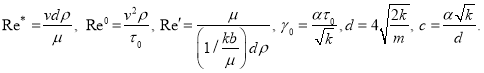 (9)
(9)
После несложных преобразований формула (8) принимает вид:
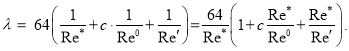 (10)
(10)
С другой стороны, формулу (7) представим в виде:
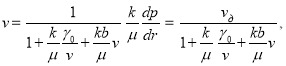 (11)
(11)
где ![]() – закон Дарси.
– закон Дарси.
Используя формулы (9) и подстановку ![]() получаем:
получаем:
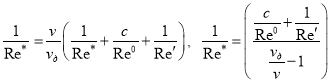 или
или
![]() (12)
(12)
Подставляя (12) в (10), получаем:
![]() . (13)
. (13)
Как видно из (13), если ![]() то получаем
то получаем ![]()
Таким образом, мы получили формулы для определения числа Рейнольдса, гидравлического сопротивления и скорости при двучленном законе фильтрации в зависимости от ![]() и
и ![]() с учетом начального градиента.
с учетом начального градиента.
Литература:
- Fancher G. H., Lewis J. A., Barnes K. B. Min/ Ind/Exp/ Sta/ Penn/ State College Bull., 12. 1933.
- Павловский Н. Н. Теория движения грунтовых вод под гидротехническими сооружениями и ее основные предложения. — Петроград, 1922.
- Щелкачев В. Н. Подземная гидравлика. –Ленинград, 1949.
- Мирзаджанзаде А. Х. и др. Гидравлика глинистых и цементных растворов. –Изд-во: Недра. — М., 1965.
- Маковей Н. Гидравлика бурения. –М.: Недра. –1986.
- Басниев К. С., Дмитриев Н. М., Каневская Р. Д., Максимов В. М. Подземная гидромеханика: Учебник для вузов. — М.-Ижевск: Институт компьютерных исследований, 2005. –496 с.

