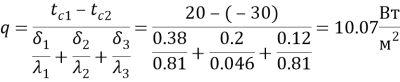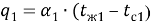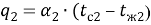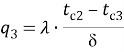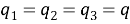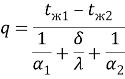В статье приводятся результаты расчётных исследований теплопроводности стенки аналитическим методом и методом конечных элементов в программе ANSYS. Также проанализированы сравнение расчётных методов теплопроводности.
Ключевые слова: теплопроводность, аналитический расчёт, МКЭ, ANSYS.
Введение
Теплопроводность представляет собой важное явление, определяющее способность материалов передавать тепловую энергию от области более высокой температуры к области более низкой температуры. Этот процесс осуществляется за счет хаотического движения частиц вещества, таких как атомы, молекулы и электроны. Понимание теплопроводности играет важную роль в науке о материалах, инженерии и технологических процессах.
Стационарные и нестационарные процессы теплопроводности в твердых телах представляют собой важные концепции. Стационарный процесс характеризуется постоянством параметров во времени и устанавливается при длительном поддержании температур на постоянном уровне. Напротив, нестационарный процесс представляет собой неустойчивый тепловой процесс, характеризующийся изменением температуры в пространстве и времени.
Ключевым показателем теплопроводности является коэффициент теплопроводности, который количественно характеризует способность материала проводить тепло. Он представляет собой количество теплоты, проходящее через единичный образец материала за единицу времени при единичной разнице температур. В системе СИ этот коэффициент измеряется в Вт/(м·K), что представляет собой количество тепловой энергии, переданное через единичный материальный образец при разнице температур в 1 К.
Исторически, передача тепловой энергии была объяснена концепцией перетекания гипотетического «теплорода» от одного тела к другому. С развитием молекулярно-кинетической теории, явление теплопроводности было более полно объяснено в контексте взаимодействия частиц вещества. Молекулы в областях с более высокой температурой движутся быстрее и передают свою энергию путем столкновений частицам в областях с более низкой температурой. Это взаимодействие частиц существенно влияет на тепловые свойства материалов и, следовательно, на их поведение в различных условиях.
В соответствии с [1, 2, 3] при разработке проектов зданий и сооружений необходимо строго соблюдать требования, представленные в соответствующих правилах, с целью обеспечения нескольких ключевых аспектов функционирования и эксплуатации. Эти требования включают в себя следующие аспекты:
Создание оптимальных условий микроклимата: Проектирование должно обеспечивать заданные параметры микроклимата внутри здания, необходимые как для комфорта людей, так и для эффективной работы технологического или бытового оборудования. Это включает в себя поддержание оптимальной температуры, влажности и циркуляции воздуха.
Тепловая защита: Ограждающие конструкции должны быть спроектированы с учетом эффективной тепловой защиты. Это важно для минимизации теплопотерь и обеспечения эффективности систем отопления и вентиляции.
Защита от переувлажнения: Проект должен предусматривать меры по защите ограждающих конструкций от избыточной влаги, которая может привести к различным проблемам, таким как гниение, плесень и коррозия.
Эффективное использование тепловой энергии: Проектирование должно стремиться к оптимальному расходу тепловой энергии на отопление и вентиляцию. Это включает в себя выбор эффективных материалов и систем теплоизоляции.
Надежность и долговечность конструкций: Важным аспектом является обеспечение долговечности ограждающих конструкций. Это достигается выбором материалов, обладающих необходимой стойкостью к внешним воздействиям, таким как мороз, влага, биологические воздействия, коррозия и другие разрушительные факторы окружающей среды. При необходимости следует предусмотреть специальную защиту элементов конструкций.
Такой комплексный подход к проектированию обеспечивает не только комфорт и безопасность внутри здания, но и его долговечность, что является важным аспектом устойчивости и эффективности любого строения.
1. Решение задачи теплопроводности через плоскую трёхслойную стенку при граничных условиях первого рода
На рисунке 1 показана принципиальная расчётная схема трехсловной стенки.
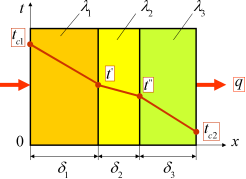
Рис. 1. Расчётная схема
Исходные данные для расчётов:
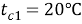
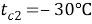
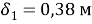
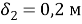
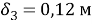
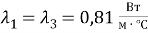
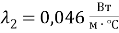
Удельный тепловой поток вычисляется по формуле 1.
|
|
(1) |
Таким образом аналитический расчёт показал, что удельный тепловой поток составляет 10,07 Вт/м 2 .
Результаты расчёта методом конечных элементов показаны на рис. 2 и 3.

Рис. 2. Распределение температуры
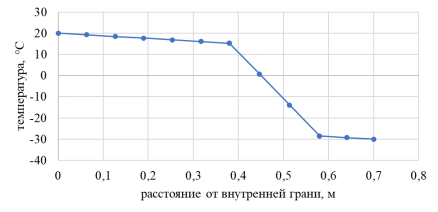
Рис. 3. График распределения температуры
Как видно из рисунков 2 и 3, в кирпичной кладке падение температуры достаточно медленное, утеплитель принимает на себя максимальный перепад температур.
Полученный тепловой поток, рассчитанный методом конечных элементов, составляет 10,069 Вт/м 2 .
Таким образом результаты расчёта аналитическим методом полностью совпадают с результатами расчёта методом конечных элементов.
2. Теплопроводность через плоскую однослойную стенку при граничных условиях третьего рода
На рисунке 4 показана принципиальная расчётная схема.
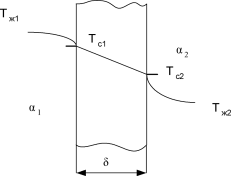
Рис. 4. Расчётная схема
Теплообмен на правой и левой поверхности стенки описывается законом Ньютона — Рихмана:
|
|
(2) |
|
|
(3) |
Теплообмен внутри стенки
|
|
(4) |
Так как теплообмен стационарный то
|
|
(4) |
Удельный тепловой поток вычисляется по формуле:
|
|
(5) |
Исходные данные для расчётов:
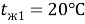
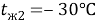
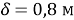
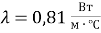
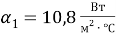
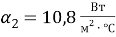
Удельный тепловой поток, определённой по формуле 5:
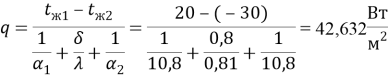
Температура внутренней стены:
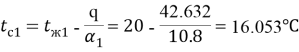
Температура наружной стены:
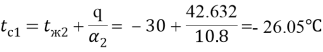
Результаты расчёта методом конечных элементов показаны на рисунках 5 и 6.

Рис. 5. Распределение температуры
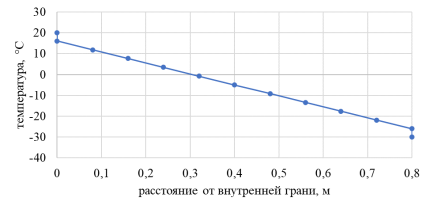
Рис. 6. График распределения температуры
Полученный тепловой поток, рассчитанный методом конечных элементов, составляет 42,632 Вт/м 2 .
Таким образом результаты расчёта аналитическим методом полностью совпадают с результатами расчёта методом конечных элементов.
Выводы
В ходе проведенных исследований было выявлено, что результаты решения задачи теплопроводности, полученные аналитическим методом и методом конечных элементов (МКЭ), полностью совпадают. Это подтверждает высокую точность и надежность МКЭ, что, в свою очередь, открывает перспективы для применения данного метода при решении более сложных задач теплопроводности, включая те, которые связаны с трехмерными моделями.
Было осуществлено детальное исследование распределения температур и величины теплового потока в задаче теплопроводности через плоскую трёхслойную стенку. При этом были использованы граничные условия первого рода, что предполагает непосредственное задание температуры на границах модели. Эти результаты не только позволили получить информацию о характере теплового процесса в материале, но и подтвердили применимость МКЭ для анализа подобных задач.
Дополнительно было проведено исследование распределения температур и величины теплового потока через однослойную стенку, используя граничные условия третьего рода. В данном случае на границах модели был задан тепловой поток. Полученные данные предоставляют более глубокое понимание процессов теплопроводности в таких условиях и подчеркивают гибкость МКЭ в обработке различных граничных условий.
Литература:
- СП 50.13330.2012 «Тепловая защита зданий». Актуализированная редакция СНиП 23–02–2003.
- ГОСТ 26253–2014 «Здания и сооружения. Метод определения теплоустойчивости ограждающих конструкций».
- СП 60.13330.2020 «Отопление, вентиляция и кондиционирование воздуха».