В статье авторы проводят анализ применимости уравнений Дубинина и Толмачева — Арановича для описания экспериментальных изотерм адсорбции в микропорах из банка данных по адсорбции, проводят расчёт и уточнение параметров этих уравнений.
Ключевые слова: изотермы адсорбции, адсорбция на микропорах, уравнение Дубинина, уравнение Толмачева — Арановича.
1. Изотермы адсорбции на микропорах
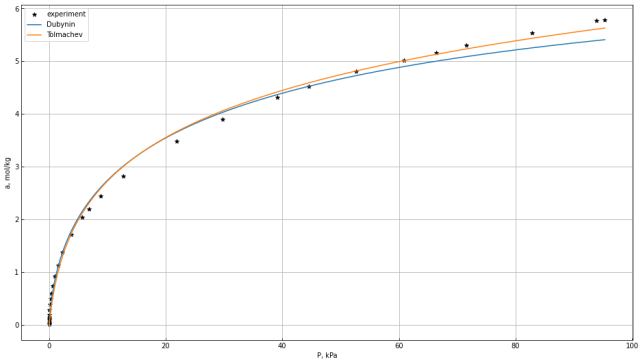
Рис. 1. Изотермы адсорбции на микропорах: Дубинина и Толмачева-Арановича
Адсорбция на микропорорах является наименее изученной из всех и требует для своего описания иных, чем на макропорах, уравнений. В настоящее время применяются различные эмпирические и полуэмпирические уравнения, а также современные тщательно проработанные термодинамические модели, главным образом решеточные.
Примером простой, но строго корректной термодинамически решеточной модели является модель японских ученых Оно и Кондо. [1]. В этой модели молекулы равных размеров и сферической формы и вакансии располагаются в узлах решетки. При этом учитываются их взаимодействия как с соседями по слою (горизонтальные взаимодействия, число таких взаимодействий Z г обычно принимается равным шести), так и с молекулами в соседних слоях (вертикальные взаимодействия, число таких взаимодействий Z в обычно принимается трем с каждым соседним слоем). Полное координационное число при этом Z равно двенадцати.
Особенности свойств адсорбционных систем и адсорбата в микропористых адсорбентах особенно заметно проявляются в поведении изотерм и изостер адсорбции, адсорбционной деформации адсорбента и термодинамических функций адсорбционных систем при изучении их в широких интервалах давлений и термодинамических функций адсорбционных систем при изучении их в широких интервалах давлений и температур. Например, в дифференциальные мольные изостерические теплоемкости адсорбционных систем проходят через максимум.
Линейность изостер адсорбции в области, где газы имеют значительные отклонения от идеальности, линейное их продолжение в области жидкого состояния адсорбтива и в закритической области — все это указывает на то, что адсорбат в микропористом адсорбенте — это особое состояние вещества [2].
Соответственно, в таком разительно отличном, от ситуаций на более крупных порах процессе необходимы свои уравнения.
Для описания адсорбции на микропористых адсорбентах используется полуэмпирическое уравнение Дубинина. n=2 для активных углей и n=3 для цеолитов.
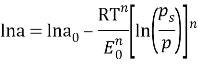
E 0 — характеристическая энергетическая величина сорбции стандартного пара (обычно бензол или азот).
Кроме того, также можно использовать уравнения, полученные из решеточных моделей.
Подставив написанные выше координационные числа в модели Оно-Кондо, а также приняв несущественные допущения при выкладках, можно получить [3] уравнение Толмачева-Арановича:
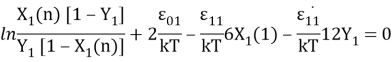
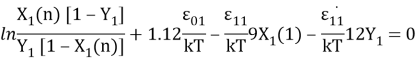
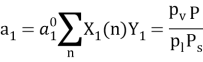
соответственно для одно- и двухслойной моделей.
Уравнения Дубинина, Толмачева-Арановича использовались нами в численном эксперименте.
2. Постановка практических задач
Существует множество банков данных по адсорбции, так, например, на базе Химического факультета МГУ собраны в сумме показатели более чем 2000 экспериментов, для многих из которых посчитаны константы для различных изотерм адсорбции [4]. Сами расчёты были проведены ранее программой в Excel’е, точность которой не отвечает современным требованиям. Кроме того, изотермы были рассчитаны не для всех экспериментов из банка данных, а также оставалось неизвестным, насколько хорошо приведенные уравнения описывают адсорбцию, и насколько одно лучше или хуже другого.
В связи с вышесказанным были поставленные следующие практические задачи:
1) Создать программный инструмент, позволяющий по ранее посчитанным параметрам строить графики по уравнений Дубинина и Толмачева-Арановича и сгладить экспериментальные кривые с помощью сплайна.
2) Научиться получать эти параметры регрессионными методами из экспериментальных данных и строить свои графики по уравнениям, не прибегая к заранее посчитанным параметрам, потому что они приведены не всегда и тем более не всегда являются самыми оптимальными.
3) Понять, насколько эти уравнения хорошо способны описать эксперимент, и какое из уравнение точнее описывает экспериментальные данные: Дубинина или Толмачева-Арановича.
Языком для написания программы стал Python, потому что в нем имеется модуль SciPy для научных вычислений, предоставляющий уже скомпилированные написанные на C/C++ функции для самых различных численных задач.
Визуализация посчитанного проводилась при помощи модуля matplotlib. Переводить медленно итерируемые списки чисел в шустро пробегаемые за счет статической типизации компилированного C-кода векторные массивы помогал модуль numpy. Открывались csv файлы функциями модуля Pandas.
Из самого SciPy использовались отдельные функции: для интерполяции Akima1DInterpolator как самый точный сплайн.
Векторные методы численного решения нелинейных уравнений scipy.optimize.root не дали должного результата, поэтому решение уравнения Толмачева-Арановича осуществлялось с помощью вручную написанной функции дихотомии.
Нахождение оптимальных параметров кривой осуществлялось с помощью функции scipy.optimize.curve_fit.
Написан класс Micro, включающий в себя метод инициализации по данным из файла, хранящий всю имеющуюся информацию оттуда и считающий по уравнениям значения адсорбции, а также находящий оптимальные параметры уравнения Толмачева-Арановича.
3. Ход работы
1) Считаны, отфильтрованы данные. Написаны функции уравнений Дубинина и Толмачева-Арановича (см. рис. 2)
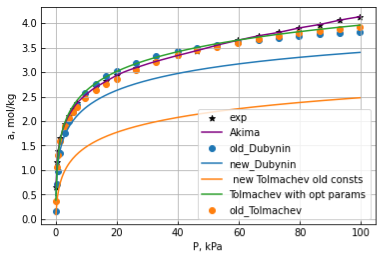
Рис. 2. Пример изотерм, посчитанных старой (old) и новой (new) программами
2) Опробованы 10 алгоритмов поиска корней библиотечной функции scipy.optimize.root. Ни один из них не дал удовлетворительных результатов для этого уравнения. Вручную написана и проверена функция поиска корня методом дихотомии (см. рис. 3)

Рис. 3. Код функции дихотомии
3) Произведена попытка воспроизвести изотерму Толмачева-Арановича для нескольких изотерм с уже посчитанными ранее параметрами. Она дала отрицательный результат: вид кривой — ломаная с большим горизонтальным участком .
4) Найдены оптимальные параметры уравнения Толмачева-Арановича, ипользуя функцию scipy.optimize.curve_fit.
5) Результат получился хорошим по точности,
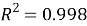
6) В этот момент оптимизация прошла снова успешно, однако получилось неадекватно большое значение предельной адсорбции, после чего он был ограничен и снова проведена оптимизация. Таким образом, оптимизируемыми параметрами остались только энергии взаимодействия адсорбат-адсорбент и адсорбат-адсорбати ограниченное значение максимальной адсорбции.
7) Получалась все так же «красивая» кривая, а коэффициент детерминации после ограничений снизился лишь незначительно и составил 0.9963. Это позволяет судить об устойчивости уравнения Толмачева-Арановича (см. рис. 4).
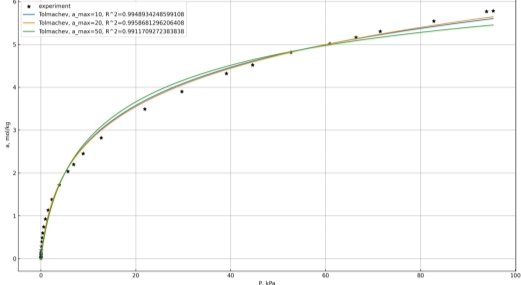
Рис. 4. Изотермы Толмачева-Арановича, полученные вариацией диапазона значений предельной адсорбции
8) Для масштабирования из 2530 изотерм каталога банка данных «Micro» отобрано 83 наиболее полных и качественных эксперимента
9) Получены графики для этих 83 файлов и результаты работы оптимизационного алгоритма. Результат оказался, в целом, положительным: для 47 из 83 экспериментов оптимальные параметры найдены успешно и соответствуют физическому смыслу задачи построения изотермы адсорбции. Средний коэффициент детерминации составил 0.9961 . Для остальных 36 успеха в оптимизации достигнуто не было предположительно из-за неправильного начального приближения.
Проанализированы старые значения для 83 штатно инициализирующихся файлов данных. В итоге средний по выборке
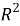
Обсуждение результатов
Метод «Dikhotomy», код которого приведен выше, написан вручную, а не реализован аналогичной функцией из библиотеки. Учитывая, что в уравнении Толмачева-Арановича искомый корень находится в интервале (0; 1), в качестве начального отрезка взят [1e-8; 1–1e-8]. Мы столкнулись с проблемой, что функция не всегда находила корень. Чтобы это исправить, были добавлены строчки 25–28, растягивающие отрезок втрое в случае отсутствия нулей функции на нем: + одна длина в каждую сторону. Необходимо заметить, что вне интервала (0; 1) под логарифмом получаются отрицательные значения, что не имеет физического смысла. Любопытно, что после этого, хотя логарифм попадал в недействительные значения, нахождение корней стало успешным.
В процессе работы пришлось столкнуться со следующими трудностями:
1) Низкое качество исходных данных. Из 2530 файлов 1970 так и не открылись, а на на местах чисел часто стояло «nan». Проблемы старой программы: посчитанные парметры уравнений Толмачева-Арановича, не воспроизводили кривую, посчитанную старой программой.
2) Вычислительная сложность оптимизационного алгоритма очень высока, и близко к крайним значениям мольной доли адсорбата возможно переполнение double в стеке функции в силу асимптотики логарифма. Также еще не найден наилучший способ выбора начальных приближений.
3) Учитывая, что подгоночный параметра в уравнени Дубинина один, а в уравнении Толмачева-Арановича их 3, сравнивать эти уравнения стоит в будущем проверить другие метрики для сравнения, кроме R 2
4) К настоящему моменту не анализировались, в этом же банке есть экспериментальные кривые, форма которых в принципе иная, и для которых предположительно оба эти уравнения будут подходить плохо.
Дальнейшие перспективы:
1) Найти способ выбора лучшего начального приближения и улучшить алгоритм оптимизации
2) Выполнить анализ на большей выборке и с большим количеством метрик.
Результаты и выводы
- Проведено сравнение уравнения Толмачева-Арановича со старыми и новыми оптимизированными параметрами с помощью с нуля написанной программы и уравнение Дубинина по их качеству описания экспериментальных данных через коэффициент детерминации.
- Замечены экспериментальные данные, в которых вид изотермы отличается от общего вида уравнений Дубинина и Толмачева-Арановича. Возможно, они не смогут быть описаны ни одним из использованных уравнений и может потребоваться другие уравнения.
- Уравнение Дубинина работает достаточно хорошо описывает экспериментальные данные адсорбции на микропорах, уравнение Толмачева-Арановича хуже со старыми, но лучше с новыми параметрами. Здесь предположительно дает значительный вклад большее число регрессионных параметров последнего уравнения. Успехом является избавление от отрицательных значений адсорбции и более высокий R 2 по сравнению со старыми точками из уравнения Толмачева-Арановича.
- Уравнение Толмачева-Арановича проверено на устойчивость к изменению допустимого диапазона параметров: оно оказалось неустойчивым. Такие константы, как давление насыщенного пара, предельное значение адсорбции могут меняться в десятки и сотни раз, сохраняя R^2 кривой выше 0.99. При этом относительно небольшие вариации энергий могут принципиально изменить вид графика.
Литература:
- Оно С., Кондо С. Молекулярная теория поверхностного натяжения в жидкостях Издательство ИЛ, 1963. — 290 с
- А. М. Толмачев, Термодинамика адсорбции газов, паров и растворов (Спецкурс).
- А. М. Толмачев, методическая разработка к курсу лекций по физической химии для 313–413 группы
- http://adsbank.chem.msu.ru/

