Изучение и использование алгоритма Л. Ф. Магницкого. При построении математической модели алгоритма Л. Ф. Магницкого возможно быстрое решение практических задач на смешивание веществ.
Ключевые слова: алгоритм, арифметика Магницкого, смеси, модель.
Studying and using L. F. Magnitsky's algorithm. By constructing a mathematical model of L. F. Magnitsky's algorithm it is possible to quickly solve practical problems on mixing substances.
Keywords: algorithm, Magnitsky's arithmetic, mixtures, model.
При решении практических задач из разных предметных областей появляется возможность не только лучше понять учебный материал других дисциплин, а также развить мышление и провести исследование в соответствии с поставленной целью. При этом первостепенное значение должно отводиться моделированию, так как модели могут имитировать существенные черты объектов-оригиналов и достаточно точно воспроизводить их поведение.
Создание математических моделей реальных процессов и явлений, а затем проведение эксперимента на математических моделях — одно из перспективнейших направлений использования прикладного математического аппарата при проведении исследовательской деятельности.
Технология математического моделирования лучше всего осваивается на задачах из разных предметных областей: математики, физики, химии, биологии, экономики и др. Предлагаем вашему вниманию задачу из области химии.
Как следует смешивать различные вещества, чтобы получать смеси определенной пробы, концентрации или цены?
С подобным вопросом люди сталкивались не только в старину — и в современном мире человеку зачастую приходится искать ответы на поставленный вопрос. Попытаемся ответить на него с помощью старинного алгоритма Л. Ф. Магницкого, работая по следующему плану:
1) изучить старинный алгоритм на смешивание веществ, предложенный Л. Ф. Магницким;
2) изобразить алгоритм в виде схемы;
3) решить задачи на смешивание двух веществ с помощью алгоритма Л. Ф. Магницкого;
4) провести анализ полученных результатов, найти практически значимые способы применения полученной «полезной модели».
Рассмотрим следующую задачу:
Пусть имеется серебро двух разных проб: одно — 11-й, а другое — 14-й пробы. Сколько какого серебра надо взять, чтобы получить 1 фунт серебра 12-й пробы?
Примечание. В России существовала золотниковая система обозначения пробы на основе русского фунта, содержащего 96 золотников. Проба выражалась весовым количеством благородного металла в 96 единицах сплава. Например, фраза «серебро 11-й пробы» означает, что в 96 единицах некоторого сплава содержится 11 частей серебра. В настоящее время проба означает число частей благородного металла в 1000 частях — по массе — сплава.
Решим данную задачу по алгоритму Л. Ф. Магницкого, предложенному им в его знаменитой книге «Арифметика» (1703 г) [1].
Алгоритм.
Для того, чтобы алгоритм Л. Ф. Магницкого был более понятен на современном языке, изобразим его в виде схемы:
1. Запишите друг под другом две исходные пробы имеющегося вещества (11; 14).
2. Слева от них и примерно посредине запишите пробу смеси (12).
3. Соедините написанные числа черточками. Получится такая схема (рис. 1):
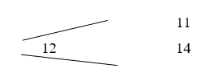
Рис. 1. Исходная математическая схема смесей
4.Меньшую пробу (11) вычтите из пробы смеси (12); полученный результат (1) запишите справа от большей пробы.
5. Из большей пробы (14) вычтите пробу смеси (12); результат (2) запишите справа от меньшей пробы. Схема примет следующий вид (рис. 2):
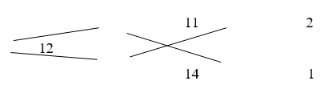
Рис. 2. Результирующая математическая схема смесей
Ответ. Таким образом исходя из алгоритма Л. Ф. Магницкого получаем: для получения 1 фунта серебра 12-й пробы нужно взять 2 части (0,67 фунта) серебра 11-й пробы и 1 часть (0,33 фунта) серебра 14-й пробы.
Построение математической модели на смешивание двух любых веществ
Обычно сначала строят математическую модель, а затем алгоритм. В данном случае алгоритм нам известен. По заданному алгоритму построим математическую модель. Однако прежде определим, что «дано» и что необходимо «найти» в нашей задаче [2] [3].
Дано: а— проба (или концентрация, или цена) 1-го вещества;
b — проба (или концентрация, или цена) 2-го вещества;
c — проба (или концентрация, или цена) смеси;
Ko l— вес (или объем) смеси в г (л, мл или фунтах и т. д.);
Sm — единицы измерения смеси (фунт, мл, л, г, кг и т. д.).
Найти:
rа — количество частей 1-го вещества для смешивания;
rb — количество частей 2-го вещества для смешивания;
rr — вес (или объем) 1-го вещества в смеси.
Связь:
rr =kol · ra/(ra + rb);
kol — rr — объем 2-го вещества в смеси.
При построении математической модели на смешивание двух любых веществ по алгоритму Л. Ф. Магницкого рассмотрим три случая:
а) при а < с
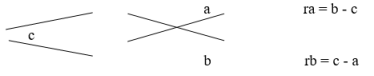
б) при а > с > b:
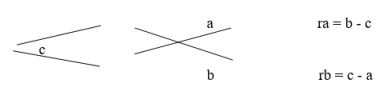
в) при а, b, с < 0 или (с > а и с > b): нет решений.
Два первых варианта а), б) имеют решение; изобразили его двумя схемами (при а < с <b; а="" при=""> с > b) и там же записали формулы для вычислений rа, rb. Для варианта в) нет решений (при а, b, с < 0 или (с > а и с > b)). </b;>
Представим решение данной задачи математическим методом:
Пусть х частей первого сплава нужно взять, а (1-x) частей — второго сплава. Тогда получим уравнение 11х+14(1-x) =12. Решим его:
11x+14–14x=12
—3x=-2
х=
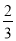
1-
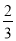
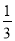
Отсюда следует, что первого сплава потребуется 2 части, а второго — 1 часть. Нетрудно подсчитать массы сплавов по их частям: 0,67 фунта первого сплава и 0,33 фунта второго.
Данный алгоритм обладает свойством массовости, то есть применим для определенного типа задач [4] [5] [6].
Проверим справедливость расчетов с помощью алгоритма при решении другой задачи:
На фабрике два сорта чая — по 40 и 60 рублей за кг. По сколько килограммов чая каждого сорта надо взять для получения 400 кг смеси по 55 руб. за 1 кг?
Решим эту задачу двумя способами: формально выполним расчеты с помощью алгоритма Магницкого (рис. 3).

Рис. 3. Математическая модель алгоритма Магницкого для решения задачи
Получили следующий результат: первого сорта чая потребуется 5 частей или по массе это 100 кг, а второго сорта — 15 частей, то есть по массе 300 кг.
Решим задачу математически:
Пусть х кг чая первого сорта надо взять, тогда (400-х) кг — чая второго сорта. 40х руб. — стоимость взятого чая первого сорта, 60(400-х) руб. — стоимость чая второго сорта. Смесь стоит 55*400 рублей. Получаем уравнение: 40х+60(400-х) =55*400. Решив его, получим х=100 — т. е. столько килограммов чая первого сорта взяли, 400–100=300 кг чая второго сорта взяли.
Полученная в работе «полезная модель» может иметь большое практическое значение, позволит получать смеси определенной пробы, концентрации или цены. Дальнейшее её развитие и целесообразность использования при проведении химических опытов, при составлении смесей разной природы с различным содержанием входящих компонентов и т. п. наглядно представит простоту, удобство и широту применения алгоритма Л. Ф. Магницкого [4] [5] [6].
Литература:
- Магницкий, Леонтий Филиппович Арифметика [Электронный ресурс] // Математическая библиотека. URL: http://math.ru/lib/176 (дата обращения 15.04.2022).
- Математические этюды [Электронный ресурс] // URL: http://www.etudes.ru/ (дата обращения 10.04.2022).
- Олесник, С. Н. Старинные занимательные задачи: / С. Н. Олесник, Ю. В. Нестеренко, М. К. Потапов. — М.: 1985. — 224 с, ил.
- Макарова, Н. В. Системно-информационная концепция курса школьной информатики / Н. В. Макарова // Информатика и образование. — 2002 — № 8 — с. 17–19.
- Сандалова, С. Я. Линейные, разветвляющиеся и циклические алгоритмы: / С. Я. Сандалова. — Хабаровск: ЛИТ, 2003. — 278 с.
- Газизова Н. Н., Зиннурова О. В., Фаттахов Д. А. Построение математической модели смешения веществ // Современные решения научных и производственных проблем в химии и нефтехимии. — 2021, — c.341–351.

