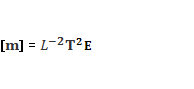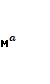Использование алгоритма анализа размерностей физических величин в школе (механика)

В настоящее время анализ размерностей физических величин и теория подобия физических явлений (далее АР) широко используются при решении задач в физике и её технических приложениях [1, 2]. В учебниках технических дисциплин высшей школы анализу размерностей и теории подобия физических явлений отведено определённое место.

Использование АР в средней школе сводится к проверке равенства размерностей выражений, входящих в левую и правую части итоговых формул, полученных при решении задач физики. Такую форму использования АР можно назвать «первым уровнем использования АР». В большинстве школьных пособий по физике использование такой формы АР рекомендовано авторами.

В данной работе предлагается доступный школьникам «второй уровень использования АР», названный универсальным алгоритмом анализа размерностей, позволяющий выявлять искомую итоговую формулу с точностью до безразмерного множителя.

Рассмотрим его на примере решения задачи механики № М1.

I. Универсальный алгоритм анализа размерностей

Задача № М1. Вычислить первую космическую скорость для Земли.

Решение

Основой анализа размерностей служит следующее суждение: «Размерности обеих частей любого уравнения физики должны быть одинаковы».

Процесс решения задачи разобьем на 9 этапов.

1 этап. Схематизация явления, выбор расчётной схемы, допущение о перечне управляющих параметров явления

1. Схематизация явления, выбор расчётной схемы

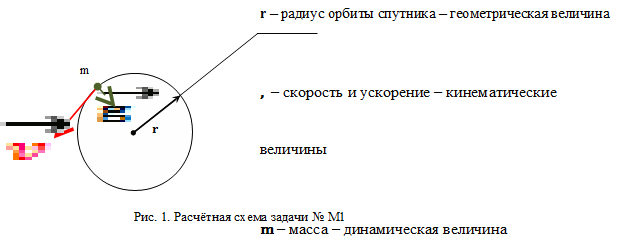
Необходимо сделать рисунок и указать на нём все заданные и искомые величины. Это и есть расчётная схема явления, отражённого физической задачей – см. рисунок 1. Её также можно назвать и расчётной схемой задачи.

1. Допущение о перечне управляющих параметров

Пусть первая космическая скорость будет управляемым параметром.

Предположим, что она может зависеть от следующих управляющих параметров:

1. Радиуса траектории спутника;

2. Ускорения свободного падения на уровне круговой орбиты спутника;

3. Массы спутника.

§

Этап 1 очень важный (особенно для научных задач). Он завершается формулировкой задачи в обобщённой форме.

Формулировка задачи в обобщённой форме

Установить связь между величинами .

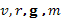Дано:

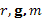
(1)

Найти:

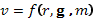
Запись (1) отражает формулировку задачи в обобщённой форме.

Примечания к этапу 1

А. Рисунок (расчётная схема задачи) отражает и постановку задачи, и, частично, – решение задачи.

Б. Искомую величину будем называть управляемым параметром. А заданные величины – управляющими параметрами.

В. Все параметры являются равноправными физическими величинами. Выбор управляемого параметра в известной степени произволен. Существенным является то, чтобы перечень всех параметров задачи был полным.

Г. Полноту перечня всех параметров не всегда удаётся выявить заранее. Часто она выявляется в процессе решения задачи (в том числе путём перебора различных вариантов перечня).

Д. На этапе 1 большое значение имеет физическая интуиция исследователя (в данном случае, учащегося, решающего учебную задачу).

2 этап. Предположим, что функция – степенная

Какой может быть функция ?

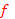Предположим, что функция 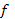– степенная.

Т. е.

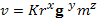, (2)

где

[ ] – размерность физической величины, указанной в скобках,

K – безразмерная постоянная.

.

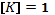3 этап. Составим уравнение размерностей

.

Учитывая, что , получим уравнение размерностей

(3)

4 этап. Воспользуемся таблицей размерностей механических величин

(см. таблицу раздела III)

Подставляя размерности механических величин в уравнение размерностей (3), получим

.

Возведём степени в соответствующую степень и перемножим степени с одинаковыми основаниями. Уравнение размерностей примет вид:

.

= . (4)

Уравнение одно, а неизвестных три. Можно ли найти 3 неизвестных имея одно уравнение? Да, если из него можно получить 3 уравнения. Как? Необходимо приравнять показатели степеней при одинаковых основаниях. Т. е. необходимо «снять верхушки». Получим:

(5)

Система (5) трёх уравнений первой степени с тремя неизвестными эквивалентна уравнению (4).

Примечание к этапу 4

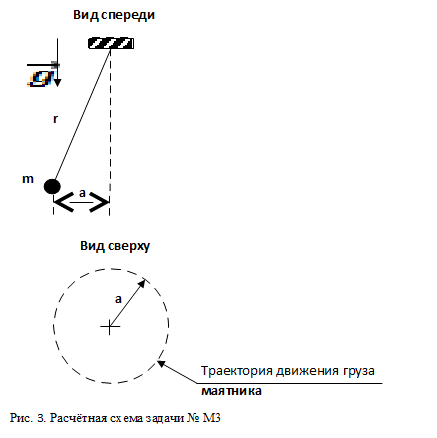
Е. В данной работе используется система размерностей длина, время, энергия (LTE). Использование системы размерностей длина, время, масса (LTM) принципиально ничего не меняет.

5 этап. Решим систему (5)

В данном случае система (5) имеет вид системы Гаусса, и её решение не вызывает трудностей.

Получим

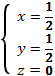(6)

6 этап. Подставим найденные значения x, y, z в выражение (2)

Подставляя найденные значения x, y, z в выражение (2), получим

. (7)

7 этап. Предположим, что K=1

Предположим, что K=1, получим:

Примечание к этапу 7

Ж. Предположение этапа 7 не всегда справедливо и требует дополнительного исследования методами, выходящими за рамки «универсального алгоритма».

8 этап. Доведем результат до числа

Доведем результат до числа:

r = 6400 км = 6,4 · 10⁶ м

g = 10 м/с²

v = (rg)^0,5 = (6,4 · 10⁶ ·10)^0,5 = 8 · 10³ м/с = 8 км/с

Ответ: v = (rg)^0,5 = 8 · 10³ м/с = 8 км/с

9 этап. Анализ решения задачи

Будет ли первая космическая скорость зависеть от массы спутника?

Итоговая формула (ИФ8) показывает, что первая космическая скорость от массы спутника не зависит! Показатель степени массы (m) в формуле размерностей равен нулю (см. первую формулу этапа 6).

Математический аппарат универсального алгоритма анализа размерностей сам скорректировал наше допущение о перечне определяющих параметрах данной задачи и исключил из этого перечня массу спутника.

На этом решение задачи с использованием АР на втором уровне считается завершённым.

При постановке рассмотренной задачи педагог намеренно ввёл «лишний» определяющий параметр – массу. Такой педагогический приём можно назвать «Преднамеренное введение лишнего определяющего параметра».

Примечания к этапу 9

З. Анализ решения задачи можно считать нестандартным этапом (творческим).

В рамках этого этапа не только осуществляется анализ итоговой формулы, но и выявляются аналогии с другими задачами, формулируется постановка новых (в том числе более общих) задач.

На этом этапе выдвигаются предположения, многие из которых могут оказаться плодотворными. Используются индуктивные формы мышления. В связи с этим этот этап выходит за рамки понятия «анализ».

На этапе 9 физическая интуиция исследователя так же важна как и на этапе 1.

И. При решении научных или учебных задач лишние определяющие параметры могут оказаться введёнными непреднамеренно.

Можно просто сообщить учащемуся о том, что «первая космическая скорость не зависит от массы спутников». Но если поставить задачу в такой форме: «Показать, что первая космическая скорость не зависит от массы спутников», то эффективность обучения во втором случае будет выше. В этом случае учащийся сам обнаруживает группу явлений, имеющих общее свойство: первая космическая скорость любого астрономического объекта (центрального тела) не зависит от массы спутника, а зависит от массы астрономического объекта. При этом подразумевается, что масса спутника во много раз меньше массы центрального тела.

Случай соизмеримых масс спутника и центрального тела (двойная звёзда) представлен в работе [3].

II. Использование универсального алгоритма анализа размерностей при решении задач механики

Задача № М2. Найти формулу для круговой (циклической) частоты плоских колебаний (ω) математического маятника, используя универсальный алгоритм анализа размерностей. Потерями, связанными с трением в точке подвеса и сопротивлением воздуха, пренебречь.

Решение

Предложенное ниже решение, основанное на универсальном алгоритме анализа размерностей, изложено не так подробно, как решение предыдущей задачи.

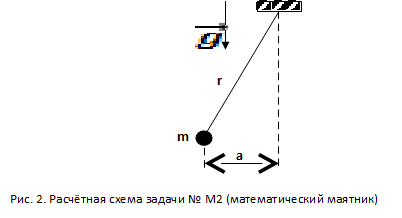
Схема математического маятника представлена на рис. 2.

Поскольку потери энергии маятника, связанные с сопротивлением, отсутствуют, то маятник будет совершать плоские незатухающие колебания.

Предположим, что круговая частота колебаний (ω) маятника зависит от его длины , ускорения свободного падения (g) и его массы (m):

(1)

Представим размерности всех вышеупомянутых величин, используя таблицу раздела III. Получим

; (2)

Составим уравнение размерностей физических величин, используя (2):

. (3)

Приравнивая показатели степеней с одинаковыми основаниями, получим систему трёх линейных уравнений относительно искомых показателей степеней (x, y, z):

. (4)

Решая эту систему, получим

x 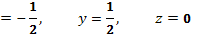. (5)

Подставляя (5) в (1), получим

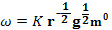. (6)

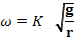. (7)

Решение задачи другими способами (а также эксперимент) даёт значение 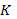, равное единице при следующем допущении.

Допущение. Плоские колебания математического маятника имеют малую амплитуду (а).

Т. е.

а << r .

С учётом этого формула (7) примет окончательный вид:

. (ИФ8)

Определение 1. Колебания (периодические явления), имеющие одинаковую круговую частоту (, называются изохронными.

Т. е. колебания данного маятника с разными амплитудами в пределах принятого допущения (амплитуды колебаний малы) изохронны.

На языке АР это суждение означает: данное физическое явление «автомодельно» по критерию подобия (Е) при выполнении условия

Е = << 1 ,

где

Е – безразмерный параметр (критерий подобия), учитывающий геометрические особенности явления.

Анализ (ИФ8)

Отметим, что масса (m) в (6) имеет показатель степени, равный нулю. Это означает, что круговая частота колебаний (ω) маятника не зависит от его массы.

Учитывая итог решения предыдущей задачи, здесь напрашивается следующий вопрос: «Справедливо ли обобщение о том, что любое движение пробного тела в поле тяготения (свободное или с идеальными связями) не зависит от массы пробного тела?»

Сама постановка такого вопроса имеет фундаментальный характер. Обобщая наши знания о движении тел в гравитационном поле, основанные на решениях рассмотренных задач, можно утверждать, что движение пробного тела в поле тяготения не зависит от массы пробного тела не только тогда, когда тело свободное, но и в том случае, когда его движение ограничено идеальными связями или опорами (пример – математический маятник). Это обобщение есть результат использования универсального алгоритма анализа размерностей.

Приём преднамеренного введения учителем лишнего определяющего параметра педагогически обоснован. В результате решения такой задачи учащийся сам получает результат, обобщающий его познания в физике.

Задача № М3. Найти формулу для угловой скорости кругового движения (ω) математического маятника в поле тяготения (т. е. движение груза маятника осуществляется по окружности), используя универсальный алгоритм анализа размерностей. Потерями, связанными с трением в точке подвеса и сопротивлением воздуха, пренебречь.

Решение

Схема математического маятника, совершающего движение по конической поверхности, представлена на рис. 3.

Поскольку потери энергии маятника, связанные с сопротивлением, отсутствуют, то траектория груза маятника будет окружностью с постоянным радиусом (а). Маятник будет совершать незатухающие периодические движения по конической поверхности.

Решение этой задачи с использованием универсального алгоритма анализа размерностей ничем не отличается от решения предыдущей, поскольку в этой задаче управляемый параметр тот же самый (круговая частота периодического движения) и никаких новых управляющих параметров не появилось. Оно приводит к той же формуле (7) предыдущей задачи, которая здесь имеет номер 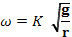(1):

. (1)

Т. е. такое движение также изохронно.

Решение задачи другими способами (а также эксперимент) также даёт значени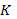е , равное единице, если учитывать допущение, указанное выше.

Формула (1) примет вид, аналогичный формуле (ИФ8) предыдущей задачи:

. (ИФ2)

На языке анализа размерностей это суждение означает: «данное физическое явление автомодельно по критерию подобия (Е) при малых амплитудах

Е = << 1 ,

где

Е – безразмерный параметр (критерий подобия), учитывающий геометрические особенности явления,

а – радиус окружности движения груза маятника (он также назван амплитудой) при конических колебаниях».

Таким образом, выявлена аналогия между рассмотренными двумя разновидностями периодического движения математического маятника (плоским и коническим). Оба эти движения изохронны. Колебания математического маятника с малыми амплитудами изохронны независимо от того, являются ли они плоскими или коническими.

Кроме того, нами установлено, что явления, рассмотренные в задачах № М1-3, не зависят от массы тел, движение которых рассматривается.

Примеры использования анализа размерностей в школьной геометрии представлены в работе [4].

III. Классификация механических величин по их размерности

f – физическая (в данном случае механическая) величина.

IV. Заключение

1. Предложенный универсальный алгоритм анализа размерностей, пригодный для использования в средней школе, позволяет получать итоговые формулы – решения физических задач – с точностью до безразмерного постоянного множителя.

2. Универсальный алгоритм анализа размерностей обладает эвристическим свойством: учащийся сам открывает новые для себя формулы. Алгоритм позволяет добывать новые знания умением его применять.

3. Универсальный алгоритм анализа размерностей обладает свойством «обратной связи»: математический аппарат алгоритма позволяет установить некорректность постановки физической задачи, связанной с выбором перечня управляемых параметров. Таким образом, стиль решения учебной задачи физики приближается к стилю решения инженерных и научных задач.

4. Учащийся активно использует математический аппарат алгоритма. Это укрепляет понимание учащимся необходимости совместного использования физики и математики и способствует лучшему усвоению материала обоих предметов.

5. Предложенный алгоритм анализа размерностей развивает физическую интуицию, поскольку включает необходимость правильной постановки задачи.

6. Использование алгоритма приводит к неожиданным новым уровням обобщения и аналогиям, которые при решении задач физики иными методами не выявляются.

7. Анализ размерностей позволяет помочь учащемуся лучше понять различие между безразмерными величинами и величинами, имеющими размерность. Учащийся осознаёт ключевую роль размерностей физических величин для понимания физических явлений.

8. Возможности универсального алгоритма анализа размерностей можно расширять, обучая искусству его применения.

Литература:

1. Седов Л.И. Методы подобия и размерности в механике. – М.: Наука, 1977. – 440 с.

2. Баренблатт Г.И. Автомодельные явления – анализ размерностей и скейлинг: Пер. с англ.: Учебное пособие / Баренблатт Г.И. – Долгопрудный: Издательский Дом «Интеллект», 2009. – 216 с.

3. Мазейкина М. Ю., Неграш А. С. От кинематических законов Галилея и Кеплера к динамическим законам Ньютона: методика изложения классической механики // Молодой учёный №5 (40). Том 3. – С. 452-460.

4. Неграш А. С., Мазейкина М. Ю. Использование анализа размерностей в геометрии // Педагогическое мастерство: материалы междунар. заоч. науч. конф. (г. Москва, апрель 2012 г.) в 2 томах. Том 1. – М.: Буки-Веди, 2012. – С. 165-169.