Использование обратных математических моделей в задачах адаптивного управления

Вопросы управления экономическими системами в настоящее время являются особенно актуальными в связи с преодолением последствий недавнего экономического кризиса. Особенно важным становится умение компаний приспосабливаться к быстро меняющимся условиям рынка, вследствие чего применяются методы адаптивного управления (ср. [1, с. 184]).

Рассмотрим модель бизнес-процессов (ср. [1, с. 18]), включающую в себя сетевую, потоковую, математическую (операторную) модели и характеристики бизнес-процессов, как кортеж вида:

, ,

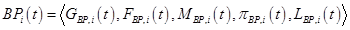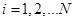где 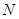 - общее число бизнес-процессов,  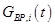- сетевая (графовая) модель 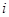-го бизнес-процесса;  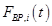- потоковая модель 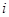-го бизнес-процесса;  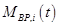- математическая модель 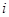-го бизнес-процесса;  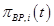- параметры (характеристики) моделей 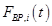,  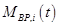и некоторых других для 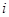-го бизнес-процесса;  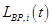- модель ограничений на ресурсы 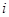-го бизнес-процесса.

Бизнес-процесс 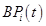 и порождающие его модели зависят от времени  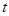и эта зависимость позволяет отнести модели к динамическим. Множество моделей  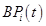порождает множество базовых бизнес-процессов .

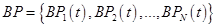В качестве математической модели бизнес-процессов 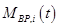могут быть использованы модели самых разных видов и предназначений. Так в качестве таких моделей могут быть использованы: модели задач математического программирования; модели задач оптимального управления; модели задач логистики; модели задач прогнозирования; модели задач построения моделей и т.д.

В общем случае модель 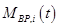 представляет собой отображение:

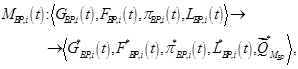
где 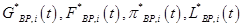 – это преобразованные модели бизнес-процесс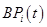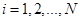а , , а 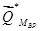 – вектор, характеризующий такое преобразование (отображение). Так в качестве преобразованных моделей и вектора  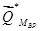могут выступать: «оптимальные» модели (потоки, планы выпуска продукции, планы транспортировки и др.) и соответствующие этим потокам и планам показатели (прибыль, затраты на транспортировку и др.); «оптимальные» выходы технологических операций и соответствующие им характеристики; планы закупок сырья, приобретения ресурсов и их характеристики и т.д.

Для более простых экономических систем модель 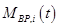 преобразует входные потоки процесса  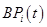(такие как 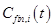,  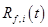и др.) и параметры  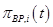в выходные потоки (такие, как 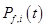,  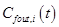и др.). Таким образом, в этом случае математическую модель можно представить в виде:

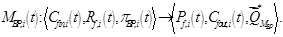
Такой подход к построению моделей бизнес-процессов позволяет не только оценить эффективность отдельных (частных) бизнес-процессов, но и выделить в общем эффекте эффекты от каждой из составляющей модели бизнес-процессов: потоков, параметров, математической модели и т.д.

Очевидно, что наряду с управлениям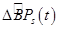и  (или 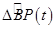) могут быть использованы также управления параметрами ЭС (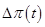) и обобщенными потоками (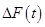). Соответствующие этим управлениям подходы могут быть названы структурным, параметрическим и координатным управлениями.

На практике может быть полезным объединить (или разъединить, выделить) некоторые из управлений. Например, выделить из 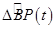 в самостоятельные управления – управления  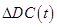(определяющее изменение структуры бизнес-процесса) и  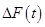(определяющее изменение потоков бизнес-процесса). 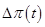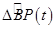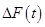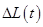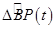Отличительной особенностью этих корректирующих воздействий и задачи управления бизнес-процессами на их основе является то, что коррекция, например,  может привести к появлению корректирующих управлений вида  и , а коррекция  – к  и 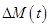 и т.д.

Пример. Рассмотрим в качестве примера торговую сеть. Тогда, например, задача управления торговой сетью, связанная с управлением ассортиментом при изменяющемся спросе может быть представлена следующим образом. Требуется найти такое управляющее воздействие на сеть: 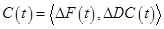, которое доставляет экстремум некоторому функционалу 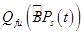. При этом сигналом для принятия решения по корректировке бизнес-процесса  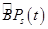может быть значение показателя  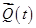(или пары с учетом риска 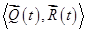) за границы области допустимых (или желаемых) значени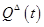й  (или 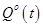). Возможно, таким сигналом будет отклонение обобщенного потока  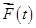от его допустимых (желаемых) значени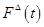й  (или 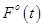) и т.д. Например, наблюдается снижение спроса на некоторый товар (товарную группу). Это снижение спроса проявляется в изменении показателей  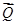и потоков  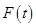бизнес-процесса  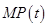(реализации товара). Как только обнаружился (или прогнозируется, ожидается) эффект отклонения значений показателей или потоков от желаемых (или плановых, допустимых) значений, необходимо решить следующие задачи.

1. Выбрать из множества допустимых управлений 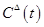 одно из них ().

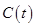2. Найти новое состояние бизнес-процесса 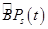, полученное после применения к нему управляющего воздействия 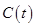. Условно этот бизнес-процесс может быть обозначен так: 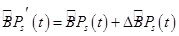, где бизнес-процесс  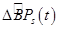соответствует управлению .

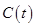3. Проверить, если бизнес-процесс 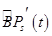 является реализуемым (т.е. удовлетворяет ограничениям на ресурсы, финансовые потоки и т.д., принадлежит области допустимых значений для всех его составляющих), то для него следует вычислить значения показателей  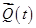(или с учетом рисков ).

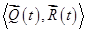4. Перебирая последовательно все возможные значения управлений 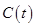 и производя каждый раз для них решения задач 1-3, следует выбрать лучшее управление  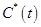по критерию  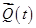(или 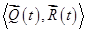,  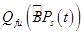и т.д.).

Очевидно, что в общем случае в корректирующее управление 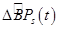 следует включить не только бизнес-процессы непосредственно изменяющие процесс 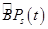, но и некоторые вспомогательные бизнес-процессы, связанные с выработкой управлений .

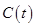Сделаем замечания к рассмотренному примеру.

Замечание 1. Во множество управляющих воздействий 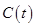 наряду с коррекциям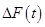и  и 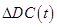, отвечающими за изменения обобщенных потоков и структуры, могут быть введены также коррекции для параметров 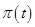, ограничений 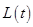, модели  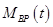и т.д.

Замечание 2. Нахождение наилучшего управления 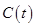 как результата решения последовательности задач 1-4 носит характер дискретной оптимизационной задачи. Перебор вариантов для управлений  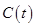можно сделать направленным, если, например, воспользоваться принципом «движения от источника возмущений» (принципом ДИВ), реализующим решение обратной задачи [2], т.е. в первую очередь попытаться изменять 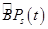,  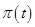и 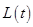 вблизи того места в бизнес-процессе, где обнаружено возмущение. Например, если обнаружено снижение объёмов продаж в торговой сети, то, прежде всего, необходимо попытаться изменить процесс (например, реализации продукции) и его характеристики и параметры, а уже затем, в случае неудовлетворительных управлений 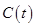, попытаться изменять предшествующие ему бизнес-процессы.

Замечание 3. Поскольку в общем случае задача изменения структуры бизнес-процесса 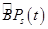 является задачей плохо формализуемой, то, думается, что лучшим подходом для выбора управления  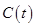будет человеко-машинный подход, когда часть задач (наименее формализованных) ляжет на плечи аналитика (оператора), а оставшаяся часть (хорошо формализованные задачи) будет решаться с помощью соответствующих программ. Некоторые из структурных изменений можно заложить заранее в качестве возможных корректур 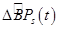, тогда проведение анализа на предмет использования одной из них (наиболее эффективной) может осуществить программа выработки управлений.

Замечание 4. Решение задач, связанных с изменением потоков бизнес-процессов 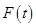, может быть осуществлено с использованием, например математических моделей процессов закупки сырья, производства,  доставки и реализации продукции, которые связывают функциональными зависимостями выходные и входные потоки соответствующих бизнес-процессов и являются, таким образом, обратными по отношению к моделям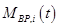и имеют вид:

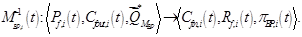       Решению экономических проблем на основе обратных моделей и посвящено наше исследование.

Математическую модель торгово-производственного предприятия можно построить из моделей отдельных процессов следующим образом:

,

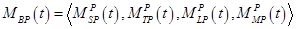где 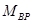 – математическая модель четырех процессов предприятия в целом. Базисные бизнес-процессы  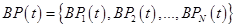(для вышерассмотренного производственно-торгового предприятия 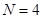) могут быть включены в структурированную модель с помощью операции сцепления со сдвигом во времени –  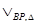следующим образом:

,

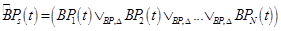где 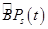 – бизнес-процесс, полученный из бизнес-процессов множества  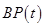с помощью операции  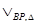и в котором проведена операция согласования всех внутренних и внешних потоков. Заметим, что присутствие одного и того же индекса «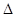» в знаках операции  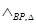в последовательной цепочке для записи  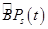не говорит о том, что смещения во времени бизнес-процессов в парах являются одинаковыми. Распишем структурированный бизнес-процесс  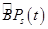через его составляющие следующим образом:

,

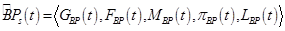где зависимость от времени всех составляющих процесса и самого этого процесса говорит об изменении их с течением времени (во времени), в том числе и математической модели процесса – .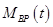

Такое изменение во времени представляется особенно актуальным, поскольку бизнес-процесс следует приспосабливать (адаптировать) к изменяющимся внешним и внутренним условиям его протекания.

Литература

1.                  Управление экономическими системами. Процессный подход : Монография. / А.А. Наумов, М.А. Максимов. -Новосибирск: ОФСЕТ, 2008. - 300 c.

2.                  А. А. Наумов, Е. А. Мазутская,  Методы обратных задач в экономических исследованиях  // VI Всесибирский конгресс женщин-математиков: Материалы Всероссийской конференции, 15-17 января 2010 г. / Красноярск: РИЦ СибГТУ, 2010, С. 299-303.