Поиск решения как средство решения задач оптимизации и теории игр

Уровень развития информационных технологий, современные концепции образования, необходимость развития на всем протяжении жизни для адекватности современным условиям заставляет пересмотреть и сами технологии, применяемые в образовательном процессе, выбирая из них, в первую очередь те, которые повышают эффективность и качество обучения. обеспечивают мотивы к самостоятельной познавательной деятельности; способствуют углублению межпредметных связей за счет интеграции информационной и предметной подготовки.

Процедура «Поиск решения» (MS EXCEL) представляет собой мощный инструмент для выполнения сложных вычислений. Она позволяет находить значения переменных, удовлетворяющих указанным критериям оптимальности, при условии выполнения заданных ограничений. Наилучшие результаты она позволяет получить для задач выпуклого программирования. Такие результаты оптимизации оформляются в виде отчетов трёх типов: результаты, устойчивость и пределы.

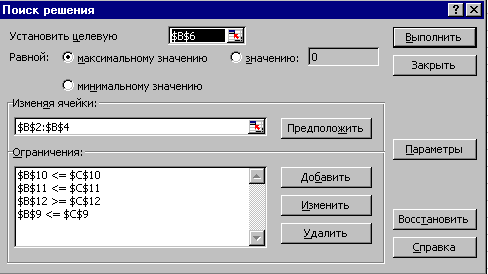
Для решения задачи оптимизации необходимо на рабочем листе Excel создать таблицу исходных данных, в которой должны отображаться формулы. Затем запустить процедуру поиска решения, дав команду Сервис (Поиск решения), и в появившемся диалоговом окне заполнить поля: установить целевую ячейку; изменяя ячейки; ограничения.

Целевая ячейка — ячейка на рабочем листе с таблицей исходных данных, куда занесена формула целевой функции. Изменяемые ячейки — ячейки из таблицы исходных данных, отражающие значения переменных, которые необходимо найти в результате оптимизации. Ячейки не должны содержать формулы, их значения должны влиять на значение целевой ячейкиⁱ. Ограничения - задаются посредством кнопки Добавить и отражают связь формул ограничений с их свободными членами.

Рис. 1. Диалоговое окно Поиск решения

Установить переключатель Равной: максимальному значению. В поле Изменяя ячейки ввести диапазон ячеек, отражающий первоначальные значения переменных. Используя кнопку Добавить, ввести в поле Ограничения все ограничения, предусмотренные задачей.

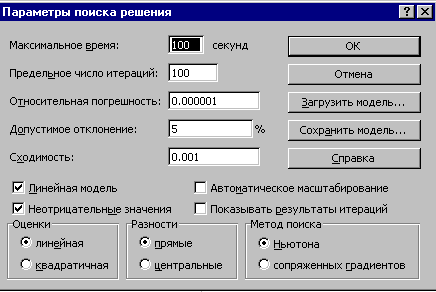
В диалоговом окне Добавление ограничения в поле Ссылка на ячейку указать ячейку, содержащую формулу ограничения, затем в следующем окне из раскрывающегося списка выбрать логический оператор, отражающий отношение между формулой и свободным членом и в поле Ограничение ввести ссылку на ячейку со свободным членом данного ограничения. Получится запись как на рис.1. В диалоговом окне Поиск решения нажать кнопку Параметры, установить флажок Линейная модель и задать условия неотрицательности переменных, установив флажок Неотрицательные значения в диалоговом окне Параметры поиска решения. Нажать кнопку ОК и перейти в диалоговое окно Поиск решения.

Рис. 2. Диалоговое окно Параметры поиска решения

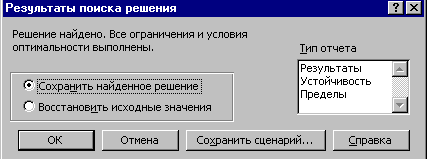
Далее в диалоговом окне Поиск решения нажать кнопку Выполнить и проанализировать полученные отчеты.

Рис.3. Диалоговое окно Результаты поиска решения

Анализируя полученное решение, следует принимать во внимание факторы, влияющие на целевую функцию и соответственно снижающие или увеличивающие ее значение.

Матричные игры в чистых стратегиях определенной размерности можно автоматизировать в табличном процессоре MS EXCEL. При этом используются встроенные функции: МАКС, МИН, ЕСЛИ и ПОИСК РЕШЕНИЯ.

Рассмотрим для примера виртуальную игру в чистых стратегиях, приближенную к практическим боевым действиям. В ходе проведения боевой операции возникла следующая ситуация. Противник продвигается с запада на восток по одному из трех возможных направлений 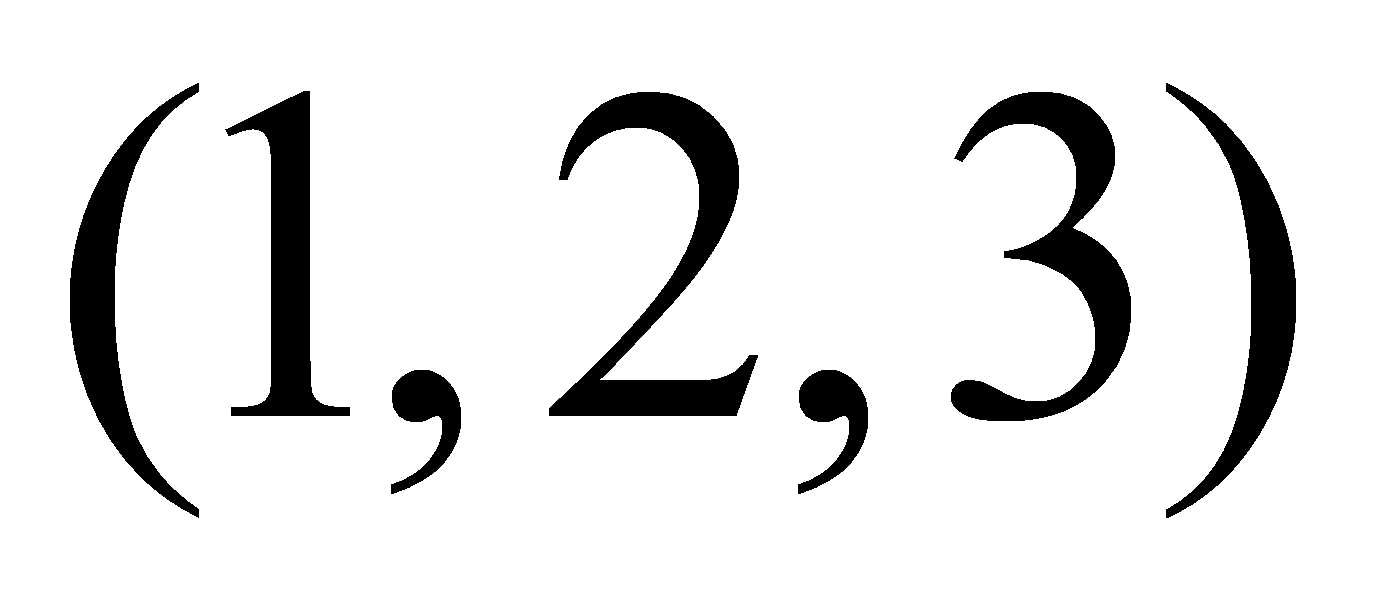. Группе захвата поставлена боевая задача: выти наперерез противнику, навязать им открытый бой и одержать победу над ним. Группа захвата имеет также три маршрута движения 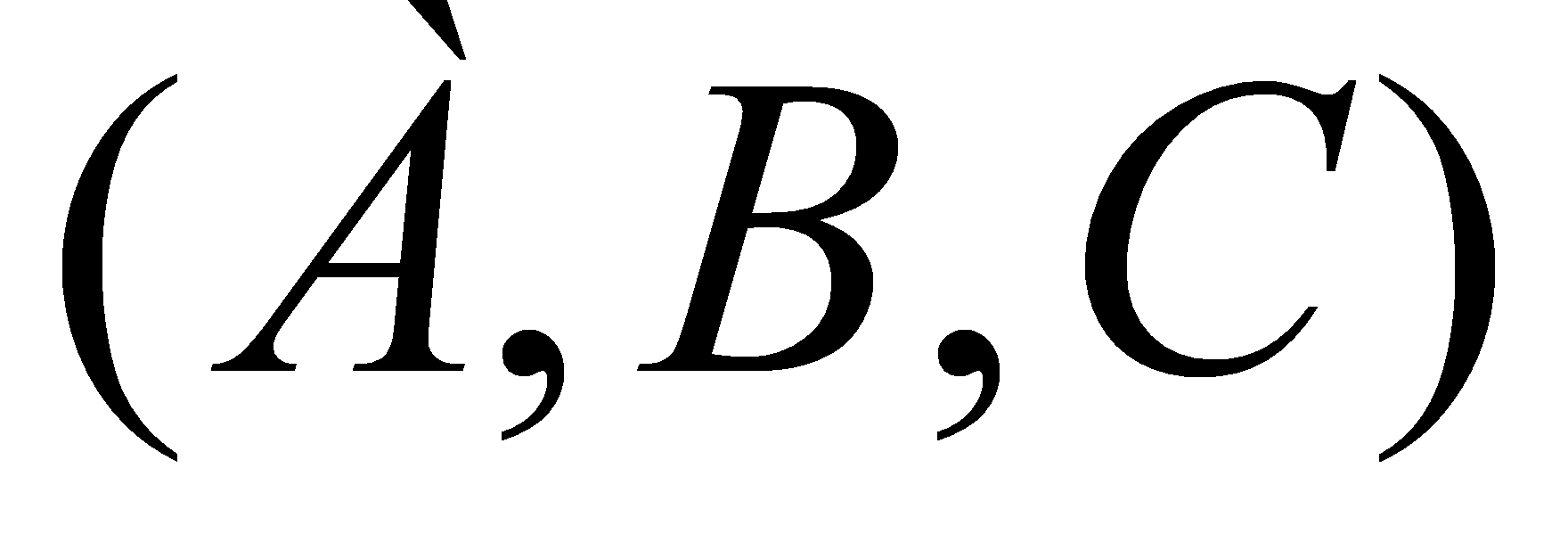. Пересечение путей движения обеих групп определяет место проведения боя. Таким образом, существует 9 возможных участков столкновения. Все они располагаются на разных относительных высотах, приведенных в таблице:

Таблица 1

Высоты предполагаемого боя боевой операции

Противник

Группе захвата выгоднее навязать открытый бой противнику на местности с наименьшей относительной высотой. Противник чувствует себя более уверенно и безопасно в горах. Участки предполагаемого боя имеют разные высоты, указанные в таблице. Необходимо определить, какой маршрут движения группы захвата оптимален.

В качестве выигрыша для группы захвата в каждом случае реализации выбора места схватки рассмотрим высоту данной местности, взятую с обратным знаком, так как увеличение высоты стратегически не выгодно для нее и, следовательно, выигрыш меньше.

Сформируем в соответствующих ячейках таблицу высот предполагаемой боевой операции.

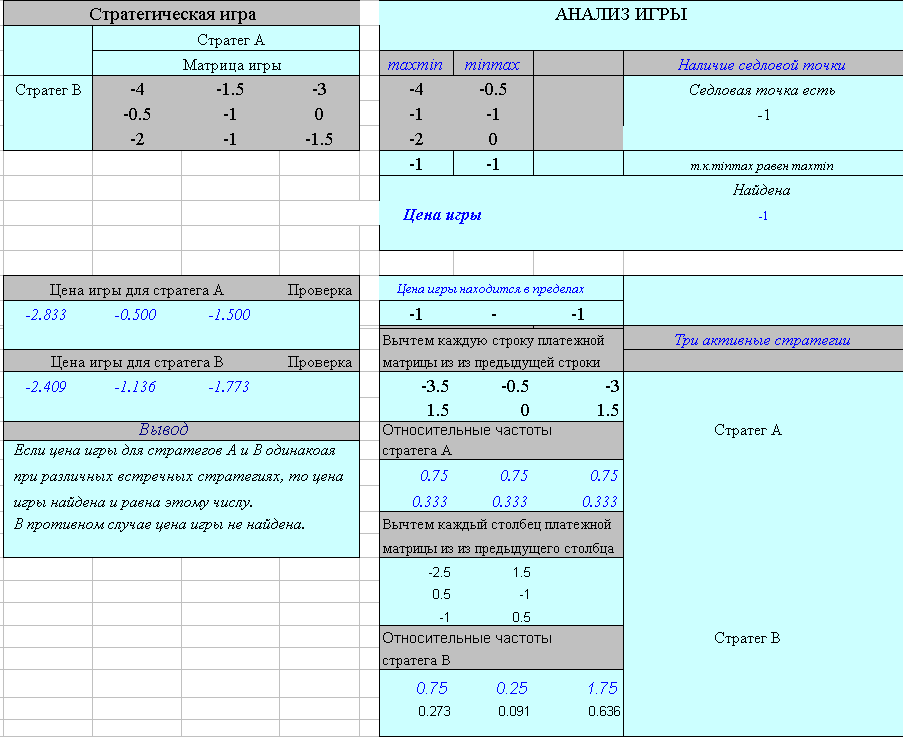
Рис. 4. Рабочий лист Excel с записью таблицы исходных данных и
решением задачи о виртуальных боевых действиях

Для каждого варианта решения определим наиболее неблагоприятный исход в зависимости от действий противника, а затем из полученных значений выигрышей выберем максимальный по принципу «лучший из худших». Для этого анализируются все строки матрицы, соответствующие стратегу B, и с помощью встроенной функции «МИН» выбираются наименьшие элементы. Далее с помощью функции «МАКС» находится максимальный элемент из них. Таким образом, находится MAXMIN. Аналогично для нахождения MINMAX проводится анализ по столбцам.

С помощью логической функции «ЕСЛИ» определяется один из двух вариантов ответов: цена игры найдена или нет. В случае положительного ответа по ссылке на соответствующую ячейку она показывается на экране. Используя данные функции и Поиск решения, можно построить решение для смешанных стратегий.

Литература:

1. Акулич И.Л., Математическое программирование в примерах и задачах.- М.: Высшая школа, 1986.-317 с.
2. Вентцель Е.С. Элементы теории игр. М.: Наука, 2008.-360 с.
3. Вентцель Е.С.Исследование операций.- Сов.радио, 1972.-551 с.
4. Грешилов А.А. Математические методы принятия решений — М.: МГТУ им. Н.Э. Баумана, 2006. – 320 с.
5. Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр. Учебное пособие для университетов. М.: Высш.шк., Книжный дом «Университет, 1998. -304с.
6. Покорная О.Ю. О выборе оптимальных стратегий в планировании боевых операций. Всероссийской научно-практическая конференция «Инновации в авиационных комплексах и системах военного назначения». Воронеж, ВАИУ, Ч.10, 2009, с.194-198.