Кинематическое управление шестиногим шагающим роботом



В данной работе строится кинематическая модель шестиногого робота, рассматривается обратная задача кинематики построенной модели в двух формах: аналитической и численной. Затем решается задача генерации походки в случае движения по ровной поверхности, в рамках которой находятся траектории движения ног гексапода.

Ключевые слова: робототехника, гексапод, шагающий робот, кинематическое управление.

Введение

История робототехники берет начало с давних времен. Еще в 1500 году Леонардо да Винчи изобрел механического льва, разворачивающего герб Франции при въезде короля в город. С развитием технологий роботы стали применяться в промышленности и в настоящее время всё чаще заменяют человека в работах, требующих больших физических усилий или проходящих в неблагоприятных условиях. Шестиногий шагающий робот сочетает в себе устойчивость конструкции и простоту управления, что позволяет использовать его во многих отраслях человеческой деятельности: при лесозаготовке, поиске мин или в качестве средства передвижения для людей с ограниченными движениями.

Кинематика робота-гексапода

Объектом исследования является шестиногий шагающий робот с платформой в виде равностороннего шестиугольника, в углах которого располагаются трехзвенные конечности.

Конечность робота состоит из бедра, голени, коленного и бедренного суставов. Так как сочленения робота в отличие от реальных суставов имеют только одну степень свободы, бедренный сустав разделен на два, между которыми находится промежуточное звено. Бедренный сустав 1 (между платформой и промежуточным звеном) вращается вокруг вертикальной оси. Бедренный сустав 2 (между промежуточным звеном и бедром) и коленный суставы вращаются вокруг горизонтальной оси.

Введем две системы координат: систему координат платформы и систему координат конечности . Центр первой из них расположен в центре платформы робота, плоскость совпадает с плоскостью платформы, ось направлена в точку прикрепления первой ноги, ось направлена вверх относительно земли перпендикулярно платформе (предполагаем, что робот не переворачивается). Центр второй из них расположен в точке прикрепления ноги, плоскость также совпадает с плоскостью платформы, ось направлена от центра платформы к точке прикрепления ноги, ось направлена, как и .

Координаты стоп (оконечностей ноги) робота в системе координат конечности имеет следующий вид:

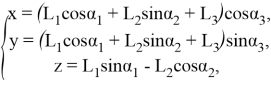(1)

где

− x, y, z — координаты стопы,

− L₁, L₂, L_{3 —} длины бедра, голени и промежуточного звена соответственно,

− α_{1 —} угол между бедром и плоскостью ,

− α_{2 —} угол отклонения голени от вертикальной оси,

− α_{3 —} угол отклонения ноги от .

Решение обратной задачи кинематики

В системе уравнений (1) мы получили выражение координат стопы через углы сочленений ноги, задачи подобного типа принято называть прямой задачей кинематики [1]. После этого естественно задаться вопросом о возможном обратном преобразовании координат стопы в углы ориентации, то есть провести решение обратной задачи кинематики. Данное решение можно искать двумя способами: аналитически, выразив уравнения для нахождения значений углов в сочленениях из системы (1), и численно, разбивая время на конечные промежутки.

Аналитический метод

Используя геометрический подход [1], разрешим систему (1) относительно α₁, α₂, α₃. В общем случае решение данной задачи не единственно, но выберем решение, которое соответствует верхнему расположению коленного сустава, как более естественное:

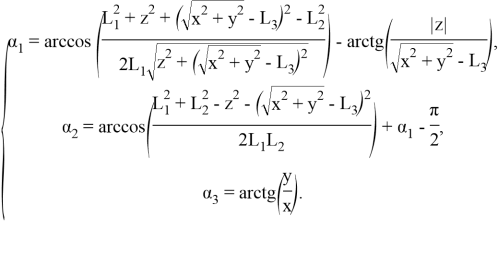
Последовательно вычисляя α₃, α₁, α₂, найдем искомое решение системы.

Численный метод

Для решения этой задачи выполним дифференцирование системы (1):

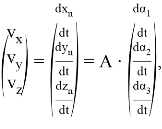
где

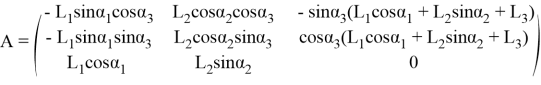
и _— составляющие вектора скорости движения стопы. Разрешим систему (3) относительно углов:

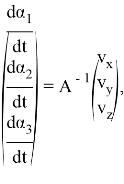
где

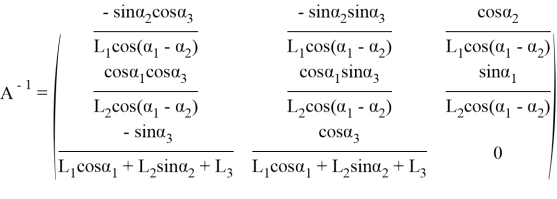
Обратная матрица A⁻¹ точно существует при следующих условиях:

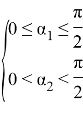
Используя метод Эйлера [2], получим численное решение обратной задачи кинематики:

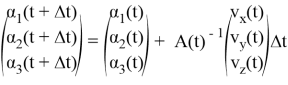(4)

Таким образом, задавая зависимость скорости стопы от времени, будем находить необходимые для ее достижения углы в сочленениях.

Параметризация походки

Для генерации походки разобьем конечности на две группы: с четными и нечетными номерами. В то время как одна группа ног располагается в воздухе, что соответствует фазе переноса, другая группа ног находится на земле, то есть в фазе опоры. Такая походка соответствует насекомым (например, муравьям и мухам), поэтому называется инсектовидной. Каждая фаза длится одинаковое время T. Разница фаз групп ног также составляет T.

Рассмотрим шаговый цикл ноги гексапода. Траектория конечности в локальной системе координат представляет собой замкнутую кривую. Данную кривую можно условно разделить на две части, которые соответствуют фазе переноса ноги и фазе опоры ноги. При переносе конечности из одной точки в другую выбор траектории может быть осуществлен произвольным образом, так как стопа находится в свободном движении. В данной работе в качестве траектории переноса ноги используется полуэллипс. В фазе опоры нога движется по опорной поверхности вдоль прямой в направлении, обратном движению всего механизма. Траектория указана на рисунке 1.

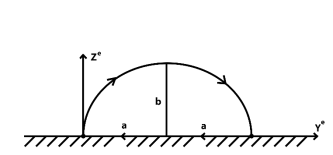
Рис. 1. Траектория движения стопы конечности

Фаза переноса

Параметризация эллипса в связанной с ним системе координат выглядит следующим образом:

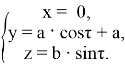
Траектория фазы переноса лежит в плоскости, параллельной и отстоящей от начала координат по оси на . Также для того, чтобы конечные точки дуги эллипса располагались на земле, производится смещение по оси на высоту платформы робота. Уравнения в системе координат конечности имеют следующий вид:

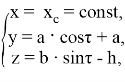
где:

−

− T — полупериод одного шага, то есть время, за которое происходит перестановка одной тройки ног,

− h — расстояние от платформы гексапода до земли,

− a и b — большая и малая полуоси эллипса соответственно.

Зависимость параметра τ от времени принята на основе работы [3]. Такой ее вид обеспечивает постановку ноги на землю с нулевой конечной скоростью, что позволяет избежать ударов.

Идея организации походки заключается в том, что плоскость траектории движения каждой стопы ставится под таким же углом к оси (ось системы координат платформы робота), как и направление движения механизма к этой оси. Угол, необходимый для постановки i-ой ноги в нужном направлении, равен:

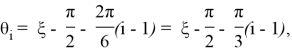
где ξ — угол между направлением движения гексапода и осью .

Для постановки плоскости траектории стопы гексапода нужным образом, проведем следующие действия: параллельным переносом сдвинем эллипс в плоскость , домножим на матрицу поворота на угол θ, сдвинем эллипс по оси до достижения его начальной точкой точки . Итоговый вид параметризации фазы переноса траектории стопы:

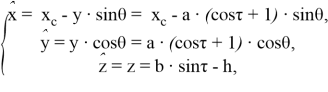(5)

где .

Продифференцируем систему (5) для нахождения скоростей, используемых в методе Эйлера:

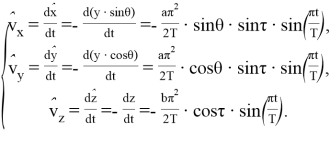(6)

Фаза опоры

Для нахождения части траектории, соответствующей фазе опоры ноги, соединим конечные точки эллипса. Следует заметить, что движение по прямой осуществляется за то же время T, что и по дуге. Уравнение соответствующей прямой можно записать в параметрическом виде:

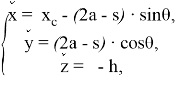(7)

где .

Зависимость параметра от времени выбрана по аналогии с параметром τ, таким образом в граничных точках скорость обращается в ноль, следовательно, проскальзывание отсутствует.

Продифференцируем (7):

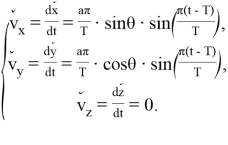(8)

Подставляя в систему уравнений (2) в качестве параметризации из системы (5) и из системы (7), получим аналитический вид выражений углов в сочленениях гексапода от времени для фазы переноса и фазы опоры соответственно. Аналогично, подставляя в систему (4) в качестве параметризации и из систем уравнений (6) и (8) — численный способ получения этих углов.

Проиллюстрируем полученные результаты на примере гексапода со следующими параметрами:

	15 см		3 см
	25 см		2.5 см
	5 см		π/3
	10 см		π/6
	2 с		0

На рисунке 2 показан график зависимости значений углов в сочленениях робота-гексапода от времени в процессе фазы переноса одного шага. График для численного метода решения выглядит на первый взгляд так же, однако вычисляя разность между значениями углов, полученными двумя методами, получим график зависимости ошибки численного метода от времени (рисунок 3).

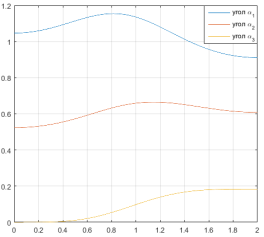
Рис. 2. Значения углов при аналитическом методе решения

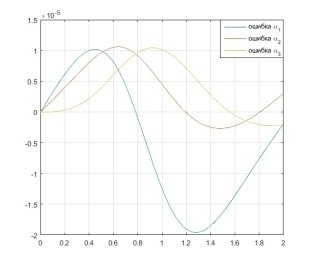
Рис. 3. Ошибка численного метода решения

Теперь рассмотрим иллюстрации процесса движения гексапода. На рисунке 4 представлена визуализация шага робота в системе координат конечности . А на рисунке 5 — пример траектории робота-гексапода (пунктирной линией обозначена траектория центра платформы робота).

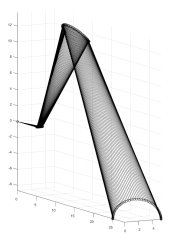
Рис. 4: Визуализация шага

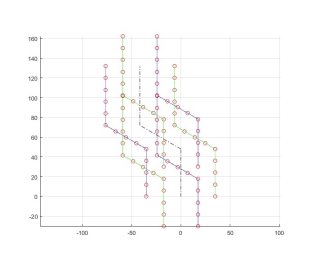
Рис. 5: Визуализация траекторий стоп ног робота (вид сверху)

Заключение

Исследована кинематическая модель робота-гексапода, с помощью которой можно определить координаты стоп в зависимости от обобщенных координат. В двух различных видах решена обратная задача кинематики, что позволяет использовать любой способ нахождения углов в сочленениях по своему усмотрению. В качестве походки выбрана походка, определяемая движением ног по тройкам (инсектовидная). Задана параметризация движения стопы в форме полуэллипса. Найдены соответствующие ей уравнения, которые позволяют осуществлять шаговый цикл в любом направлении.

Литература:

1. John J. Craig. Introduction to Robotics: Mechanics and Control (3rd Edition). Pearson, 2004.
2. Пименов В. Г., Ложников А. Б. Численные методы. Часть 2. Издательство Уральского университета, 2014.
3. Павловский, В.Е., Панченко А. В. Модели и алгоритм управления движением малого шестиногого робота. Мехатроника, автоматизация, управление. — 2012. — № 11. — С.23 –28.