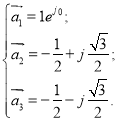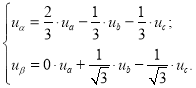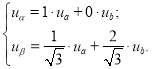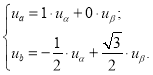Преобразования переменных в системах координат a, b, c и α, β



Для лучшего понимания студентами процесса перехода из одной системы координат в другую дадим проекции одного и того же вектора в двух системах координат a, b, c и α, β (рис. 1).

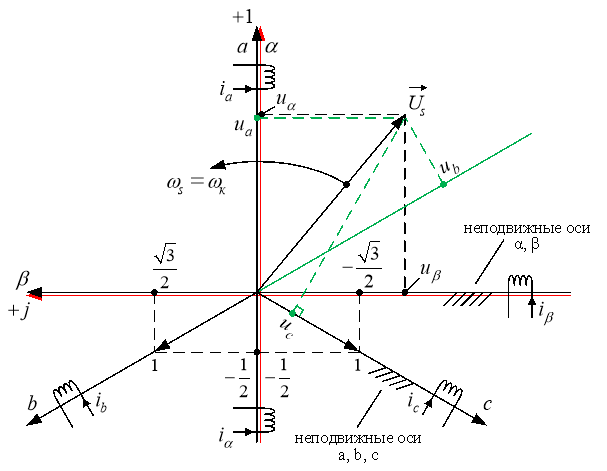
Рис. 1. Проекции вектора в системах координат a, b, c и α, β

В двухфазной системе координат α, β пространственный вектор [1]:

В трехфазной системе a, b, c пространственный вектор определяется по следующей зависимости:

(1)

где , и - единичные пространственные векторы, определяемые:

(2)

Подставим (2) в уравнение (1):

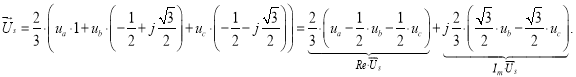
А) Прямой перевод переменных из трехфазной системы в двухфазную: a, b, c → α, β.

Проекции вектора по оси (+1):

Проекции по оси (+j):

Объединим уравнения в систему:

(3)

С помощью полученных уравнений производится переход из одной системы координат в другую: a, b, c → α, β.

В матричной форме система уравнений (3) примет следующий вид:

	=				·
		0
0		0	0	0

Математическая модель прямого преобразования координат (u_a, u_b, u_c → u_α, u_β) в Simulink представлена на рис. 2.

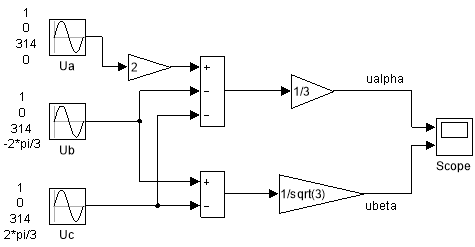
Рис. 2. Прямое преобразование координат u_a, u_b, u_c → u_α, u_β

Математическая модель прямого преобразования в виде матрицы в блоке Gain представлена на рис. 3. Задание матрицы в блоке Gain показано на рис. 4.

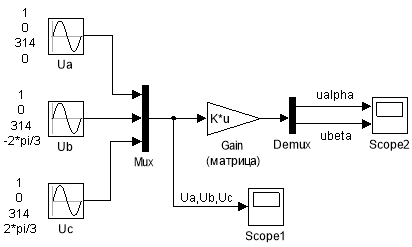
Рис. 3. Прямое преобразование координат u_a, u_b, u_c → u_α, u_β в виде матрицы в блоке Gain

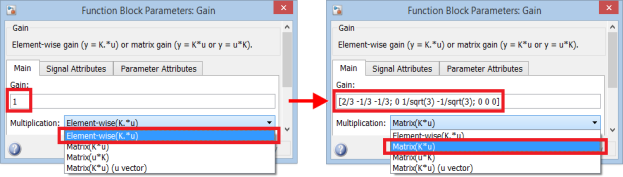
Рис. 4. Задание матрицы в блоке Gain

Задание напряжений u_a, u_b, u_c (рис. 3) и напряжения на выходе преобразователя u_α, u_β приведены на рис. 5 и 6.

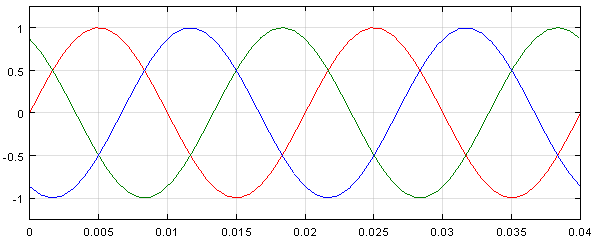
Рис. 5. Графики напряжений u_a, u_b и u_c (Scope 1)

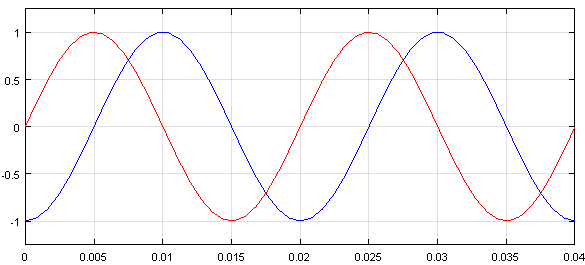
Рис. 6. Графики напряжений u_α и u_β (Scope 2)

При соединении статорной обмотки в «звезду» без нулевого провода:

Из системы уравнений (3):

Тогда система уравнений (3) примет следующий вид:

(4)

Математическая модель прямого преобразования координат (u_a, u_b → u_α, u_β) приведена на рис. 7.

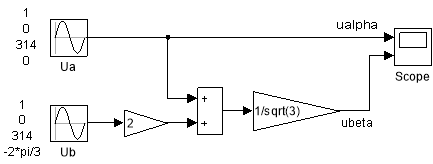
Рис. 7. Прямое преобразование координат u_a, u_b → u_α, u_β

Представим систему (4) в матричной форме:

	=	1	0	·

Схема прямого преобразования в виде матрицы в блоке Gain приведена на рис. 8. Задание матрицы в блоке Gain показано на рис. 9.

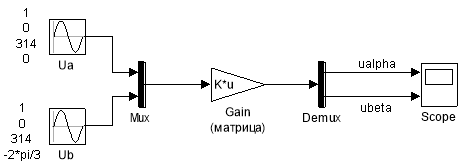
Рис. 8. Прямое преобразование координат u_a, u_b → u_α, u_β в виде матрицы в блоке Gain

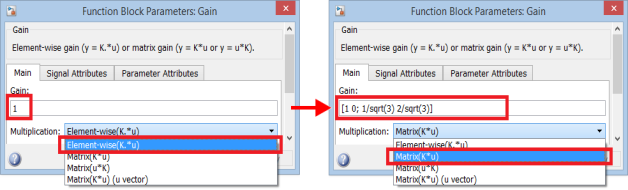
Рис. 9. Задание матрицы в блоке Gain

Результаты моделирования прямого преобразования координат даны на рис. 10.

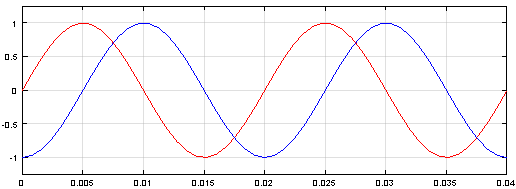
Рис. 10. Графики напряжений u_α и u_β

Б) Обратный перевод переменных из двухфазной системы в трехфазную: α, β → a, b, c.

Подставим u_α (u_a = u_α) во второе уравнение системы (4):

Отсюда выразим u_b, для чего умножим это уравнение на :

Система уравнений (4) преобразуется к виду:

(5)

В матричной форме:

	=	1	0	·

Математическая модель обратного преобразования координат (u_α, u_β → u_a, u_b, u_c) в матричной форме дана на рис. 11. Задание матрицы в блоке Gain показано на рис. 12.

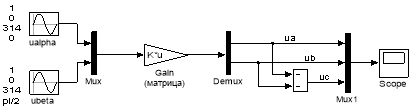
Рис. 11. Обратное преобразование координат u_α, u_β → u_a, u_b, u_c

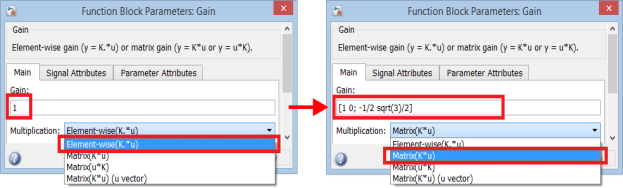
Рис. 12. Задание матрицы в блоке Gain

Результаты моделирования обратного преобразования координат даны на рис. 13.

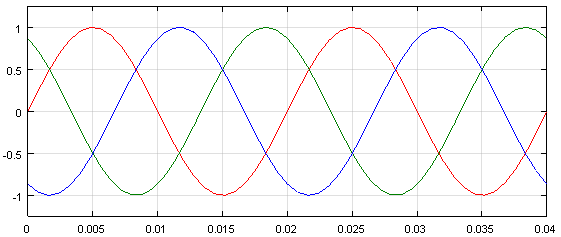
Рис. 13. Графики напряжений u_a, u_b и u_c

Литература:

1. Емельянов А.А., Бесклеткин В.В., Авдеев А.С., Чернов М.В., Киряков Г.А., Габзалилов Э.Ф., Прокопьев К.В. Математическое моделирование САР скорости системы «АИН ШИМ – АД» с переменными ψ_r – i_s на основе интегрирующих звеньев в Script-Simulink // Молодой ученый. — 2016. — №2. — С. 49-66.
2. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. – 654 с.
3. Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.