Построение параметризации походки робота-гексапода
Авторы: Желонкина Ольга Сергеевна, Злобин Данил Юрьевич
Рубрика: 1. Математика
Опубликовано в
международная научная конференция «Исследования молодых ученых» (Казань, июнь 2019)
Дата публикации: 03.06.2019
Статья просмотрена: 1270 раз
Библиографическое описание:
Желонкина, О. С. Построение параметризации походки робота-гексапода / О. С. Желонкина, Д. Ю. Злобин. — Текст : непосредственный // Исследования молодых ученых : материалы I Междунар. науч. конф. (г. Казань, июнь 2019 г.). — Казань : Молодой ученый, 2019. — С. 4-7. — URL: https://moluch.ru/conf/stud/archive/339/15162/ (дата обращения: 21.09.2024).
В данной работе строится кинематическая модель шестиногого робота, рассматривается обратная задача кинематики построенной модели. Затем решается задача генерации походки, в рамках которой находятся траектории движения ног гексапода.
Ключевые слова: робототехника, робот, гексапод, кинематика, кинематическая модель, прямая задача кинематики, обратная задача кинематики, походка, шаговый цикл.
Введение
Удобство применения роботов в работе породило большое их разнообразие. Существуют колесные и гусеничные роботы, летающие и шагающие. Так, например, шагающие роботы имеют большую проходимость на пересеченной местности, нежели колесные роботы [1]. Среди шагающих роботов шестиногий сочетает в себе устойчивость конструкции и простоту управления. Он может использоваться для работы в труднодоступных или малопригодных для человека местах, например осматривая завалы после катастроф или собирая образцы на других планетах.
Кинематика робота-гексапода
Объектом исследования является шестиногий шагающий робот с платформой в виде равностороннего шестиугольника, в углах которого располагаются трехзвенные конечности, состоящие из промежуточного звена, бедра и голени.
Введем две системы координат: систему координат платформы ![]() и систему координат конечности
и систему координат конечности ![]() . Центр первой из них расположен в центре платформы робота, плоскость
. Центр первой из них расположен в центре платформы робота, плоскость ![]() совпадает с плоскостью платформы, ось
совпадает с плоскостью платформы, ось ![]() направлена в точку прикрепления первой ноги, ось
направлена в точку прикрепления первой ноги, ось ![]() направлена вверх относительно земли перпендикулярно платформе (предполагаем, что робот не переворачивается). Центр второй из них расположен в точке прикрепления ноги, плоскость
направлена вверх относительно земли перпендикулярно платформе (предполагаем, что робот не переворачивается). Центр второй из них расположен в точке прикрепления ноги, плоскость ![]() также совпадает с плоскостью платформы, ось
также совпадает с плоскостью платформы, ось ![]() направлена от центра платформы к точке прикрепления ноги, ось
направлена от центра платформы к точке прикрепления ноги, ось ![]() направлена, как и
направлена, как и ![]() .
.
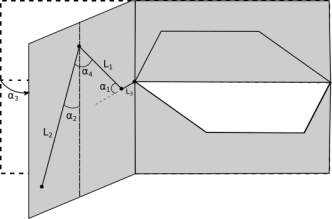
Рис. 1. Геометрическая модель ноги робота
Координаты стоп (оконечностей ноги) робота в системе координат конечности ![]() (углы показаны на рис. 1):
(углы показаны на рис. 1):
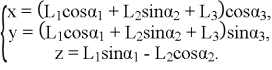 (1)
(1)
Решение обратной задачи кинематики
Мы получили выражение координат стопы через углы сочленений ноги, задачи подобного типа принято называть прямой задачей кинематики [3]. Далее естественно задаться вопросом о возможном обратном преобразовании координат стопы в углы ориентации, то есть провести решение обратной задачи кинематики. Используя геометрический метод [4], разрешим систему (1) относительно ![]() . В общем случае решение данной задачи не единственно, но выберем решение, которое соответствует верхнему расположению коленного сустава, как более естественное:
. В общем случае решение данной задачи не единственно, но выберем решение, которое соответствует верхнему расположению коленного сустава, как более естественное:
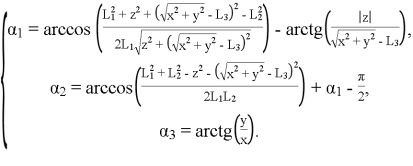 (2)
(2)
Последовательно вычисляя ![]() , найдем искомое решение системы.
, найдем искомое решение системы.
Параметризация походки
Для генерации походки разобьем конечности на две группы: с четными и нечетными номерами. В то время как одна группа ног располагается в воздухе, что соответствует фазе переноса, другая группа ног находится на земле, то есть в фазе опоры. Такая походка соответствует насекомым (например, муравьям и мухам), поэтому называется инсектовидной. Каждая фаза длится одинаковое время T. Разница фаз групп ног также составляет T. Рассмотрим шаговый цикл ноги гексапода. Траектория конечности в локальной системе координат представляет собой замкнутую кривую. Данную кривую можно условно разделить на две части, которые соответствуют фазе переноса ноги и фазе опоры ноги. При переносе конечности из одной точки в другую выбор траектории может быть осуществлен произвольным образом, так как стопа находится в свободном движении. В данной работе в качестве траектории переноса ноги используется полуэллипс. В фазе опоры нога движется по опорной поверхности вдоль прямой в направлении, обратном движению всего механизма.
Фаза переноса
Параметризация эллипса в системе координат конечности выглядит следующим образом:
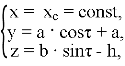
где:
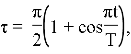
− ![]() — полупериод одного шага, то есть время, за которое происходит перестановка одной тройки ног,
— полупериод одного шага, то есть время, за которое происходит перестановка одной тройки ног,
− ![]() — расстояние от платформы гексапода до земли,
— расстояние от платформы гексапода до земли,
− ![]() и
и ![]() — большая и малая полуоси эллипса соответственно.
— большая и малая полуоси эллипса соответственно.
Зависимость параметра τ от времени принята на основе работы [5]. Такой ее вид обеспечивает постановку ноги на землю с нулевой конечной скоростью, что позволяет избежать ударов.
Идея организации походки заключается в том, что плоскость траектории движения каждой стопы ставится под таким же углом к оси ![]() (ось системы координат платформы робота), как и направление движения механизма к этой оси. Угол, необходимый для постановки i-ой ноги в нужном направлении, равен:
(ось системы координат платформы робота), как и направление движения механизма к этой оси. Угол, необходимый для постановки i-ой ноги в нужном направлении, равен:
![]()
где ![]() — угол между направлением движения гексапода и осью
— угол между направлением движения гексапода и осью ![]() .
.
Для постановки плоскости траектории стопы гексапода нужным образом, проведем следующие действия: параллельным переносом сдвинем эллипс в плоскость
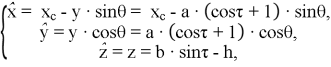 (3)
(3)
где ![]() .
.
Фаза опоры
Для нахождения части траектории, соответствующей фазе опоры ноги, соединим конечные точки эллипса. Уравнение соответствующей прямой можно записать в параметрическом виде:
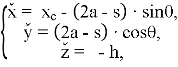 (4)
(4)
где ![]() .
.
Зависимость параметра от времени выбрана по аналогии с параметром τ, таким образом в граничных точках скорость обращается в ноль, следовательно, проскальзывание отсутствует.
Подставляя в систему уравнений (2) в качестве ![]() параметризации
параметризации ![]() из системы (3) и
из системы (3) и ![]() из системы (4), получим аналитический вид выражений углов в сочленениях гексапода от времени для фазы переноса и фазы опоры соответственно.
из системы (4), получим аналитический вид выражений углов в сочленениях гексапода от времени для фазы переноса и фазы опоры соответственно.
Заключение
Исследована кинематическая модель робота-гексапода, с помощью которой можно определить координаты стоп в зависимости от обобщенных координат. Решена обратная задача кинематики. В качестве походки выбрана походка, определяемая движением ног по тройкам (инсектовидная). Задана параметризация движения стопы в форме полуэллипса. Найдены соответствующие ей уравнения, которые позволяют осуществлять шаговый цикл в любом направлении
Литература:
- Potts, Alain & Jaime da Cruz, Jose. (2011). A Kinematical and Dynamical Analysis of a Quadruped Robot. DOI: 10.5772/25500.
- Ермолин В. С., Королев В. С., Потоцкая И. Ю. Теоретическая механика. Кинематика. СПб: ВВМ СПбГУ, 2012.
- John J. Craig. Introduction to Robotics: Mechanics and Control (3rd Edition). Pearson, 2004.
- Пименов В. Г., Ложников А. Б. Численные методы. Часть 2. Издательство Уральского университета, 2014.
- Павловский, В.Е., Панченко А. В. Модели и алгоритм управления движением малого шестиногого робота. Мехатроника, автоматизация, управление. — 2012. — № 11. — С.23 –28.
Ключевые слова
кинематическая модель, робототехника, робот, кинематика, прямая задача кинематики, гексапод, обратная задача кинематики, походка, шаговый циклПохожие статьи
Кинематическое управление шестиногим шагающим роботом
В данной работе строится кинематическая модель шестиногого робота, рассматривается обратная задача кинематики построенной модели в двух формах: аналитической и численной. Затем решается задача генерации походки в случае движения по ровной поверхности...
Решение обратной задачи динамики кинематических цепей
В данной работе рассматривается решение обратной задачи динамики кинематических цепей.
Ключевые слова: кинематические цепи, робототехника, обратная задача динамики, кинематика цепей, динамика цепей, тензорное исчисление, прямая задача кинематики.
Кинематическая модель космического манипуляционного робота
- Представлена реализация первой задачи кинематики для заданной модели космического робота в виде графического представления траекторий точек робота в абсолютной системе координат. Также проиллюстрирована зависимость угловых и линейных скоростей робота от...
Разработка технологии автоматизации процесса монтажа...
Решение обратных задач геометрии и кинематики (заданы траектория движения рабочей... Кинематическая модель космического манипуляционного робота. Приводится решение первой задачи кинематики манипулятора с использованием пакета расширения Symbolic Math...
Кинематика избыточного манипулятора робота для тушения...
Кинематическая модель. Одной из главных задач кинематики манипуляторов является определение положения полюсов робота и характеристической точки инструмента в инерциальной системе координат через обобщенные координаты.
Идентификация геометрических параметров роботов
Если обратная кинематическая задача решается с использованием обратной геометрической модели на основе значений параметров , то в модели
Ключевые слова: космическая робототехника, кинематическая модель, первая задача кинематики манипулятора.
Математическое моделирование движения плоского...
Выделим 4 отдельные фазы движения робота: I фаза: режим силового
Введем неподвижную систему координат с центром в точке А3, при этом ось А3Y направлена по линии
Задачей кинематического исследования является определение траектории перемещения, их скорости...
Кинематическое исследование гибкого планетарного механизма...
1. Проведена и составлена математическая модель кинематики движения сателлита-шпинделя гибкого эпи-гипоциклоидального планетарного механизма для рабочего органа привода шпинделей уборочного аппарата в рабочей и съемной зоне сбора хлопка-сырца.
Обзор и перспективы развития мобильных шагающих...
Кинематика робота сильно упрощена, так же как и система управления
Робот может работать в нескольких режимах: перемещение по координатам, следовании за лидером.
Двигательная система нового робота действует таким образом, что всегда три конечности...
Похожие статьи
Кинематическое управление шестиногим шагающим роботом
В данной работе строится кинематическая модель шестиногого робота, рассматривается обратная задача кинематики построенной модели в двух формах: аналитической и численной. Затем решается задача генерации походки в случае движения по ровной поверхности...
Решение обратной задачи динамики кинематических цепей
В данной работе рассматривается решение обратной задачи динамики кинематических цепей.
Ключевые слова: кинематические цепи, робототехника, обратная задача динамики, кинематика цепей, динамика цепей, тензорное исчисление, прямая задача кинематики.
Кинематическая модель космического манипуляционного робота
- Представлена реализация первой задачи кинематики для заданной модели космического робота в виде графического представления траекторий точек робота в абсолютной системе координат. Также проиллюстрирована зависимость угловых и линейных скоростей робота от...
Разработка технологии автоматизации процесса монтажа...
Решение обратных задач геометрии и кинематики (заданы траектория движения рабочей... Кинематическая модель космического манипуляционного робота. Приводится решение первой задачи кинематики манипулятора с использованием пакета расширения Symbolic Math...
Кинематика избыточного манипулятора робота для тушения...
Кинематическая модель. Одной из главных задач кинематики манипуляторов является определение положения полюсов робота и характеристической точки инструмента в инерциальной системе координат через обобщенные координаты.
Идентификация геометрических параметров роботов
Если обратная кинематическая задача решается с использованием обратной геометрической модели на основе значений параметров , то в модели
Ключевые слова: космическая робототехника, кинематическая модель, первая задача кинематики манипулятора.
Математическое моделирование движения плоского...
Выделим 4 отдельные фазы движения робота: I фаза: режим силового
Введем неподвижную систему координат с центром в точке А3, при этом ось А3Y направлена по линии
Задачей кинематического исследования является определение траектории перемещения, их скорости...
Кинематическое исследование гибкого планетарного механизма...
1. Проведена и составлена математическая модель кинематики движения сателлита-шпинделя гибкого эпи-гипоциклоидального планетарного механизма для рабочего органа привода шпинделей уборочного аппарата в рабочей и съемной зоне сбора хлопка-сырца.
Обзор и перспективы развития мобильных шагающих...
Кинематика робота сильно упрощена, так же как и система управления
Робот может работать в нескольких режимах: перемещение по координатам, следовании за лидером.
Двигательная система нового робота действует таким образом, что всегда три конечности...











