Введение.
В обыкновенной теории кооперативных игр принято, что игроки не ограничены в кооперации и могут образовывать коалиции с любыми игроками. Но в реальной жизни не всегда такое возможно. Чаще существуют какие-либо ограничения на кооперацию. Эти ограничения удобно представлять в виде графа, в котором вершины это игроки, а ребра отражают связи игроков, по которым они могут кооперировать. В этой статье рассмотрены некоторые решения кооперативных игр, которые распределяют общий выигрыш с учетом ограничений посредством графа. Существует множество таких решений, многие из них достаточно хорошо изучены, но в данной работе взяты за основу AT-решение [1] и на вектор Майерсона [2].
Кооперативная игра сограниченной кооперацией.
Обычная кооперативная игра — это игра нескольких лиц, у каждого из которых есть конечное множество стратегий и одна общая цель, как правило это всем вместе заработать как можно больше.
Итак, пусть N — непустое конечное множество игроков, N = {1, 2, …, n}. Любое объединение игроков (непустое подмножество S 
N) называется коалицией. Характеристической функцией называется такая функция v(S), если для любых непересекающихся коалиций T, S (T N, S N) выполняется:
v(T) + v(S) 
v(T 
S), v(
) = 0.
Характеристическая функция ставит в соответствие каждой коалиции суммарный выигрыш, который получат участники данной коалиции. Таким образом пара (N, v) есть кооперативная игра в форме характеристической функции.
Графом на N является множество ненаправленных пар различных членов множества N. Эти пары называются связями, и обозначаются {i, j} ({i, j} = {j, i}, так как связи не направлены). Пусть 
— полный граф:
.
Для 
граф 
называется подграфом, если = {{i, j} ∈ g | i, j ∈ K}. Последовательность из k различных узлов (
,..., 
) называется путем в графе , если {
,
}
для 
. Две вершины 
связаны в графе , если 
или существует путь 
с 
и 
. Граф связный, если любые два узла 
связаны в . Набор узлов K называется связным подмножеством N, когда подграф связан. Подмножество K из N является компонентом g, если подграф максимально связен, т. е. связен для любой j, а подграф 
несвязный. Набор всех компонент обозначается через 
. Можно сказать, что это набор маленьких коалиций, на которые распадается K, если игроки взаимодействуют только по связям, образованным графом g. Однако, если два игрока не имеют связи друг с другом, они могут состоять в одной коалиции, если между ними есть путь в графе коопераций. Компоненту, которая содержит игрока 
будем обозначать 
.
Тройка (N, v, g) называется кооперативная игра с ограниченной кооперацией. Решением такой игры является правило, которое каждой игре ставит в соответствие дележ. Дележом максимального выигрыша называется такой вектор
= (
, …, 
), удовлетворяющий:
v({i}), i 
N
= v(N),
где 
— сумма, которую получит игрок i.
Вектор Майерсона.
Введем вектор Майерсона, следуя [3], для этого необходимо определить вспомогательную характеристическую функцию 
, зависящую от графа g:
∀S ⊂ N, (S) = 
v(T).
Согласно [2], вектор Майерсона это правило Y: (N, v, g) 
, которое каждой игре с ограниченной кооперацией ставит в соответствие вектор распределения 
(g) = ((g), …, (g)). Таким образом 
(g) — выигрыш, который получит игрок i если g является структурой соглашения между игроками. И этот выигрыш равен
[v,g] = 
[(T) − (T\{i})],
где |T| = t, |N| = n.
AT-решение.
Теперь определим AT-решение, согласно работе [4].
Если ненаправленный граф — дерево с корнем h, то для него определим направленный граф T(h), в котором все ребра направлены от тех узлов, которые находятся ближе к корню h. Направленные ребря будем обозначать (i, j). Если (i, j) 
, то узел j является преемникомi, а i является предшественником j. Будем называть j 
i подчиненным i, если существует направленный путь из i в j. Обозначим множество подчиненных i в T(h) через 
и обозначим
= 
{i}. Примем, что 
— это множество преемников i в дереве T(h), т. е. {i | (j, i) T(h)}. Поэтому 
.
AT-решение Z [v, g] = (
[v, g],..., 
[v, g]) в кооперативной игре с коммуникационной структурой было введено в [1] для случая графов без циклов, и оно задается по следующему правилу:
i
,
где 
.
Можно сказать, что выигрыш игрока равен среднему среди всех 
— вкладов игрока i в дерево от игрока j. Этот вклад в свою очередь равен ценности коалиции, состоящей из игрока i и всех его подчиненных в T(j) за вычетом суммарной ценности коалиций, состоящих из любых преемников игрока i и всех подчиненных этого преемника в T(j).
Пример.
Пусть N = {1, 2, 3, 4}, характеристическая функция определена как:
v(1) = v(2) = v(3) = v(4) = 0,
v(1, 2) = v(1, 3) = v(1, 4) = v(2, 3) = v(2, 4) = v(3, 4) = 10,
v(1, 2, 3) = v(1, 2, 4) = v(1, 3, 4) = v(2, 3, 4) = 30, v(N) = 100.
И пусть есть два графа
и 
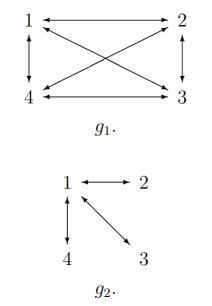
Первый граф представляет собой коалицию каждого с каждым. Поэтому и вектор Майерсона этого графа равен AT-решению:
Y [v,] = 
[v,] = (25; 25; 25; 25).
Второй же гарф интересней. Особенность в том, что 2, 3 и 4 игроки не могут кооперироваться друг с другом, все коалиции в этой игре проходят через первого игрока. Следовательно, у первого игрока наибольший вклад и наибольшая доля. Согласно вектору Майерсона выигрыши игроков равны:
Y [v,] = (35; 21,(6); 21,(6); 21,(6)),
распределение, построенное согласно AT-решению имеет вид:
Z [v,] = (77,5; 7,5; 7,5; 7,5).
Не трудно заметить, что при одинаковых условиях решения дают разные ответы. Следовательно, для разных задач можно подобрать разные подходы к поиску решения.
Выводы.
В данной статье рассматривается модель игры, в которой есть ограничения на кооперацию, эти ограничения можно представить как ненаправленный граф, где вершины — это игроки, а ребра это связи между игроками. Соответственно игроки могут взаимодействовать, только если между ними существует эта самая связь. Для этой модели рассмотрены два наиболее известных решения и проведен их сравнительный анализ.
Литература:
- Herings P. J. J., Van der Laan G., Talman D., The average tree solution for cycle-free graph games // Games and economic behavior. 2008. NO 62. P. 77–92
- Roger B. Myerson. Graphs and cooperation in games. mathematics of operations research. Vol. 2. No. 3, August 1977.
- Козлов А. Д., Сорокин В. А. Принципы оптимальности распределения выигрыша в задачах теории кооперативных игр // Almanahul SWorld. 2019. № 1. C. 35–40.
- Козлов А. Д., Сорокин В. А. Пример решения игры с иерархической схемой // Процессы управления и устойчивость. 2019. № 1. T. 6. С. 466–470.
- Петросян Л. А., Зенкевич Н. А., Шевкопляс Е. В. Теория игр. СПб.: БXB-Петербург, 2012.
