Моделирование САР скорости асинхронного двигателя с переменными is – ψr в системе относительных единиц в Matlab и Си



В данной статье покажем поэтапное преобразование всех элементов САР скорости из Matlab-Simulink в Matlab-Script и Си. На рис. 1 приводим всю систему, в которой даны модель асинхронного двигателя (номер 7), в контурах тока по проекциям x и y соответствующие ПИ-регуляторы тока (номера 4 и 6), в контуре скорости П-регулятор скорости (номер 1).

Важным элементом является контур потока с ПИ-регулятором потока (номер 2). Для ориентации системы координат по потокосцеплению ротора вводится наблюдатель (номер 8). В модели учтена компенсация перекрестных связей (номер 5). Сигнал задания по скорости выполнен на задатчике интенсивности. В цепи задания скорости перед регулятором скорости предусмотрен фильтр.

Алгоритм перевода всех элементов САР скорости:

− приводится математическая формула той или иной переменной, выраженной в Simulink;

− приводится его структурная схема;

− переход от изображений к оригиналу (от s к d/dt) и решение с помощью простого метода Эйлера.

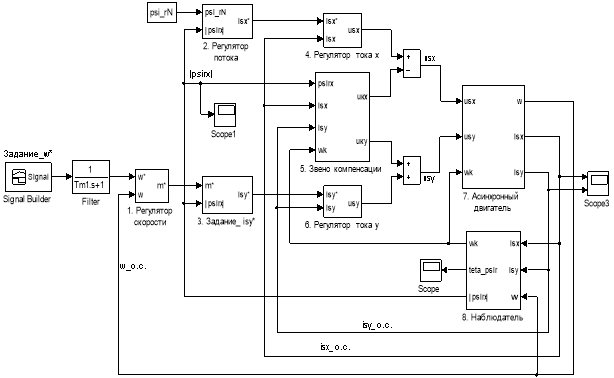
Рис. 1. Математическая модель САР скорости асинхронного двигателя

Математическая модель асинхронного двигателя с переменными i_s – ψ_r в Matlab и Си дана в статье [1].

Математическое моделирование регуляторов тока

Matlab-Simulink:

Передаточная функция для регуляторов тока по проекциям x и y:

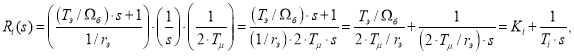
гдеT_μ - некомпенсируемая постоянная времени (примем T_μ = 0,0025 с);

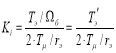- коэффициент пропорциональной части регулятора тока;

- постоянная времени интегральной части регулятора тока.

Математические модели ПИ-регуляторов тока по проекциям x и y в Simulink приведены на рис. 2.

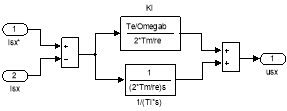
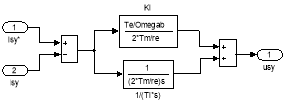
Рис. 2. ПИ-регуляторы тока по проекциям x и y в Simulink

Matlab-Script:

Пропорциональная часть регулятора тока по оси x в Simulink:

Выразим пропорциональную часть в Matlab-Script:

где

Интегральная часть регулятора тока по оси x в Simulink:

Переходим от изображения к оригиналу:

Выразим интегральную часть через конечные разности:

Уравнение напряжения задания u_sx^* на выходе регулятора тока по оси x:

Аналогично преобразуем регулятор тока по оси y в Matlab-Script.

Пропорциональная часть:

Интегральная часть:

Уравнение u_sy^* на выходе регулятора тока по оси y:

Си:

Исключив (i) и (i+1), получим уравнения регуляторов тока на языке Си:

Моделирование наблюдателя потокосцепления ротора

Модель наблюдателя потокосцепления ротора в Simulink приведена на рис. 3. Преобразуем эту модель в Matlab-Script.

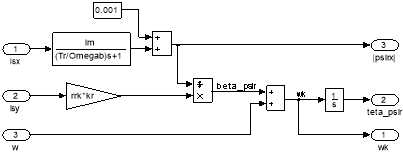
Рис. 3. Модель наблюдателя потокосцепления ротора в Simulink

Приведем уравнение модуля потокосцепления ротора к оригиналу:

Переходим к конечным разностям:

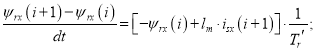
Уравнение скольжения β_ψr для программирования в Matlab-Script:

Отсюда угловая скорость вращения системы координат:

Уравнения наблюдателя потокосцепления ротора на Си будут иметь вид:

Математическое моделирование регулятора потока

Модель ПИ-регулятора потока в Simulink дана на рис. 4.

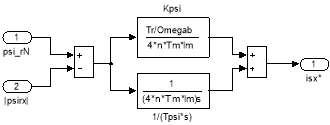
Рис. 4. ПИ-регулятор потока в Simulink

Номинальное потокосцепление ротора определяется по следующей формуле и при векторном управлении поддерживается постоянным [3]:

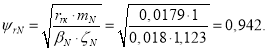
Передаточная функция регулятора потока:

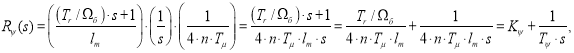
гдеn = 2;

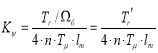- коэффициент пропорциональной части регулятора потока;

- постоянная времени интегральной части регулятора потока.

Определим пропорциональную часть в Matlab-Script:

где

Интегральная часть регулятора потока:

Переходим от изображения к оригиналу:

Выразим интегральную часть через конечные разности:

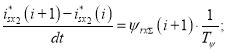
Определим задание тока i_sx^* на выходе регулятора потока в Matlab-Script:

Отсюда уравнения регулятора потока для программирования на Си:

Математическое моделирование регулятора скорости

Пропорциональный регулятор скорости в Simulink приведен на рис. 5.

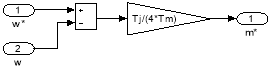
Рис. 5. Пропорциональный регулятор скорости в Simulink

Передаточная функция регулятора скорости:

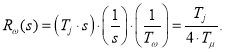
Определим задание момента m^* в Matlab-Script:

где

Преобразуем эти уравнения для программирования на Си:

Математическое моделирование компенсации перекрестных связей

Математическая модель компенсации перекрестных связей в Simulink дана на рис. 6.

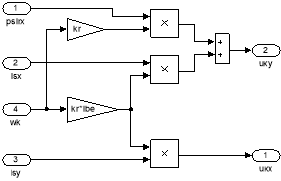
Рис. 6. Компенсация внутренних перекрестных связей в Simulink

Компенсационные составляющие каналов управления в Matlab-Script определятся следующим образом:

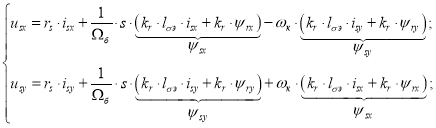
Уравнения компенсации перекрестных связей для Си:

Математическое моделирование задатчика интенсивности

Задание на скорость ω^* в Simulink формируется в блоке Signal Builder (рис. 7).

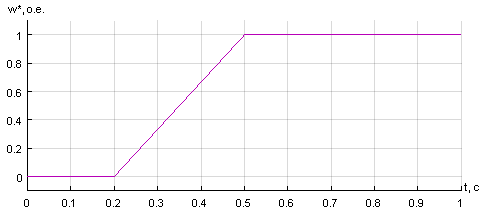
Рис. 7. Сигнал задания на скорость ω^* в Simulink

Программирование задания на скорость в Matlab-Script дано на рис. 8.

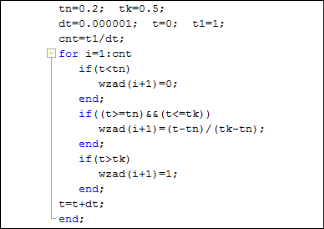
Рис. 8. Программирование задания на скорость в Matlab-Script

Моделирование задания скорости на выходе фильтра

Передаточная функция фильтра:

Определим задание скорости ω₁^* на выходе фильтра:

Перейдем от изображения к оригиналу:

Переходим к конечным разностям:

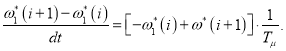
Задание скорости ω₁^* на выходе фильтра в Matlab-Script будет иметь вид:

Преобразуем это уравнение для программирования на Си:

Моделирование задания статорного тока по проекции y

Математическая модель задания токаi_sy^* в Simulink дана на рис. 9.

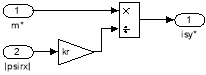
Рис. 9. Реализация задания статорного тока i_sy^* в Simulink

Задание токаi_sy^* в Matlab-Script:

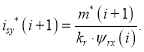
Задание токаi_sy^* на Си:

Результаты моделирования САР скорости асинхронного двигателя в Simulink приведены на рис. 10.

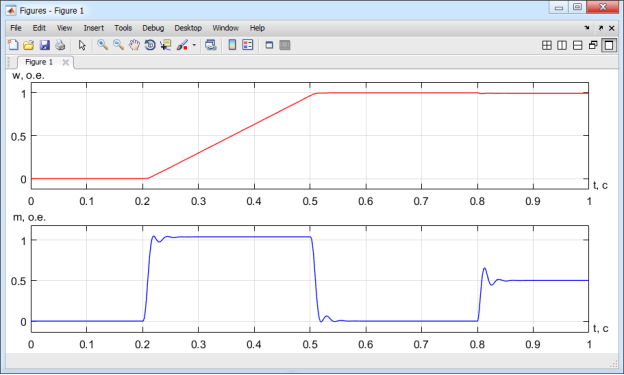
Рис. 10. Графики скорости и электромагнитного момента в Simulink

Математическая модель САР скорости асинхронного двигателя в Matlab-Script приведена на рис. 11 и 12. Результаты моделирования в Matlab-Script приведены на рис. 13.

Программирование САР скорости асинхронного двигателя на языке Си представлено на рис. 14 и 15.

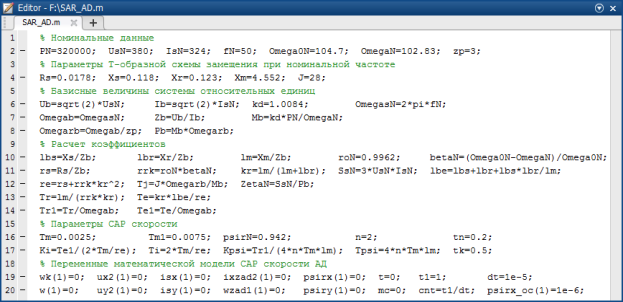
Рис. 11. Параметры САР скорости асинхронного двигателя в Matlab-Script

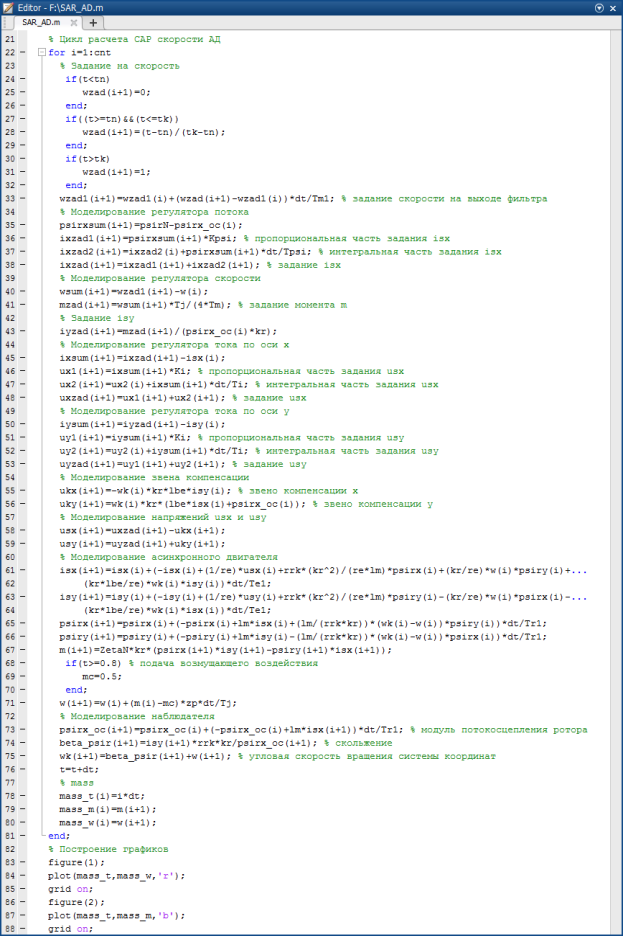
Рис. 12. Цикл расчета САР скорости асинхронного двигателя в Matlab-Script

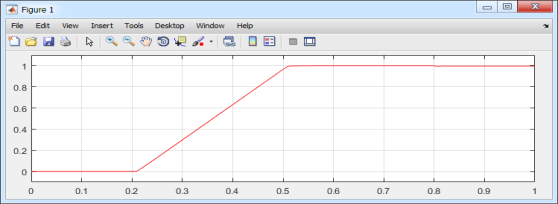
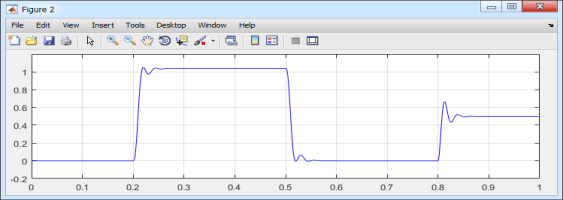
Рис. 13. Графики скорости и электромагнитного момента в Matlab-Script

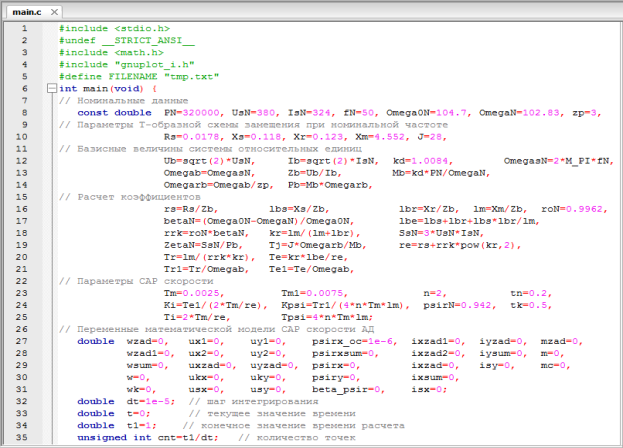
Рис. 14. Параметры САР скорости асинхронного двигателя на языке Си

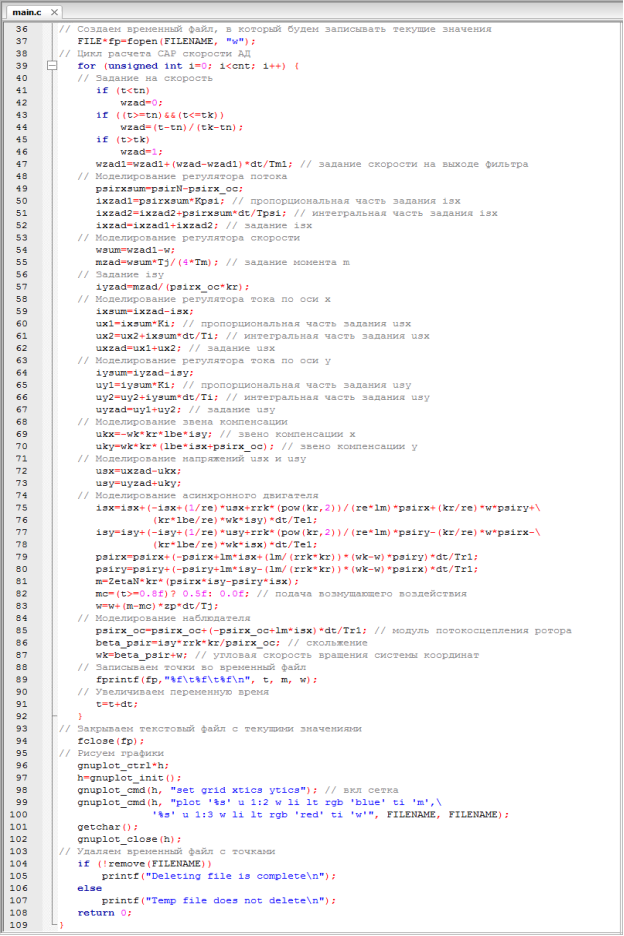
Рис. 15. Цикл расчета САР скорости асинхронного двигателя на языке Си

Результаты моделирования САР скорости асинхронного двигателя на языке Си приведены на рис. 16.

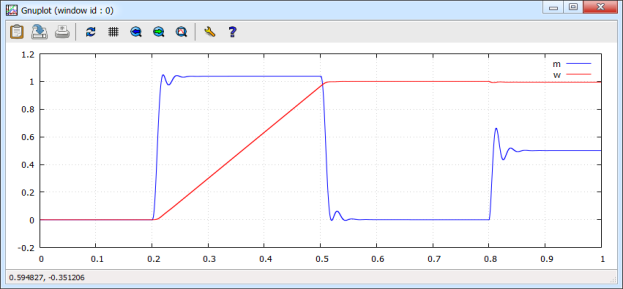
Рис. 16. Графики скорости и электромагнитного момента при моделировании на языке Си

Литература:

1. Емельянов А.А., Бесклеткин В.В., Зорин Д.И., Дятлов О.А., Бухряков И.Ф., Зозулин М.С., Онищенко К.Ю., Блинов Е.К., Пестеров Д.И. Моделирование асинхронного двигателя с переменными is - ψr в системе относительных единиц в Matlab и Си // Молодой ученый. - 2019. - №12. - С. 1-12.
2. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. - Екатеринбург: УРО РАН, 2000. - 654 с.
3. Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.
4. Васильев А.Н. Программирование на C++ в примерах и задачах. – М.: Издательство «Э», 2017. – 368 с.