Построение графиков функций изучаемых величин способствует более полному пониманию процесса, рассматриваемого в задаче. В ряде случаев такие графики открывают новый взгляд на изучаемый процесс и являются весьма полезным инструментом решения поставленной задачи. Однако графические построения не всегда оказываются легко выполняемыми, особенно если в решении задачи используются дифференциальные уравнения, описывающие динамику некоторого процесса.
В статье на примере типовой задачи анализируются особенности аналитических расчётов и построения на их основе графиков рассматриваемых зависимостей в программе Microsoft Excel.
Ключевые слова: построение графиков функций, графические построения, электронной таблицы Excel.
The construction of graphs of the functions of the quantities studied contributes to a more complete understanding of the process considered in the problem. In a number of cases, such graphs open a new look at the process under study and are a very useful tool for solving the task. However, graphical constructions do not always turn out to be easily executed, especially if the solution of the problem uses differential equations describing the dynamics of a certain process.
In the article, the features of analytical calculations were analyzed with the example of a typical problem. Also the graphs of the dependencies were constructed in the program Microsoft Excel.
Keywords: Construction of graphs of functions, graphical constructions, Excel spreadsheet.
Введение.
Построение графиков функций изучаемых величин способствует более полному пониманию процесса, рассматриваемого в задаче. В ряде случаев такие графики открывают новый взгляд на изучаемый процесс и являются весьма полезным инструментом решения поставленной задачи. Однако графические построения не всегда оказываются легко выполняемыми, особенно если в решении задачи используются дифференциальные уравнения, описывающие динамику некоторого процесса. В настоящее время сложности численных расчетов при построении графиков функций можно решить использованием компьютерных программ, которые могут выполнять графические построения широкого класса функций. Одной из таких программ является программа электронной таблицы Microsoft Excel 2010 [1]. Электронная таблица весьма удобна для проведения несложных численных расчетов. Программа имеет простой интерфейс, позволяющий решать математические задачи с минимальным количеством арифметических ошибок в расчетах и графические средства для представления результатов в виде графиков и диаграмм. Студенты младших курсов, как правило, достаточно хорошо владеют компьютерными программами семейства Microsoft Office, поскольку они изучаются в школьном курсе информатики и студенты первого курса могут использовать электронную таблицу при выполнении домашнего задания по курсу общей физике. Опыт применения электронной таблицы Excel в решении задачи на затухающие механические колебания представлен в [2].
На примере задачи, похожей на типовую задачу, предлагаемую студентам второго курса МГТУ им. Н. Э. Баумана, изучающим тему «Электромагнитная индукция» в качестве домашнего задания [3, 4], рассмотрим возможность применения электронной таблицы. В задаче исходные данные представлены в общем виде, как алгебраические соотношения, меняющиеся в зависимости от варианта задания, в нашем случае будем использовать следующие исходные данные: ![]() ,
, ![]() .
.
Задача. По двум главным медным шинам скользит перемычка массы M, закон движения которой задан ![]() .Сопротивление перемычки равно R0. Сверху шины замкнуты электрической цепью, состоящей из индуктивности L. Расстояние между шинами l. Система находится в однородном переменном магнитном поле с индукцией
.Сопротивление перемычки равно R0. Сверху шины замкнуты электрической цепью, состоящей из индуктивности L. Расстояние между шинами l. Система находится в однородном переменном магнитном поле с индукцией![]() , перпендикулярной плоскости, в которой перемещается перемычка. Сопротивлением шин, скользящих контактов можно пренебречь. В начальный момент времени ток через индуктивность отсутствует.
, перпендикулярной плоскости, в которой перемещается перемычка. Сопротивлением шин, скользящих контактов можно пренебречь. В начальный момент времени ток через индуктивность отсутствует.
В задаче требуется найти следующие зависимости: ЭДС индукции и самоиндукции от времени, силу тока I(t), а также зависимость скорости и ускорения перемычки от времени, силу Ампера Fa(t) и силу F(t), действующую на перемычку, необходимую для обеспечения заданного закона движения и построить графики найденных зависимостей.
Вначале задача должна решаться аналитическим способом с выводом всех формул, определяющих искомые величины. Программа Excel является лишь средством для выполнения расчетов и построения графиков функций, и поэтому электронная таблица используется после того, как получены аналитические решения. Один из возможных вариантов решения задачи домашнего задания заключается в следующем:
Для решения представленной задачи необходимо составить уравнение второго закона Кирхгофа с учетом явления электромагнитной индукции и уравнение второго закона динамики Ньютона. Из уравнения второго закона Кирхгофа получаем линейное дифференциальное уравнение с постоянными коэффициентами, которое решаем методом
Лагранжа и находим зависимость изменения тока I(t) в виде:
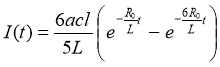
Теперь можно найти силу Ампера, действующую на перемычку:
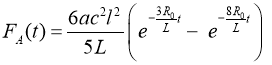
Далее, из уравнения второго закона динамики Ньютона находим зависимость проекции управляющей силы F(t) на ось Оу, действующую на перемычку, в виде:
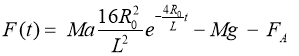
Каждая из полученных ранее зависимостей может быть отображена в виде графика с помощью электронной таблицы. Для этого надо запрограммировать формулу в виде команд электронной таблицы, что не представляет труда, хотя надо иметь представление об абсолютных и относительных адресах ячеек таблицы. Например, зависимость управляющей силы от времени представляется в виде следующей формулы:
=$B$13*$B$1*(16*$B$3*$B$3/($B$4*$B$4))*EXP((-4*$B$3/$B$4)*C2)-$B$13*9,8-((6/5)*$B$1*$B$7*$B$7*$B$11*$B$11/$B$4)*(EXP((-3*$B$3/$B$4)*C2)-EXP(
(-8*$B$3/$B$4)*C2))
Отметим, что электронная таблица обладает встроенными средствами контроля ввода формул, что позволяет уменьшить количество опечаток. Если в какой-либо ячейке столбца запись формулы отличается от записи этой формулы в других ячейках этого же столбца, то данная ячейка помечается значком в виде треугольника и выводится предупреждающее сообщение: «Формула в этой ячейке отличается от других формул в этой области таблицы».
Заполнив электронную таблицу формулами, можно выполнить исследование поведения системы, изменяя коэффициенты в расчетных формулах. Однако, такое моделирование возможно лишь в пределах выбранных типов зависимостей. Например, если движение перемычки запрограммировано в виде экспоненциальной зависимости, то перейти к линейной зависимости нельзя, поскольку все формулы были получены аналитическим образом исходя из начальной экспоненциальной зависимости. Для решения задачи с новым типом зависимости потребуется и новая форма электронной таблицы. Тем не менее, даже не меняя типа полученных зависимостей, можно ответить на ряд вопросов и достаточно полно исследовать поведение системы. Например, как изменится сила Ампера, если скорость движения перемычки и ее масса увеличится вдвое? Что произойдет, если изменение магнитной индукции стороннего поля замедлится в сто раз? Или, например, какие изменения произойдут в системе, если поменять направление вектора магнитной индукции на обратное.
Воспользуемся графическими возможностями электронной таблицы и построим графики функций по аналитическим решениям задачи. В результате получим динамику изменения изучаемых величин от времени. На рисунке 1 представлены зависимости электромагнитных характеристик системы от времени: ЭДС индукции контура, ЭДС самоиндукции катушки индуктивности, а также результирующая ЭДС и ток в контуре. Из рисунка видно, что ЭДС индукции контура и ЭДС самоиндукции катушки индуктивности имеют разные знаки, что отвечает правилу Ленца, при этом результирующая ЭДС все время убывает, а ток в контуре в течение некоторого промежутка времени возрастает и достигает максимального значения, убывает экспоненциально.
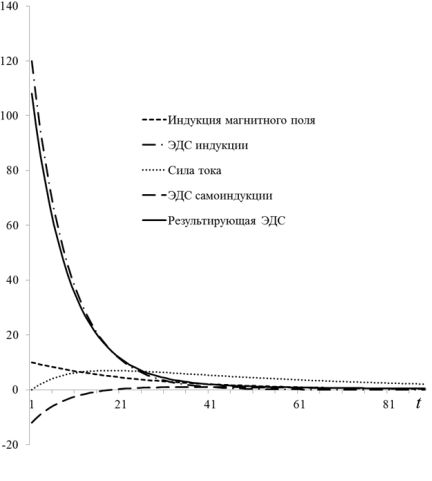
Рис. 1. Зависимость электромагнитных характеристик системы от времени: индукция магнитного поля (1), ЭДС индукции контура (2), сила тока в контуре (3), ЭДС самоиндукции катушки индуктивности (4), результирующая ЭДС в контуре (5)
На рисунке 2 представлены зависимости механических характеристик системы от времени: проекции скорости и ускорения перекладины на ось Оу, сила Ампера, проекция управляющей силы на ось Оу и сумма проекций сил, действующих на перемычку. Как видно из рисунка, в выбраной системе координат проекция скорости перемычки отрицальна, а проекция ускорения положительна.
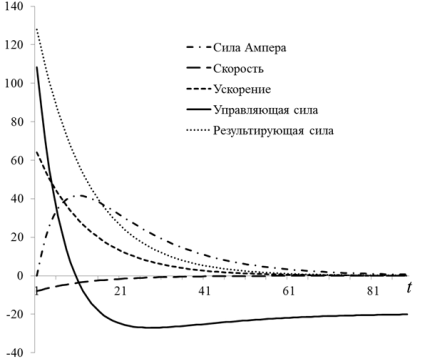
Рис. 2. Зависимость механических характеристик системы от времени: сила Ампера (1), проекция скорости (2) и ускорения (3) перемычки на ось Оу, проекция управляющей силы (ряд 4) на ось Оу, проекция результирующей силы, действующей на перемычку (5) на ось Оу
Проекция силы Ампера положительна и возрастает в течение некоторого отрезка времени, достигая максимального значения, а затем экспоненциально убывает. Чтобы обеспечить заданное в задаче изменение координаты, управляющая сила должна изменяется определенным образом. В начале движения проекция управляющей силы на ось координат Оу положительна, что соотвествуют силе, тормозящей движение перемычки. Затем знак проекции изменяется и сила из тормозящей становится движущей. Далее управляющая сила экспоненциально стремится к силе тяжести, при этом продолжает играть роль силы, удерживающей перемычку от падения. Сумма проекций двух сил, действующих на перемычку, также изменяется по экпоненциальной зависимости и определяет изменение ускорения перемычки.
Рассмотренная задача показывает, что построенные в электронные таблицы зависимости, отображаемые на графиках, описывают поведение системы достаточно наглядно. Однако имеется особенность использования программы Excel при изучении динамики процессов. Для удобства сравнения полученных величин желательно использовать одинаковые временные промежутки с одинаковым интервалом дискретизации времени при построении графиков функций изучаемых процессов.
Отметим, что для построения графиков функций использовалась программа Microsoft Excel 2010. Построение диаграмм выполнено в два этапа. Вначале по полученным численным данным с использованием стандартных макетов создавалась предварительная диаграмма. Далее выполнялась настройка диаграммы с изменением вида отдельных элементов диаграммы. При этом подбирался наиболее качественный вид отображения графиков. В результате настройки были изменены легенда диаграммы, линия сетки, цвет, толщина и вид линий графиков, выполнена настройка осей диаграммы.
Опишем последовательность команд, позволяющую выполнить настройку диаграмм. По умолчанию программа Excel использует в легенде имена «Ряд1, Ряд2, …» и т. д. Чтобы дать рядам данных осмысленные имена, отражающие суть дела, использовалась команда: Работа с диаграммами => Конструктор => Данные => Выбрать данные. Далее в открывшемся окне «Выбор источника данных» выделялся ряд данных, которому присваивается новое имя. После щелчка по кнопке «Изменить» в окне «Элементы легенды (ряды)» выполним переход к открывшемуся диалоговому окну «Изменение ряда». Затем в поле «Имя ряда» вводим новое имя, например, «Сила Ампера». Далее подтверждаем выполненные действия, дважды нажав на кнопку ОК.
Линия сетки в нашем случае загромождает диаграмму, отображающую несколько графиков функций, поэтому сетку отключали следующей командой: Работа с диаграммами => Макет => Оси => Сетка. В результате открывался список, в котором указаны все оси, представленные на диаграмме. Далее выбиралась команда «Не показывать горизонтальные линии сетки».
В электронной таблице можно выполнить настройку осей диаграммы. Это желательно сделать, чтобы ось категорий отображала временную шкалу не в условных градациях (1,2,3…), а в секундах. Для этого используем контекстное меню с командой «Выбрать данные». Затем в окне «Выбор источника данных» нажимается кнопка «Изменить» для «Подписи горизонтальной оси». Далее в открывшемся окне «Подписи оси» надо выбрать диапазон данных, с помощью указателя мыши выделяя столбец с данными «Время в секундах». Таким образом, получалась горизонтальная ось с градациями 0, 0,25, 0,5, 0,75, 1,1,25 с.
Чтобы изменить цвет и тип линий графика использовались команды группы ленты: Работа с диаграммами => Формат => Стили фигур. В диалоговом окне «Формат ряда данных» выбиралась вкладка «Цвет линии» и затем из палитры цветов выбирался черный цвет, а на вкладке «Тип линии» устанавливалась ширина линии в 1,5 пунктов и тип линии, например, пунктирный. Также на вкладке «Тип линии» устанавливался флажок «Сглаженная линия».
Заключение.
Использование электронной таблицы Microsoft Excel 2010 позволяет решить и исследовать решение домашних задач по физике без арифметических ошибок в расчетах и получить наглядные графики функций искомых величин. Для придания диаграммам профессионального вида не использовалось предопределенных макетов и стилей диаграмм, а был разработан собственный стиль, ориентированный на построение графиков в научных публикациях. Программа Excel позволяет применять дополнительное форматирование к отдельным элементам диаграмм, отображая результат в наиболее удобной и простой форме. В работе был рассмотрен простой способ применения электронной таблицы Excel без программирования с помощью VBA. Используя макросы, можно создавать программы моделирования протекания физических процессов в изучаемых системах с более широкими возможностями исследования, чем рассмотрены выше, например, можно варьировать начальными условиями и типом зависимостей и отображать результаты расчетов графиками функций.
Литература:
- Уокенбах Д. Microsoft Excel 2010. Библия пользователя. М.: ООО «И. Д. Вильямс», 2014, 912 с.
- Заблоцкий В. Р. Решение задачи домашнего задания по физике на затухающие механические колебания с помощью программы EXCEL. Труды восьмой Всероссийской конференции «Необратимые процессы в природе и технике» 27–29 января 2015 г. М.: МГТУ им. Н. Э. Баумана 2015, с.140–143.
- Лунева Л. А., Тараненко С. Н., Козырев А. В., Голубев В. Г., Купавцев А. В., под редакцией Макарова А. М. Электростатика. Магнитостатика. Электромагнитная индукция: методические указания к выполнению домашнего задания по курсу общей физики, М.: Изд-во. МГТУ им.Н. Э. Баумана, 2011, 55 с.
- Иродов И. Е. Электромагнетизм. Основные законы, М.: Лаборатория Базовых Знаний, 2000, 352 с.

