Целью статьи является ознакомление с разработанной имитационной моделью алгоритма Гровера в прикладной программе MATLAB, а также с результатами его работы, которые представлены в виде вычислений и графиков. Коротко описаны основы квантовых вычислений и подробно разобрана методика моделирования.
Ключевые слова: квантовый компьютер, кубит, квантовый алгоритм, алгоритм Гровера.
За последние десятилетия область квантовых вычислений стала активным полем исследований для тысячи ученых по всему миру. После важных открытий в области теории квантовых вычислений, достижений в экспериментальной физике и инженерии сделали возможным создание первого прототипа квантового компьютера. Несмотря на уже существующую коммерческие модели квантового компьютера, — IBM Q System One и D-Wave Systems, он по-прежнему остаётся труднодоступным для рядового исследователя в силу высокой цены и требовательных массогабаритных характеристик. Этим объясняется востребованность имитационных моделей, с помощью которых стало возможным на классических компьютерах как разрабатывать и изучать квантовые алгоритмы, так и симулировать их работу.
В 1965 году, один из основателей Intel Гордон Мур нашел закономерность: количество транзисторов, размещаемых на кристалле ИС, удваивается каждые 2 года (рисунок 1). Однако у этого роста есть предел. В 2007 году Мур заявил, что закон скоро перестанет действовать из-за ограничения скорости света и атомарной природы вещества. Таким образом, законы функционирования интегральных схем на столь малых базовых элементах должны определяться законами микромира или квантовой механики.
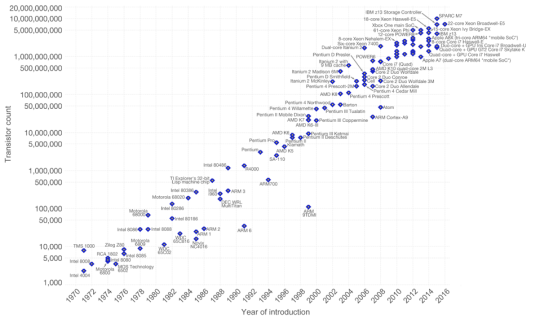
Рис. 1. Закон Мура — количество транзисторов на ИС с 1971 года по 2016
Применение квантовых компьютеров позволит реализовать новые алгоритмы, которые позволят решать задачи, требующие чрезмерно больших ресурсов при использовании классического компьютера. Этим объясняется и заинтересованность в развитии квантовых технологий не только таких технологических гигантов как IBM, Google, Microsoft, Intel, а также ведущих стран Великобритании, Германии, Израиле, Канаде, Китае, Нидерландах, России, США, Франции, Японии. Так, государственные программы финансирования квантовых разработок в Евросоюзе собрали €1 млрд (программа “Квантовый флагман”), в Великобритании — $400 млн, в США — $360 млн., в Китае — $220 млн.
В России исследования по этому направлению ведут специалисты Физико-технического института РАН (ФТИАН) во главе с академиков РАН К. А. Валиевым. Ректор МГУ Виктор Садовничий, который выпустил сборник переводов статей и журнал на тему исследования квантовых вычислений, а также две важные лекции Р. Фейнмана. Из российских теоретиков нельзя не упомянуть Александра Холево (автора выполненных еще в 1970-е годы пионерских работ по квантовой теории информации), Юрия Манина (первым в мире поставил в 1979 году проблему исследования вычислительного потенциала квантовых автоматов), Алексея Китаева. Российский квантовый центр при поддержке НИТУ «МИСиС» открыл Первую школу по квантовым коммуникациям в Образовательном центре «Сириус». В 2019 году был подписан договор с МФТИ о создании базовой кафедры вуза в RQC.
Рис. 2. Квантовая вычислительная машина фирмы D-Wave
В начале 2013 года в Канаде построена квантовая вычислительная машина фирмой D-Wave (рисунок 2), которая состоит из 512-кубитов на сверхпроводящих кольцах. В декабре 2015 года специалисты компании Google подтвердили, что компьютер D-Wave использует квантовые эффекты. При этом в «1000-кубитном» компьютере кубиты организованы в кластеры по 8 кубит каждый. Тем не менее, это позволило добиться быстродействия в 100 млн раз больше (по сравнению с обычным компьютером) в одном из алгоритмов. С 2018 года компания разрабатывает 4000-кубитную машину, где кубиты организованы в кластеры по 16 кубит каждый. На сегодняшний день квантовую вычислительную машину фирмы D-Wave приобрела компания Lockheed Martin для исследования возможностей использования в оборонных заказах, а также компания Google для проектирования систем искусственного интеллекта, способного к самообучению.
Квантовый компьютер исследуют для применения в криптографии и для взлома шифров. Данным вопросом заинтересованы оборонные ведомства, которые финансируют работы Стэнфордского университета (США) по созданию квантового компьютера.
В национальном исследовательском технологическом университете (НИТУ «МИСиС») работает первая в России лаборатория, которая стала выполнять измерения кубитов при сверхнизких температурах (рисунок 3).
Рис. 3. Экспериментальная вычислительная машина в НИТУ «МИСиС»
Первый кубит, который измерили в 2013 году, был изготовлен в Германии, в лаборатории профессора Евгения Ильичева в Институте фотонных технологий (Institute of Photonic Technology). В Московском физико-техническом институте (МФТИ) появилась группа под руководством профессора Олега Астафьева, где исследуется система электронной литографии.
Российский квантовый центр, МФТИ, НИТУ МИСиС, Института физики твердого тела РАН объединились в коллаборацию для создания первого образца работающего сверхпроводящего кубита. Были подписаны соглашения о совместных действиях по развитию квантовых коммуникаций и других технологий на квантовых принципах. Участники соглашения — вузы, научно-исследовательские центры, инновационные компании и некоммерческие ассоциации, заинтересованные в совместном развитии квантовых технологий. Сформированный консорциум работает над формированием российской инфраструктуры квантовых коммуникаций и вычислений, разрабатывает стандарты и протоколы для работы устройств на квантовых принципах, а также исследует способы интеграции квантовой информатики в уже существующую коммуникационную сеть. Помимо этого, рабочая группа разработает консолидированную дорожную карту по развитию российских квантовых технологий.
Развитие квантовой инфраструктуры будет активно продвигаться в рамках Национальной технологической инициативы. В Москве, Санкт-Петербурге, Казани планируется запустить пилотные проекты по развитию квантовой инфраструктуры.
Исследователи из ИТМО создали систему квантовой связи для защищённой передачи данных на основе принципиально нового подхода. Система позволит передавать данные на расстояния более 250 километров, что не уступает самым современным зарубежным устройствам.
В Санкт-Петербургском государственном университете на математико-механическом факультете под руководством д. т.н., профессора Граничина О. Н. и д. т.н., профессора Терехова А. Н. ведутся работы по созданию гибридных сверхбыстрых компьютеров и системного программирования, а также проводятся исследования в области стохастического программирования и мультиагентных технологий.
В США в Лос-Аламосской национальной лаборатории создана линия связи общей длиной 48 км, в которой осуществляется распределение ключей со скоростью в несколько десятков Кбит/с. В университете Дж. Хопкинса реализована локальная вычислительная сеть с квантовым каналом связи длиной 1 км, в которой достигнута скорость передачи 5 кбит/с. В Великобритании, в Оксфордском университете, реализован целый ряд макетов квантово-криптографических систем с использованием различных методов модуляции и детектирования оптических сигналов. В лаборатории фирмы British Telecom получена наибольшая длина квантово-криптографической системы — 30 км при скорости передачи порядка 10 кбит/с. В эксперименте швейцарских исследователей каналом связи являлся подводный кабель длиной 23 км, используемый для передачи данных между Женевой и ее пригородом Ньоном.
К известным квантовым алгоритмам относятся: факторизация — ускорение сверхполиномиальное; нахождение дискретного логарифма двоичного числа — ускорение сверхполиномиальное; проверка произведения матриц — ускорение полиномиальное; решение задачи о сумме подмножеств — ускорение полиномиальное; решение линейных систем дифференциальных уравнений — ускорение сверхполиномиальное; структурированный поиск — ускорение константное; связанность вершин графа — ускорение полиномиальное; вычисление электрического сопротивления сложной цепи — ускорение экспоненциальное; путь в графе — ускорение сверхполиномиальное; вычисление ранга матрицы — ускорение полиномиальное; поиск подмножеств — ускорение полиномиальное; поток по сети — ускорение полиномиальное; квантовое преобразование Фурье — ускорение экспоненциальное. [4]
Краткие теоретические сведения: аналогично биту, кубит имеет два состояния 
. Кубит может находиться также и в квантовой суперпозиции этих двух состояний:
, где 
и 
— комплексные числа, удовлетворяющие так называемому условию нормировки
= 1. Вероятность обнаружить кубит в состоянии |
равна 
, а вероятность обнаружить его в состоянии |
равна 
. Пространство состояний квантовой системы — это векторное пространство. Такие векторные пространства относятся к классу гильбертовых пространств. [1, 2]
Для описания состояния кубита используются скобки 
в соответствии с так называемой нотацией Дирака. Эта система обозначений векторных величин также называется “bracket” (скобка) на два слога: bra («бра») вектор — строки и ket («кет») вектор –столбцы. Запись кет — вектора выглядит как 
, а бра — вектор записывается как 
В обозначении скалярного произведения два вектора оказываются заключенными в своеобразные скобки, например, 
. В матричной форме бра-векторы принято обозначать следующим образом: 
(1 0), 
(0 1). [1, 2]
В матричной форме кет-векторы принято обозначать следующим образом: |
, |
.
Одним из преимуществ записи векторов в дираковской системе является ее компактность, n — кубитовое базисное состояние описывается 
— мерным вектором. В рамках дираковской системы обозначений этот вектор будет представлен цепочкой длиной n, а вектор — столбец будет составлен из компонентов. Записать состояние 12 кубитов с помощью вектор столбца представляется достаточно трудоемким, так как число элементов в нем составит 
. Использование дираковской системы обозначений имеет и другие преимущества, которые становятся очевидными при работе с такими понятиями, как операторы и разного рода векторные произведения.
Ещё одним представлением состояния кубита является его наглядная геометрическая интерпретация в виде точки на единичной сфере, — сфере Блоха (рисунок 4). [2]
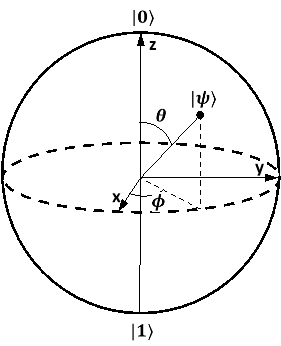
Рис. 4. Сфера Блоха
Северный и южный полюса сферы обычно выбираются под базисные состояния |
и |. Координатами точки служат два параметра 
и 
, которыми можно описать состояние кубита используя следующую формулу:
Квантовый компьютер является многокубитовым вычислительным устройством. Система из нескольких кубитов образует квантовый регистр. В классическом компьютере в каждый момент времени регистр представляет собой конкретную последовательность из 0 и 1 (рисунок 5). В квантовом компьютере регистр до измерения состояния не является точно определенным и описывается линейной композицией с комплексными числами n-битовых состояний вида:
.
Вероятность обнаружения квантового компьютера в состоянии 
равна 
, вероятность нахождения в состоянии 
равна 
, и т. д.
Рис. 5. Классический и квантовый регистры. Стрелкой показан вектор состояния кубита
К примеру, вектор состояния регистра из двух кубитов вычисляется с помощью произведения Кронекера (тензорного произведения) двух вектор-столбцов, описывающих состояния перемножаемых кубитов:
.
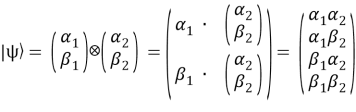тензорное произведение.
|
,
|
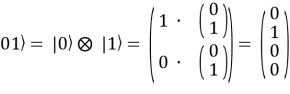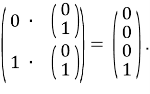
Любая логическая операция с кубитами называется квантовым вентилем, или гейтом. По числу кубитов преобразователи делятся на однокубитные и многокубитные. Преобразователь переводит одно состояние кубита (а в многокубитном случае — квантового регистра) в другое. Квантовым преобразованием называют унитарное преобразование вектора состояния квантовой системы. С квантовыми системами можно производить только линейные унитарные преобразования, при этом любое линейное унитарное преобразование допустимо. [5]
Скорее всего, все разработанные и реализованные к моменту создания квантового компьютера алгоритмы будут упакованы в некий «Фонд алгоритмов и программ», библиотеку квантовых алгоритмов, которая будет связана с устройством, выполняющим квантовые вычисления. Вполне вероятно, что это будет некий «квантовый сопроцессор», которым управляет обычный процессор при помощи каких-либо хитроумных устройств, которые позволяют выполнять две основные задачи: подготовка необходимых унитарных преобразований для выбранного квантового алгоритма и инициализация входных кубитов. На выходе этого «квантового сопроцессора» будут производиться измерения, а их результат сообщаться основному процессору, производящему вычисления. Таким образом, программировать само квантовое вычислительное устройство никто не будет; его будет «программировать» классический компьютер — настраивать гейты, связывать их друг с другом, инициализировать кубиты и запускать квантовые вычисления. [3]
Квантовая схема алгоритма Гровера представлена на рис. 6.
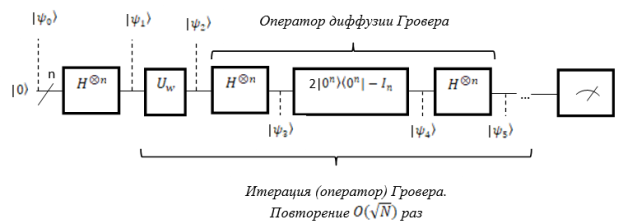
Рис. 6. Квантовая схема алгоритма Гровера
Рассмотрим неупорядоченную базу данных схемотехнических решений, содержащую 25000 файлов. Необходимо, быстро найти ровно один файл. Для того чтобы решить эту задачу на обычном компьютере, в худшем случае, придётся перебрать все 25000 файлов, а в среднем 12500. На квантовом компьютере необходимо и достаточно произвести 158 итераций, чтобы найти данный файл. В общем случае алгоритм Гровера позволяет выполнить поиск требуемой файла за 
шагов. [6]
Описание модели: программа для моделирования представляет собой функцию Grover(), принимающая в качестве параметров количество кубитов (параметр qbitsCountParam), порядковый номер искомого базисного состояния (параметр stateNumParam) и количество дополнительных итераций (параметр iterationsCountParam). Ниже пошагово рассмотрено подробное описание кода этой функции.
- Инициализация квантового регистра.
Состояние квантового регистра из n кубитов представляет собой произведение Кронекера (тензорное) вектор-столбцов состояний соответствующих кубитов, как показано в выражении:
,
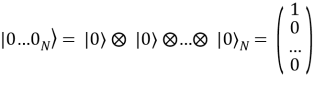где знак 
означает тензорное умножение, N — количество базисных состояний.
Расчета начального состояния регистра реализован в следующем коде с использованием встроенной функции произведения Кронекера kron():
Переменная qbit содержит вектор-солбец 
, являющийся выражением состояния 
. Результат вычисления состояния регистра для 2-х кубитов присвоен переменной registerState строкой ниже, а цикл for…endпредназачен для вычисления состояния регистра из 3 и более кубитов. Количество кубитов определяется по значению переменной qbitsCountParam, задаваемой пользователем при вызове пользовательской функции Grover(). Результат работы этого блока кода присваивается переменной registerState.
- Вычисление многокубитного гейта Адамара.
Матрица многокубитового гейта Адамара вычислена с помощью встроенной функции hadamard(). Эта функция в качестве параметра принимает размерность квадратной матрицы Адамара. Размерность равна количеству базисных состояний рассматриваемого регистра. Количество состояний N вычислено по формуле:
N = ,
где N — количество базисных состояний, а n — количество кубитов.
Так как функция hadamard() возвращает матрицу состоящую только из 1 и -1, то для получения матрицы многокубитового гейта Адамара необходимо полученную из этой функции матрицу умножить на коэффициент 
, где N — количество базисных состояний регистра. Блок этого кода выглядит как на листинге ниже.
Результат расчета матрицы многокубитного гейта Адамара присвоен переменной hadamardGate, а рассчитанное количество состояний регистра — переменной statesCount.
- Вычисление матрицы оракула.
Результатом расчета является переменная oracle, содержащая квадратную матрицу N x N с единицами по всем столбцам главной диагонали за исключением столбца, представляющего собой искомое состояние; в нем установлена -1. Расчет такой матрицы в соответствии с формулами расчета выглядит следующим образом:
В результате работы этого блока кода значение переменной oracle будет иметь вид, как на примере для 2-х кубитов и искомого 3-его состояния (
):
- Расчет матрицы условного фазового сдвига.
Каждое базисное состояние, за исключением 
в регистре приобретает фазовый сдвиг -1 в соответствии с выражением ниже:
В переменной faseShift сохранен результат расчета матрицы условного фазового сдвига в соответствии с формулой расчета.
- Вычисление количества итераций.
Количество итераций Гровера вычисляется по формуле:
где N — количество базисных состояний регистра.
Листинг кода, в котором реализован этот подсчет:
Использование встроенной функции fix() объясняется необходимостью взять от результата вычисления только целую часть.
- Применение преобразования Адамара.
Приготовление равновероятной (с равными амплитудами) суперпозиции состояний кубитов с помощью рассчитанной в шаге 2 многокубитовой матрицы Адамара:
.
В коде пользовательской функции Grover это преобразование применяется к переменной с инициализированным регистром registerState:
- Итерации Гровера.
Итерация Гровера (оператор Гровера) состоит из последовательно применяемых оракула, преобразования Адамара, условного сдвига фазы и ещё одного преобразования Адамара. Его состав наглядно показан на схеме 1.
Блок кода, реализующий логику работы этого оператора представлен листинге 7.
Используемый цикл for…end предназначен для выполнения оператора Гровера количество раз, равное значению переменной iterationsCount. Значение этой переменной было вычислено на шаге 5.
Здесь можно видеть как последовательно применяются преобразования к квантовому регистру, состояния которого представлены переменными с префиксом ‘state..’ в наименовании.
- Вывод результата.
Результатом работы функции является вектор-столбец, состоящий из амплитуд вероятности и график распределения вероятности по базисным состояниям. Возврат значения функцией Grover осуществляется строкой кода, представленной ниже.
Встроенная функция abs() нужна для получения абсолютных значений.
Демонстрация работы программы: полный код функции и примеры его выполнения с графиками приведены ниже.
function grover = Grover(qbitsCountParam, stateNumParam, iterationsCountParam)
if ~(qbitsCountParam > 0 && stateNumParam > 0 && stateNumParam <= 2^qbitsCountParam)
error('Ошибка параметра. ' +...
'Количество кубитов должно быть больше 0, ' +...
'а номер указанного во втором параметре номер состояния должен быть от 1 до 2^n, где n - количество кубитов.');
end
% Инициализация
% Определение кубита в состоянии 0.
qbit = [1; 0];
% Расчет количества базисных состояний
statesCount = 2^qbitsCountParam;
% Расчет состояния двухкубитового регистра.
state0 = kron(qbit, qbit);
% Расчет состояния регистра при 3 и более кубитов
for i = 3 : qbitsCountParam
state0 = kron(state0, qbit);
end
% Расчет гейта Адамара
hadamardGate = 1/sqrt(statesCount) * hadamard(statesCount);
% Расчет матрицы условного фазового сдвига
faseShiftDensityMatrix = state0 * transpose(state0);
I = eye(statesCount);
faseShift = 2 * faseShiftDensityMatrix - I;
% Расчет матрицы оракула
oracle = zeros(statesCount);
oracle(stateNumParam, stateNumParam) = 1;
oracle = I - 2 * oracle;
% Расчет количества итераций
iterationsCount = fix( (pi/4) * sqrt( statesCount)) + iterationsCountParam;
% 1-ое состояние. Применение гейта Адамара к начальному состоянию регистра
state1 = hadamardGate * state0;
% Начало оператора Гровера.
for i = 1 : iterationsCount
% 2-ое состояние. Применение оракула.
state2 = oracle * state1;
% 3-е состояние. Применение гейта Адамара к результату оракула
state3 = hadamardGate * state2;
% 4-ое состояние. Применение условного сдвига фазы
state4 = faseShift * state3;
% 5-ое состояние. Применение гейта Адамара к результату выполнения
% условного фазового сдвига. Заключительный шаг оператора Гровера.
state5 = hadamardGate * state4;
% запоминаем конечное состояние текущей итерации, перезаписывая им
% начальное состояние для следующей итерации.
state1 = state5;
end
plotGraph();
grover = abs(state5);
function plotGraph()
xVals = 0:statesCount - 1;
xVals = categorical( ...
cellstr( dec2bin( xVals, qbitsCountParam)));
bar(xVals, abs(state5));
ylim([0 1]);
end
end
Симуляция алгоритма Гровера для 2-х кубитов, искомого 3-его состояния и без дополнительных итераций:
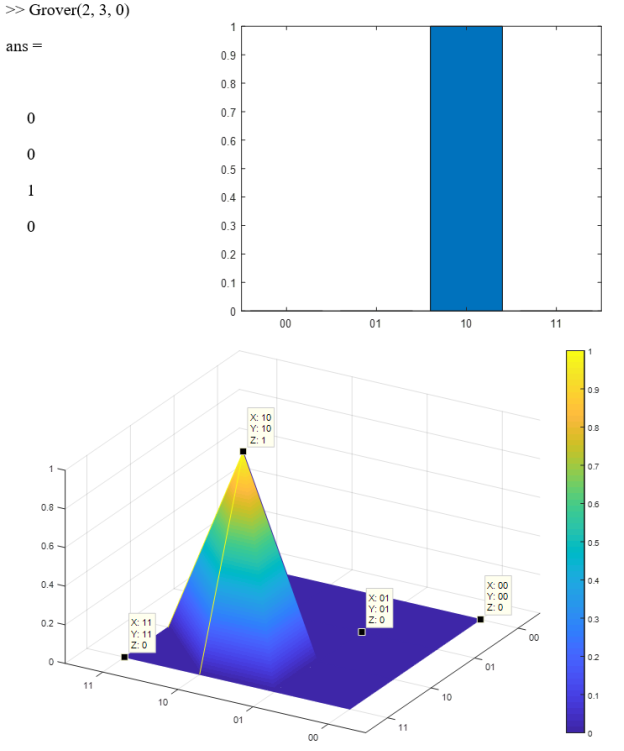
Симуляция алгоритма Гровера для 3-х кубитов без дополнительных итераций:
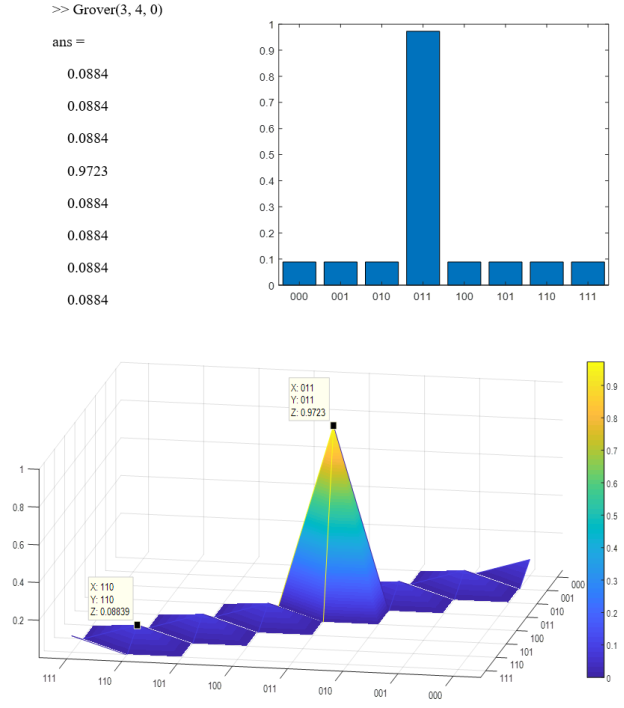
Контрольный пример для 4-х кубитов, искомого 5-ого состояния и без дополнительных итераций:
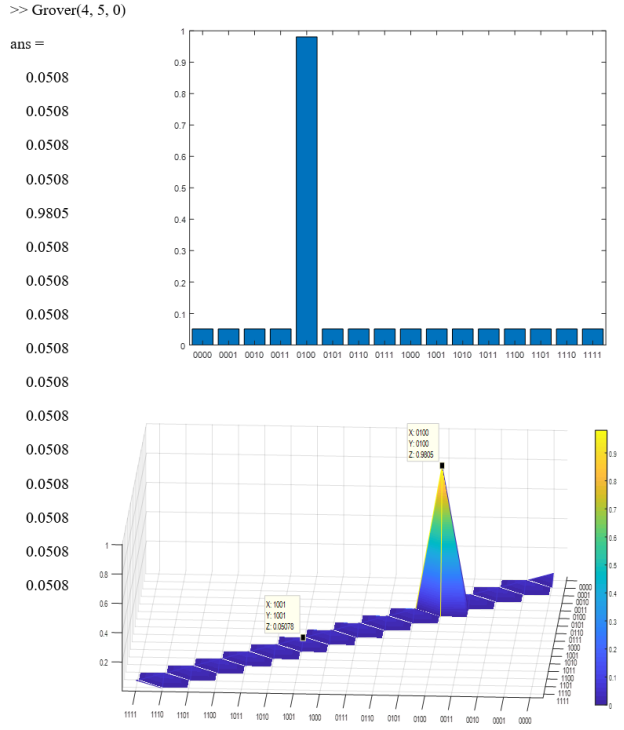
Поскольку алгоритм Гровера является вероятностным, он выдаст правильный ответ только с какой-то очень высокой вероятностью. Таким образом, например, в случае с двумя кубитами, выполнив одну итерацию мы нашли функцию, которая принимает значение 1 только на одном из 4-х вариантов входных значений. Следовательно, процедура поиска заметно ускорилась теоретически на 
по сравнению с расчетами на классическом компьютере. [2]
Если попробовать увеличить количество итераций, свыше расчетного количества, то результаты исказятся. Амплитуда вероятности искомого базисного состояния в таком случае станет уменьшаться, а остальные амплитуды — увеличиваться, приводя к ошибочным результатам. [4]
Так, к примеру, если выполнить функцию Grover для поиска 4-ого состояния в 3-х кубитном регистре с дополнительной 1 итерацией, то результаты будут следующие:
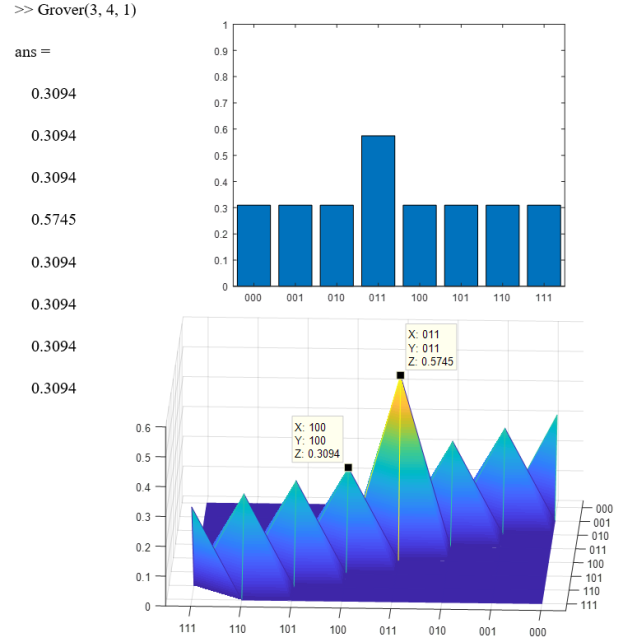
Литература:
1. Masahito Hayashi, Satoshi Ishizaka, Akinori Kawachi, Gen Kimura, Tomohiro Ogawa. Introduction to Quantum Information Science. — 1. — Berlin: Springer-Verlag Berlin Heidelberg, 2015 г. — 332 с.
2. Нильсен М., Чанг И. Квантовые вычисления и квантовая информация. Пер. с англ. — М.: Мир, 2006 г. — 824 с.
3. Валиев К. А., Кокин А. А. Квантовые компьютеры: надежды и реальность. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001 г. — 352 с.
4. Душкин Р. В. Квантовые вычисления и функциональное программирование. — 2014 г. — 318 с.
- Чивилихин С. А. Учебное пособие “Квантовая информатика”. — 2009г.
- Актимиров А. В. Реализация квантовых вычислений в программе Excel / Актимиров А. В.// Молодой ученый. — 2015 № 22 — с. 16–21
