Рассматривается численная модель открытой системы массового обслуживания с ограничениями. Изложен процесс получения некоторых неизвестных аналитических формул характеристик системы на основе вспомогательных функций программы, реализующей данную модель.
Ключевые слова: система массового обслуживания, характеристики системы, моделирование, аналитические формулы
Процесс установления неизвестных аналитических формул систем массового обслуживания (СМО) открытого типа [1] при помощи реализованной численной модели [3] включает следующие шаги:
1. Выявление принципа вычисления динамической величины указанной характеристики на этапе создания и отладки алгоритма [2], моделирующего исследуемую СМО.
2. Определение оптимальных сочетаний [3] входных параметров СМО, при которых минимальна общая погрешность динамических значений, либо погрешность значений, объединенных общим признаком, зависимость от которых искомой величины очевидна. Найденные наборы параметров позволят исключить влияние генераторов случайных чисел (ГСЧ) системы [4] на результаты.
3. Анализ установленных ранее зависимостей, попытка определения формулы методом подбора при помощи реализованного в программе инструмента «Испытание формул» [3], который позволяет вычислять в реальном времени значения формулы для сохраненных наборов входных параметров и сравнивать с динамическими значениями величин, полученных и отобранных по определенным критериям из испытаний [3].
4. Перебор при помощи «Испытания формул» [3] сомножителей и слагаемых, образующих формулу, либо некоторую её часть, и определение соответствующего набора, при котором погрешность между динамическим и статическим значением будет минимальна для всех выбранных сочетаний входных параметров СМО. При равной погрешности двух формул алгоритм выбирает ту, которая записана меньшим количеством символов, по окончанию перебора программа предоставляет информацию о формулах, выбранных более 1 раза, а также формулах с наименьшей средней и минимальной погрешностями.
Стоит отметить, что описанные шаги не определяют строго последовательность действий при установлении неизвестной аналитической формулы. Та или иная формула может быть обнаружена на каждом из этих шагов по отдельности, однако, указанная последовательность действий позволяет структурировать полученные результаты. Шаг № 4, не смотря на трудоемкость и временные затраты описанной процедуры, как правило оказывается лишь вспомогательным инструментом, т. к. анализ результатов и принятие решения остается за исследователем. Тем не менее, при определенной сноровке при помощи этого инструмента появляется возможность подобрать формулу, либо её часть, имеющую наименьшие погрешности, а, следовательно, аппроксимирующую свойства искомой характеристики. Рассмотрим многоканальную СМО с неограниченной очередью.
1. Среднее число требований обслуженных подряд за период частичной и полной занятости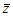 
. В первый раз формула была найдена в результате эксперимента (по аналогии с формулой для одноканальной модели), а лишь затем выведена аналитически. Смысл динамической величины: число требований, поступивших на обслуживание подряд, разделенные требованиями, заставшими обслуживающий прибор свободным. Очевидно, формула содержит вероятность того, что поступившее требование застанет обслуживающий прибор свободным 
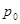. Разделив число всех требований, поступивших в систему на число требований, заставших обслуживающий прибор свободным, мы получим искомую величину, однако, заменим первую величину на вероятность пребывания в системе любого числа требований, а вторую на вероятность отсутствия требований в системе.
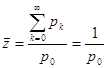(1)
В данной формуле в число обслуженных подряд требований входит то, с которого начинается подсчет (заставшее обслуживающий прибор свободным). Исключив его из формулы (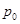
в числителе), получим число требований, поступивших в систему за период частичной и полной занятости.
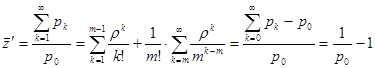(2)
Для проверки найденной формулы, как и последующих в данной модели, используется следующий набор входных параметров: интенсивность потока требований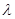 
и потока обслуживания 
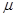в диапазоне 
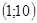с шагом 0.5, число каналов в диапазоне 
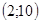с шагом 1, также ограничено отношение приведенной интенсивности потока требований к числу обслуживающих каналов 
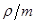интервалом 
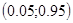. Максимальная, средняя и минимальная относительная погрешность 
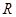данной величины: 
, 
, 
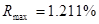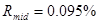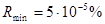. Погрешность данной величины растёт при 
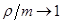. График зависимости значений формулы (1) от приведенной интенсивности потока требований 
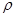при различных значениях числа обслуживающих каналов 
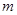показан на рис. 1. Для наглядности большая часть графиков величин будет представлена в логарифмическом виде.
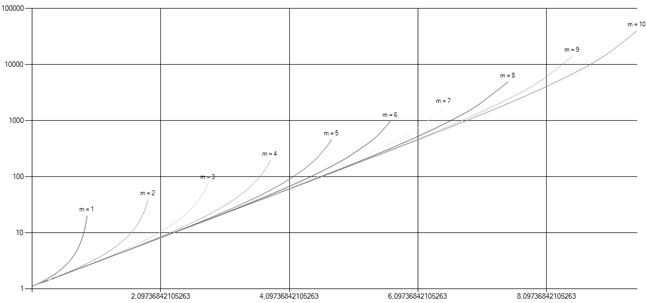
Рис. 1. Среднее число требований, обслуженных подряд при частичной и полной занятости для СМО с неограниченной очередью
2. Среднее время непрерывной работы прибора при частичной и полной занятости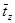 
. Смысл динамической величины: среднее время существования обслуживающего прибора, в течение которого он обслуживал поступающие подряд требования. Данная формула была получена из (2) по аналогии с обобщенными формулами Литтла [1, с. 190].
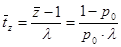(3)
Формула выражает математическое ожидание суммы промежутков времени между поступающими подряд требованиями. Максимальная, средняя и минимальная относительная погрешность 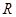данной величины: 
, 
, 
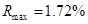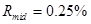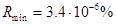. Погрешность данной величины растёт при 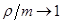. График зависимости значений формулы (3) от приведенной интенсивности потока требований 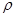при различных значениях числа обслуживающих каналов 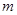показан на рис. 2. Интенсивность потока требований для данного графика фиксирована.
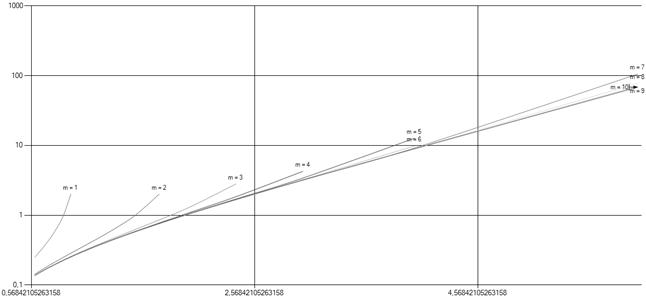
Рис. 2. Среднее время непрерывной работы прибора при частичной и полной занятости для СМО с неограниченной очередью
3. Среднее число требований обслуженных подряд за период полной занятости прибора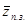 
. Данная формула была получена также в результате экспериментов, а лишь затем выведена аналитически. Значения данной характеристики для многоканальной СМО с неограниченной очередью совпадают со средней длиной реальной очереди, однако, как будет показано далее, сама величина отличается. Смысл динамической величины: число требований, поступивших на обслуживание подряд при полной занятости обслуживающего прибора, либо непрерывно занимающие последний свободный канал, разделенные требованиями, заставшими на обслуживающем приборе 
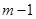занятых каналов (при этом обслуживание не было непрерывным).
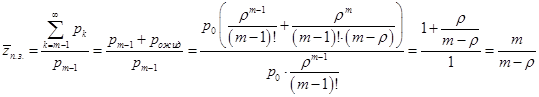(4)
Формула выражает математическое ожидание числа требований, заставших обслуживающий прибор занятым, которые приходятся на 1 требование, заставшее на обслуживающем приборе 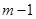занятых каналов. В данной формуле в число обслуженных подряд требований входит то, с которого начинается подсчет (заставшее 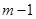занятых каналов). Исключив его из формулы (
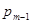в числителе), получим число требований, поступивших на обслуживание за период полной занятости.
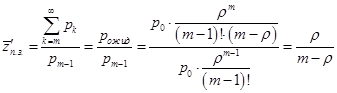(5)
Максимальная, средняя и минимальная относительная погрешность 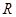данной величины: 
, 
, 
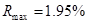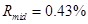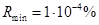. Погрешность данной величины растёт при 
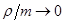. График зависимости значений формулы (4) от приведенной интенсивности потока требований 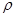при различных значениях числа обслуживающих каналов 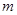показан на рис. 3.
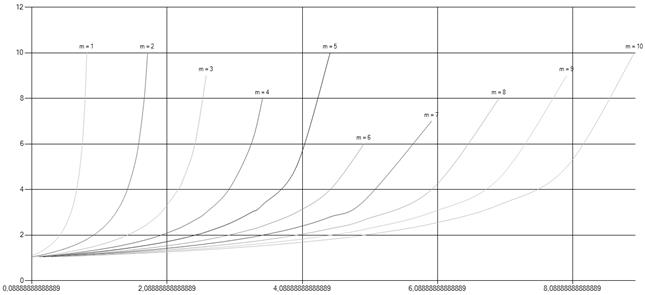
Рис. 3. Среднее число требований, обслуженных подряд при полной занятости, для СМО с неограниченной очередью
4. Дисперсия числа требований, обслуженных подряд при полной занятости прибора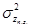 
. Данная формула была получена в результате перебора сочетаний-множителей при помощи инструмента «Испытание формул».
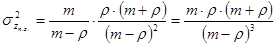(6)
Максимальная, средняя и минимальная относительная погрешность 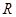данной величины: 
, 
, 
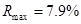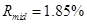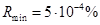. Погрешность данной величины растёт пр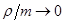и и 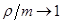. График зависимости значений формулы (6) от приведенной интенсивности потока требований 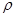при различных значениях числа обслуживающих каналов 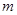показан на рис. 4.
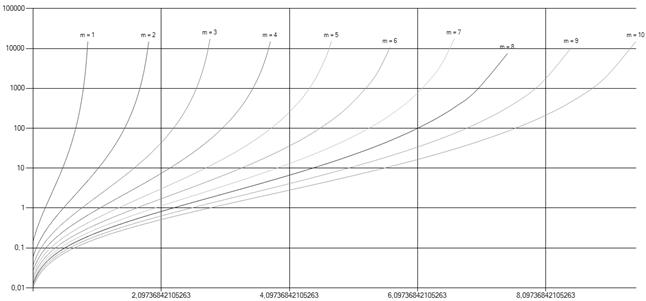
Рис. 4. Дисперсия числа требований, обслуженных подряд при полной занятости, для СМО с неограниченной очередью
5. Среднее время непрерывной работы прибора при полной занятости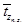 
. Смысл динамической величины: среднее время существования обслуживающего прибора, в течение которого он обслуживал поступающие подряд требования, при этом все 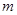каналов были заняты. Данная формула была получена из (5) по аналогии с обобщенными формулами Литтла [1, с. 190].
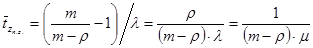(7)
Формула выражает математическое ожидание суммы промежутков времени между поступающими подряд требованиями при 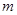занятых каналах. Максимальная, средняя и минимальная относительная погрешность 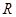данной величины: 
, , 
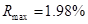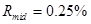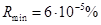. Погрешность данной величины растёт пр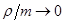и и 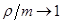. График зависимости значений формулы (7) от приведенной интенсивности потока требований 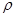при различных значениях числа обслуживающих каналов 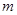показан на рис. 1.5. Интенсивность потока требований для данного графика фиксирована.
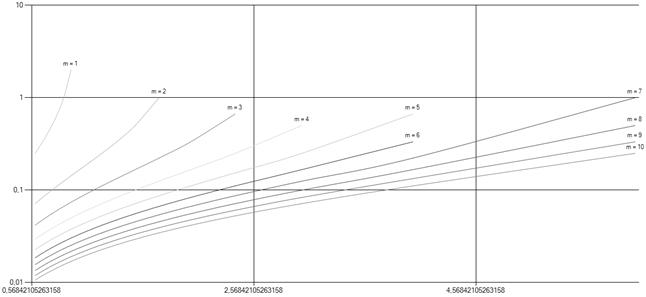
Рис. 5. Среднее время непрерывной работы прибора при полной занятости для СМО с неограниченной очередью
6. Дисперсия времени непрерывной работы прибора при полной занятости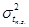 
. Данная формула была получена в результате перебора сочетаний-множителей при помощи инструмента «Испытание формул», основываясь на формуле (6) и обобщенных формулах Литтла [1, с. 190].
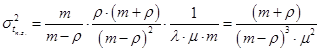(8)
Максимальная, средняя и минимальная относительная погрешность 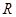данной величины: 
, 
, 
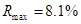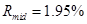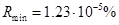. Погрешность данной величины растёт пр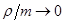и и 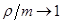. График зависимости значений формулы (8) от приведенной интенсивности потока требований 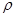при различных значениях числа обслуживающих каналов 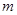показан на рис. 6. Интенсивность потока требований для данного графика фиксирована.
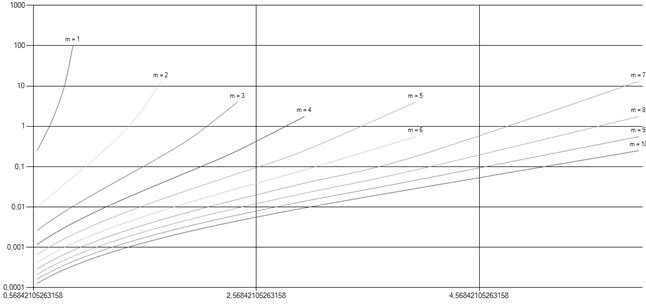
Рис. 6. Дисперсия времени непрерывной работы прибора при полной занятости для СМО с неограниченной очередью
7. Среднее число требований обслуженных подряд за период не полной занятости прибора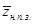 
. Формула была получена благодаря объединению аналитической интерпретации величины по аналоги с формулами (1) и (4) и поиску недостающего коэффициента при помощи инструмента «Испытание формул». Смысл динамической величины: число требований, поступивших на обслуживание подряд, занявшие от 
до 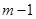свободных каналов, и разделенные требованиями, заставшими обслуживающий прибор свободным или заставшими в системе 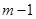занятых каналов. Очевидно, формула содержит вероятность того, что поступившее требование застанет обслуживающий прибор свободным 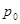, вероятность застать 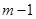требование в системе, а также некоторые другие величины.
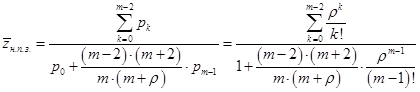(9)
В числителе через вероятность пребывания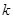 
требований в системе выражены требования, обслуженные подряд при не полной занятости, в знаменателе же находится количество случаев непрерывного обслуживания, которое содержит требования, заставшие обслуживающий прибор свободным, а также заставшие 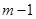требование в системе, при условии, что предыдущее требование застало 
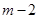занятых канала. Это связано с тем, что подсчет величины не включает случаи, при которых среднее число требований, обслуженных подряд при не полной занятости, равно нулю, т. е. при переходе в состояние системы 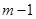из состояния 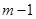или 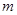. Коэффициент 
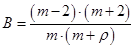равен вероятности перехода в состояние 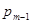из состояния 
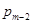, а не 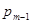или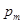 
. Максимальная, средняя и минимальная относительная погрешность 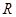данной величины: 
, 
, 
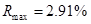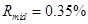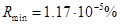. Погрешность данной величины растёт при 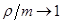, а также при числе каналов 
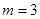. График зависимости значений формулы (9) от приведенной интенсивности потока требований 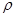при различных значениях числа обслуживающих каналов 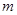показан на рис. 7.
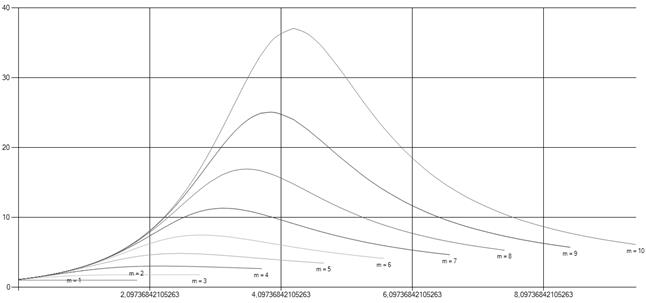
Рис. 7. Среднее число требований, обслуженных подряд при не полной занятости, для СМО с неограниченной очередью
При помощи созданного программного обеспечения [3], моделирующего многоканальные системы массового обслуживания открытого типа с ограничениями [1], а также обладающего широким функционалом и удобным интерфейсом, получены аналитические формулы следующих величин:
1. Среднее количество требований, обслуженных подряд при частичной и полной занятости, а также при полной и не полной занятости обслуживающего прибора.
2. Среднее время непрерывной работы обслуживающего прибора при частичной и полной занятости, а также при полной и не полной занятости.
Вспомогательные инструменты данного программного обеспечения, реализованные для исследования зависимостей характеристик, определения аналитических формул и удобного представления результатов, позволяют упростить процесс исследования, а также возложить часть действий (порой большую) на ЭВМ.
Литература:
1. А. П. Кирпичников, Методы прикладной теории массового обслуживания. Казань, Изд-во Казанского университета, 2011. 200 с.
2. Шемахин Е. Ю., Кирпичников А. П. Моделирование многоканальных открытых систем массового обслуживания с ограничениями в среде Visual Studio 2010, Вестник Казанского технологического университета. 2015. Т.18, № 3.
3. Шемахин Е. Ю., Моделирование СМО открытого типа. Проверка численной модели, «Вестник науки и образования». 2015. № 2(4).
4. Шемахин Е. Ю., Моделирование СМО открытого типа. ГСЧ, «European research». 2015. № 2(3).
5. Microsoft Developer Network. [Электронный ресурс]: Руководство по программированию на C#. URL: https://social.msdn.microsoft.com/Search/ru-RU (дата обращения: 28.10.2014).
