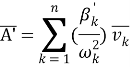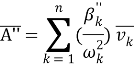В статье производится оценка сходимости результатов прямого динамического расчета на гармоническую нагрузку, выполненного аналитическим методом и методом конечных элементов с использованием программных комплексов.
Ключевые слова: метод конечных элементов, динамический расчет, гармонические колебания, расчетная схема, верификация.
Исходные данные для расчета: статически определимая система с 2-мя степенями свободы, l = 2 м, E = 3310000 т/м 2 , I = 312500 см 4 , m 1 = 3 т, m 2 = 1 т. Гармоническая нагрузка — P 0 = 10 т. Резонансная частота = ɷ 2. Коэффициент неупругого сопротивления у=0,1. Расчетная схема приведена на рисунке 1.
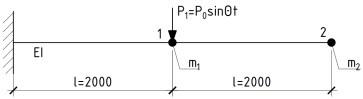
Рис. 1. Расчетная схема
Сравнение результатов аналитического расчета будет проводиться с расчетами методом конечных элементов, выполненными в программных комплексах «SCAD ++» версия 21.1.1 и версия 21.9.7.
Для построения расчетных схем использован тип конечного элемента 2 — стержень плоской рамы. Количество узлов в расчетной схеме 21, количество элементов — 20. Для решения задачи используется расчет на динамические воздействия. В качестве воздействия применены гармонические колебания. Количество форм учитываемых колебаний — 2.
Решим задачу аналитическим методом. По формуле Мора с использованием правила Верещагина определим элементы матрицы податливости от действия единичных сил инерции. Перемножая полученные эпюры моментов от единичных усилий получим элементы матрицы податливости А:
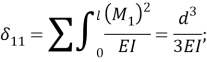
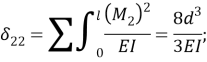
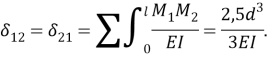
Упростив выражения приведем значения перемещений и масс к безразмерным величинам
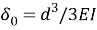
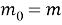
Вводим матрицу С=АМ, где А — матрица податливости, М — диагональная матрица масс и получаем выражение [2]:
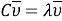
где υ и — собственные вектора и собственные числа матрицы С.
Составим характеристическое (частотное) уравнение:
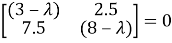
Развернув определитель и решив квадратное уравнение относительно находим корни характеристического уравнения (собственные числа матрицы С):
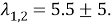
Получим частоты собственных колебаний [1]:


Далее вычисляем компоненты собственных векторов
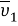
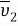
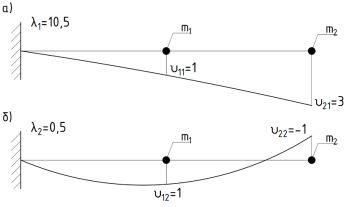
Рис. 2. Отображение форм собственных колебаний (а — 1 форма собственных колебаний, б — 2 форма собственных колебаний)
На рисунке 3 приведены отображения форм колебаний по 1 и 2 формам колебаний, полученные в программных комплексах.
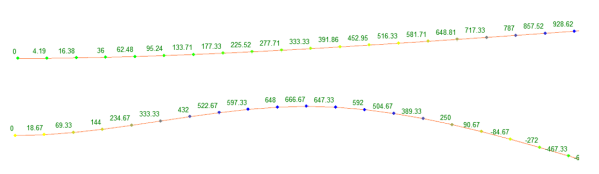
Рис. 3. Отображение форм колебаний, полученных в ПК «SCAD++»
В таблице 1 приведено сравнение результатов расчета собственных частот колебаний, полученных аналитическим расчетом и методом МКЭ.
Таблица 1
Сравнение результатов расчета собственных частот колебаний
|
Собственная частота |
Аналитический метод |
ПК «SCAD++» 21.1.1 |
ПК «SCAD++» 21.9.7 |
Погрешность |
|
1 форма колебаний |
60 рад/сек |
60.2 рад/сек |
60.2 рад/сек |
0.33 % |
|
2 форма колебаний |
275 рад/сек |
275.87 рад/сек |
275.87 рад/сек |
0.33 % |
Определим внутренние усилия с учетом сил сопротивления при установившихся вынужденных колебаниях системы с резонансной частотой θ= ɷ 2 . Сумма данных составляющих по первой и второй формам колебаний дает силы S' 1 , S' 2 и S 1 '', S 2 ''(рисунок 4, а) от которых на рисунке 4, б изображены эпюры изгибающих моментов М' и М» [2].
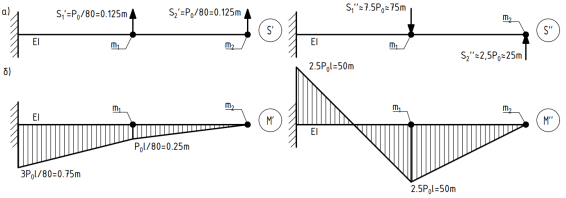
Рис. 4. Внутренние усилия системы (а — численные значения сил S' и S'', б — эпюры изгибающих моментов М' и М»)
Произведём сравнение внутренних усилий, полученных методом конечных элементов с усилиями полученными аналитическим методом. На рисунках 5, 6 приведены значения динамических сил S' и S'' и моментов М' и М'', полученных в ПК «SCAD++» версии 21.1.1, на рисунках 7 и 8 то же для ПК «SCAD++» версии 21.9.7.

Рис. 5. Значения динамических сил, полученных в ПК «SCAD++» версия 21.1.1 (а — S'; б — S'')
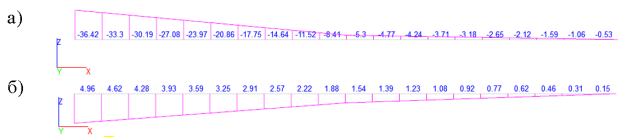
Рис. 6. Значения изгибающих моментов, полученных в ПК «SCAD++» версия 21.1.1; (а — М'; б — М''')

Рис. 7. Значения динамических сил, полученных в ПК «SCAD++» версия 21.9.7 (а — S'; б — S'')
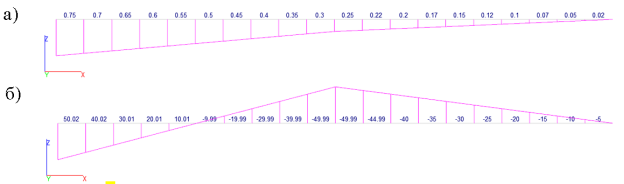
Рис. 8. Значения изгибающих моментов, полученных в ПК «SCAD++» версия 21.9.7; (а — М'; б — М''')
В таблице 2 приведено сравнение результатов расчета внутренних усилий, полученных аналитическим расчетом и методом конечных элементов.
Таблица 2
Сравнение результатов расчета внутренних усилий
|
Усилие |
Соста-ляющая |
№ точки |
Аналит. метод |
ПК «SCAD++» 21.1.1 |
Погр-ть |
ПК «SCAD++» 21.9.7 |
Погр-ть |
|
S |
S' |
1 |
0.125 т |
12.91 т |
10228 % |
0.13 т |
4 % |
|
2 |
0.125 т |
2.65 т |
2020 % |
0.12 т |
4 % | ||
|
S'' |
1 |
75 т |
0.94 т |
98.8 % |
75 т |
0 % | |
|
2 |
25 т |
0.77 т |
96.9 % |
25 т |
0 % | ||
|
M |
M' |
1 |
0.25 т |
5.13 т∙м |
1952 % |
0.25 т∙м |
0 % |
|
2 |
0.75 т |
36.42 т∙м |
4756 % |
0.75 т∙м |
0 % | ||
|
M'' |
1 |
50 т∙м |
1.54 т∙м |
69.2 % |
49.99 т∙м |
0.02 % | |
|
2 |
50 т∙м |
4.96 т∙м |
9.92 % |
50 т∙м |
0 % |
Полученные аналитическим методом значения и значения, полученные методом конечных элементов в ПК «SCAD++» версии 21.9.7 различаются менее чем на 1 %, при этом значения мнимой составляющей отображаются в противофазе относительно аналитического расчета. Полученные значения в ПК «SCAD++» версии 21.1.1 существенно отличаются от результатов, полученных аналитическим методом не только по величине полученных усилий, но и по характеру их распределения. Как видно из таблицы 2, доминирующее значение имеют составляющие отвечающие действительной составляющей внутренних усилий, в то время как аналитическим расчетом подтверждено подавляющее влияние сил, отвечающих мнимой составляющей.
Амплитудные значения перемещений узлов с учетом сил сопротивления при установившихся вынужденных колебаниях системы с резонансной частотой = ɷ 2 получим исходя из зависимостей [3]:
|
|
|
Сумма составляющих по первой и второй формам колебаний дает амплитуды А' 1 , А' 2 и А 1 '', А 2 ''(рисунок 9).

Рис. 9. Суммарные значения амплитуд А' и А''
Произведём сравнение амплитуд колебаний, полученных методом конечных элементов с амплитудами, полученными аналитическим методом. На рисунках 10 и 11 приведены значения амплитуд колебаний А' и А'', полученных в ПК «SCAD++» версий 21.1.1 и 21.9.7 соответственно.

Рис. 10. Значения амплитуд колебаний, полученных в ПК «SCAD++» версии 21.1.1; (а — амплитуд колебаний А'; б — амплитуд колебаний А'')
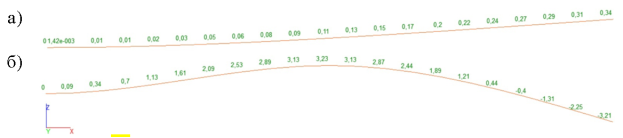
Рис. 11. Значения амплитуд колебаний, полученных в ПК «SCAD++» версии 21.9.7; (а — амплитуд колебаний А'; б — амплитуд колебаний А'')
В таблице 3 приведено сравнение результатов расчета амплитуд колебаний, полученных аналитическим методом и методом МКЭ.
Таблица 3
Сравнение результатов расчета амплитуд колебаний
|
Амплитуда колебаний |
№ точки |
Аналитический метод |
ПК «SCAD++» 21.1.1 |
Погрешность |
ПК «SCAD++» 21.9.7 |
Погрешность |
|
А' |
1 |
0.11 |
5.04 |
4481 % |
0.11 |
0 % |
|
2 |
0.34 |
13.78 |
3952 % |
0.34 |
0 % | |
|
А'' |
1 |
3.22 |
0.74 |
77 % |
3.23 |
0.31 % |
|
2 |
3.22 |
2.19 |
32 % |
3.21 |
0.31 % |
Полученные аналитическим методом значения и значения, полученные методом конечных элементов в ПК «SCAD++» версии 21.9.7 различаются менее чем на 1 %. Полученные значения методом конечных элементов в ПК «SCAD++» версии 21.1.1 значительно отличаются от результатов, полученных аналитическим методом. Анализируя данные, приведенные на рисунке 10(б), можно сделать вывод, что общий вид деформации стержня не совпадает с отображением формы колебаний на рисунке 3.
В настоящее время большинство программных комплексов позволяют выполнить прямой динамический расчет сложных конструктивных систем и облегчить работу инженеру — конструктору. Проведенное сравнение результатов аналитического расчета с результатами расчетов в программных комплексах подтверждают необходимость дополнительной проверки результатов задач, решаемых в программных комплексах. В связи с тем, что разработчики программных комплексов регулярно совершенствуют свои продукты на основе обратной связи от инженерного сообщества, достоверность результатов сильно зависит не только от наименования программного комплекса в котором производится прямой динамический расчет, но и от его версии. Необходимость самостоятельной проверки результатов может быть дополнительно обоснована тем, что в верификационных тестах, разработчики приводят необходимый, но все-таки не полный отчет по всем имеющимся в программных комплексах функциям.
Литература:
- Справочник по динамике сооружений. Под ред. Б. Г. Коренева, И. М. Рабиновича. М., Стройиздат, 1972 г. — 511 с.
- Строительная механика. Динамика и устойчивость сооружений. А. Ф. Смирнов, А. В. Александров, Б. Я. Лащеников, Н. Н. Шапошников, Стройиздат, 1984 г. — 414 стр.
- Инструкция по расчету несущих конструкций промышленных зданий и сооружений на динамические нагрузки ЦНИИСК им. В. А. Кучеренко, Стройиздат, 1970 г.