Методы инфлюентного анализа и принятие решений

В работе рассмотрен инфлюентный анализ числовых данных, имеющий математические выражения через методы: цепных подстановок, логарифмический метод или же через нахождение точки Эйлера-Лагранжа и др. Наиболее безошибочным отмечается интегральный метод, однако формулы данного метода весьма загромождены и сложны, поэтому на практике для упрощения вычислений используется логарифмирование. Инфлюентный анализ главным образом применяется при решении экономических задач, актуальных в настоящее время, а также может быть использован и для реализации усложненных технических систем управления.

Ключевые слова: метод, анализ, модель, принятие решений, инфлюентный анализ

The paper considers inflyuentny analysis of numerical data having the mathematical expression through methods: Chain substitutions, the logarithmic method, or by finding the Euler-Lagrange points, etc. The most unmistakable notes integral method, however, the formula of this method is very cluttered and complicated, so in practice, to simplify calculations using logarithms. In-flyuentny analysis is mainly applied in the solution of economic problems that are relevant at the moment, and it can also be used for the realization-complicates United technical control systems.

Keywords: method, analysis, model, decision-making, influential analysis

В настоящее время проблема принятия решений при недостаточных и неточных исходных данных образует крупное направление исследования методов решения многокритериальных задач. Выбор наилучшего варианта из предложенных усложняется несколькими факторами: во-первых, отсутствием формализированной связи между признаками и самими объектами, а во-вторых, необъективными исходными данными. Результатом этого становится недостаток объективной информации, который восполняется субъективными оценками экспертов на основании их эмпирических знаний, опыта и догадок. Оценка эксперта всегда связана с неопределенностью в силу своей субъективности, что в дальнейшем будет влиять на нечеткость выбранного решения.

Области применения математических и статистических методов для целей исследования систем организационного управления зависят от особенностей модели системы управления и вида исходных данных. Так, задачи синтеза удобнее и проще решать на детерᴍᴎʜироваʜных моделях, так как используемые при ϶ҭᴏᴍ методы требуют рассмотрения большого числа вариантов построений системы или перебора множества значений ее параметров для поиска лучшего соглаϲʜᴏ принятому критерию.

Целью работы является рассмотрение инфлюентного факторного анализа как одного из методов детерминированного анализа. На современном этапе развития науки проблема определения влияния факторов на конечный результат в абсолютном выражении недостаточно разработана, поэтому в работе сделан акцент на рассмотрение инфлюентного анализа. Рассматриваемые в работе методы решения задачи инфлюентного анализа формулируются алгоритмически и ориентированы на применение ЭВМ. Сравнение методов проводится применительно к случаю достаточно большого количества факторов. Основу теоретической базы, используемой при написании настоящей работы, стали труды Трухаева Р. И. и Мухина В. И.

Сущность иприменение инфлюентного анализа

Важнейшим аспектом статистического изучения показателей деятельности предприятия является факторный анализ, представляющий отдельную ветвь статистической методологии, исследующую методы оценки влияния отдельных факторов на изменение обобщающего показателя. Различают два типа факторного анализа. Факторный анализ Ч. Спирмена, Л. Тэрстоуна и других специалистов по математической статистике основан на ее методах и имеет основной задачей построение комплексов укрупненных факторов с целью экономного описания экспериментальных данных и оценку силы их влияния на зависимую величину. При экономическом, финансовом и инвестиционном анализе детерминированных зависимостей требуется иной тип факторного анализа, задачей которого является оценка величины приращения обобщающего показателя под влиянием изменения каждого фактора. Этот тип анализа назовем инфлюентным факторным анализом (ИФА).

В свою очередь темп роста или индекс изменения искомого значения У вычисляется по формуле, которую можно проиллюстрировать следующим образом:

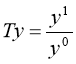
где у¹ представляет собой значение показателя в текущем периоде, у⁰ — значение того же показателя в базисном периоде. 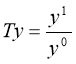==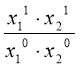Tx₁Tx₂

Даже, несмотря на то, что наука на данный момент находится на прогрессирующем этапе развития, проблема определения воздействия факторов на результат в конечном итоге в абсолютном выражении разработана в недостаточном объеме и требует постоянного внимания. Инфлюентный анализ служит обобщением методов, с помощью которых становится возможным определить оценки различного рода взаимосвязей между факторными изменениями и изменением значений показателя деятельности какой-либо системы известного как результирующий. Эти оценки (инфлюент) являются базой при организации процессов принятия решений в виде апостериорных действий, целью которых является усовершенствование и управление системой по уже озвученным выше базисным и текущим показателям.

Но нельзя не отметить, что даже при наличии достаточно обширной базы математических подходов и многочисленных взглядов на исследование перечисленных вопросов, при помощи факторного анализа нельзя в полной мере получить возможность найти оценки влияния факторов на присутствующие отклонения текущих значений от базисных. Данный факт неоспорим для случая многоцелевого показателя, и характерен для скалярного результирующего показателя. Тем не менее, никто не осмелится оспорить истину необходимости получения подобного рода оценок, потому как именно они служат первообразной для принятия самых объективных решений по совершенствованию и развитию организационных систем.

Детерминированный инфлюентный анализ ставит перед собой задачу определить искомый результирующий показатель У по заданной аналитической зависимости y=f(x1, x2,..., xn) от фиксированной совокупности факторов (x₁, x₂,..., x_n), далее нахождение инфлюент A(xi) как оценок изменения ∆xi=x1i – x0i фактора xi на величину ∆y=y1 – y0 изменения y в виде ∆y=A(x1) +...+ A(xn).

При оценке эффективности деятельности предполагаемой организации недостаточным будет лишь определение выручки или коэффициента рентабельность продаж, а также их изменения за отчетный период. Поэтому необходимо выявить, произошли ли какие-нибудь отклонения ввиду изменения факторов.

Проиллюстрировать функционирование подобного рода анализа можно с помощью примера деятельности n-го коммерческого банка. Прослеживается, что капитальное уравнение баланса банка, выражает некую зависимость отдачи собственного капитала (Y) от факторов, а именно: прибыльности (X₁), маржи прибыли (X₂), доходности активов (X₃) и мультипликатора капитала (X₄), и помимо этого представляет собой произведение 4-х факторов Y= X₁*X₂*X₃*X₄- иными словами, мультипликативную модель. Значения факторов предопределяют эффективность финансовой политики, проводимой банком, в частности, эффективность управления налогами, иными расходами, активами и имеющимися ресурсами банка, а их изменение обусловливает приращение капитала, образующего некую отдачу в отчетном периоде. Своей задачей инфлюентный факторный анализ считает оценивание влияния изменений факторов на прирост полученной отдачи капитала, а на ее основе уже оценить эффективность финансовой политики банка в прошлом, указать резервы роста и выработать меры на будущее.

Инфлюентный анализ относится к детерминированным методам анализа. Его суть заключается в определении влияния изменения параметров на ту величину, на которую отклоняется искомый показатель. Инфлюентный анализ применим при анализе процессов и систем управления. Возможность использования детерминированных методов анализа определяется возможностью дифференцирования (взятия полной или частной производной) как самой функции, так и числа ее переменных. В то же время говорить о внедрении инфлюентного анализа можно в том случае, если функция задана алгоритмически (то есть когда она задана определенной последовательностью каких-либо математических выражений, при этом учитывая достаточно большое число переменных). Из чего следует, что именно от дифференцирования функции и от количества составляющих ее переменных и зависит применение детерминированных методов.

Иными словами, суть инфлюентного анализа состоит в оценке влияния величины параметров Х, на величину изменений показателя Y.

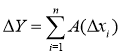
где - изменение значения показателя Y,

— изменение параметра х.

Составляющие разложения приращения называются инфлюентами, а инфлюентный анализ в свою очередь необходим для их определения, с последующим выявлением направленности и степени влияния изменения параметров

= ⁽¹⁾ —⁽⁰⁾ на изменение искомого показателя

= у⁽¹⁾ — у⁽⁰⁾.

Значения параметров и показателя{х_i⁽⁰⁾, у⁽⁰⁾, х_i⁽¹⁾, у⁽¹⁾} называются терминальными; за у⁽¹⁾ и х⁽¹⁾ принимаются фактические (реальные) значения, а за у⁽⁰⁾ и х_i⁽⁰⁾ — плановые (желаемые) значения.

При общей математической модели Y = f(х₁, х₂,..., х_n) наиболее простым и чаще используемым методом анализа является метод цепных подстановок, который, как видно из названия, заключается в подстановке в функцию Y в определенном порядке номинальных х_i⁽⁰⁾ и фактических х_i⁽¹⁾ параметров и вычислении результата по cледующим простым формулам:

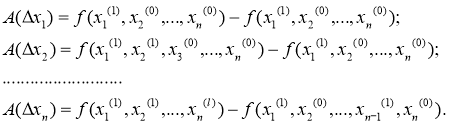
Но, к сожалению, не обойтись и без некоторых недостатков и неточностей: факторный анализ, используя реализацию метода цепных подстановок, не позволяет в полной мере оценить влияние отдельных факторов на отклонения фактических значений от плановых. Но, несмотря на данный факт, даже такие оценки имеют большое значение при принятии решений о методах совершенствования эффективности систем организационного управления, и эта задача будет также решаться с помощью использования все того же инфлюентного анализа.

Если попытаться провести краткий обзор методов, которые характерны для инфлюентного анализа, то можно выделить некоторые из них.

Логарифмический метод основан прежде всего на логарифмировании определенного вида зависимости (1), а далее представляет приращение показателя в виде: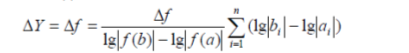

Одним из самых важных достоинств представленного метода является достаточная простота и отсутствие загроможденности его вычислительного алгоритма. Так как данный метод сводится к применению формулы к каждому фактору, причем коэффициент k требует вычисления лишь единожды, и немаловажным плюсом будет тот факт, что при этом расчеты могут быть выполнены при помощи простейших вычислительных средств.

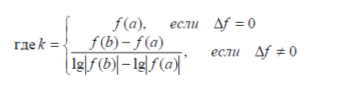
Далее имеет место упомянуть о следующем методе, таком как «Метод деления нераспределенных остатков поровну». В данном случае приращение мультипликативного показателя может быть представлено в следующем виде:

Выполнив действия над выражением, получим:

В соответствии с представленным методом, каждое из слагаемых, содержащихся в правой части выражения требует необходимого разделения равными долями между факторами, имеющими приращение, которое в свою очередь входит в это слагаемое в виде сомножителей. Это иллюстрируется тем, что первое слагаемое, к примеру, целиком относится к фактору первому и играет роль соответствующей составляющей инфлюенты A1, и наряду с этим слагаемое делится поровну между факторами 1 и 2 и т. д. Можно отметить результативность данного метода еще и тем уточнением, что для случая 2 и 3 факторов он может быть интерпретирован в геометрическом виде.

Следующим пунктом можно обозначить метод, известный как «Метод обратных колец». Его структура была предложена Н. Е. Гончаровым, и представляет собой, прежде всего, совершенствование метода цепных подстановок. При его использовании в качестве инфлюент обычно принято принимать величины, полученных в процессе осреднения значений, который вычисляются методом цепных подстановок при рассмотрении частности из n! Подстановок, которые возможны. Такие подстановки, принимаемые для расчета можно сформировать как раз путем кольцевой перестановки прямой и обратной последовательностей факторов. В этом случае число подстановок, которые мы можем рассматривать, оказывается тождественным 2n. Как утверждает автор данного метода, именно подобный выбор рассматриваемых подстановок получает те значения инфлюент, которые больше всего близки к средним значениям, получаемым в случае рассмотрения n! подстановок.

Если рассматривать инфлюентный анализ зависимостей произвольного ряда, то можно отметить, что этот так называемый раздел посвящен изучению методов, которые рассматриваются в случае, когда зависимость f(X) показателя от фактора произвольна. Но важно помнить, что при этом данная функция удовлетворяет тем условиям, которые необходимо учесть в обязательном порядке для применения какого-либо метода (будь то непрерывность, дифференцируемость или др.). Также указывается, что f(X) может быть задана как в аналитическом виде, так и в алгоритмическом.

Одними из наиболее адаптивных и простых методов, которые достаточно распространены и пригодны для инфлюентного анализа произвольных зависимостей является как раз метод цепных подстановок и метод точки Лагранжа. На последнем я остановлюсь наиболее подробно.

В математическом анализе формальная возможность получения выражений для инфлюент A(xi) содержится в интегральной формуле Эйлера-Лагранжа. Согласно этого подхода, изменение функции можно определить, если использовать в процессе вычислений криволинейный интеграл по отрезку прямой, соединяющей х и х_i.

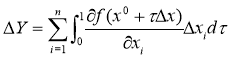
Из формулы получаем: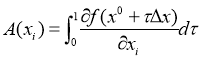, i=1,…,n

, i=1,…,n

Метод основывается на теоремах Лагранжа о среднем значении, называемых также теоремами о конечном приращении. Эти теоремы формулируются следующим образом:

Теорема 1. (для функции одной переменной). Если функция f(x) непрерывна на отрезке [a,b] и дифференцируема на отрезке (a,b), то в интервале (a,b) существует число X, соответствующее тождеству:

Теорема 2. (функция многих переменных) Если функция f (X₁, X₂,..., X_n) непрерывна при a_i ≤ X_i ≤ b_i и дифференцируема приa_iii(i=1,n), то существует набор таких чисел (X₁, X₂,..., X_n), что a_iii(i=1,n)и

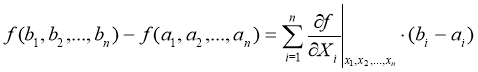
Таким образом, алгоритм численного определения инфлюент методом точки Ла-гранжа оказывается следующий:

1. Отыскивается (одним из методов поиска экстремума функции одной переменной, который в свою очередь не требует вычисления производных, как например, методом золотого сечения) значение 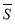, удовлетворяющее тождеству и позволяющее определить координаты точки Лагранжа X_i= a_i+ 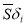(i=)

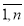2. Вычисляются (в численном или аналитическом видах) значения частных производных в найденной точке, которые, будучи умножены на величины приращений факторов δ_i, предопределяют значения инфлюент:

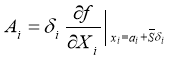
Отмечается, тем не менее, что рабочие формулы расчета инфлюент для мультипликативных моделей при помощи криволинейного интеграла (точка Эйлера-Лагранжа) в практике экономического анализа практически не используются из-за своей громоздкости и усложненности. В противовес ему, гораздо чаще используется логарифмический метод.

Рассмотрим факторную мультипликативную модель вида у=x₁x₂. Если прологарифмируем обе части тождества 3, то получим: =

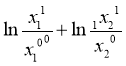
Получим окончательное выражение для разложения факторов, путем умножения обеих частей равенства на дробь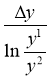

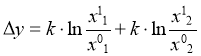
где

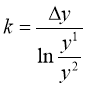
Если число параметров (факторов) в модели принять равным n, то инфлюенты вычисляются по достаточно простой формуле:

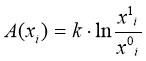
По значениям инфлюент первоначально упорядочивают параметры системы по силе их влияния на ее показатели, затем определяют, какого вида существует направленность этого влияния и в результате выделяют долю влияния каждого параметра относительно других.

Рассматриваемые в работе методы решения задачи инфлюентного анализа формулируются алгоритмически и ориентированы на применение ЭВМ. Сравнение методов проводится применительно к случаю, когда присутствует достаточно большое количество факторов.

Инфлюентный анализ ориентирован в основном на решение экономических задач, но равным образом может быть использован и для исследования сложных технических систем управления.

Анализ систем управления спомощью математических теорий

Принятие решений — само по себе это один из фундаментальных (базисных) этапов процесса управления, иными словами — этот тот выбор одного из вариантов или алгоритмов действий, которые должны быть направлены на достижение поставленных стратегических целей и задач.

Теория принятия решений как таковая является комплексной дисциплиной, которая напоминает о себе при случае, когда возникает необходимости сделать выбор альтернативы действий в условиях риска и/или при наличии неопределенности. Подобного вида необходимость может появляться в случаях, когда исходные данные представлены через определенные выражения, отображающие вероятностные характеристики (то есть опять же важно, что принятие решения имеет место также в условиях риска) либо же в ситуации, когда исходные данные заданы неопределенно, например, интервалами изменения или вообще только лишь одним названием.

Сама суть процесса принятия решения состоит в определении того, какой же управление наиболее допустимо из представленных альтернатив. В математической теории принятия решений есть и свои подводные камни: к примеру, субъективность как таковая отсутствует и остается лишь в выборе подходящего критерия вычислительной процедуры. Таким образом, лицу, опирающемуся в своих действиях на полученный результат, необходимо первоначально знать степень его оптимальности и затем — его надежность, т. е. величину риска.

Именно поэтому важным фактором является получение и разработка достаточной теоретической базы для обоснования какого-либо выбора метода анализа. Из вышесказанного можно сделать вывод о том, что алгоритм расчета напрямую зависит от того, какой вид имеют исходные данные (определенные и неопределенные), а также от критерия выбора решения и количества этапов принятия самих решений.

В качестве конечного результата принятия решений является именно то решение, которое представляет собой некое предписание к действию. Допустимым будет являться такое решение, которое удовлетворяет установленным ограничениям разного рода: ресурсным, правовым, этическим. Эффективность решения является обобщенной характеристикой решения. Она включает в себя эффект решения, который определяет степень достижения целей, отнесенный к затратам на их достижение. Итак, чем выше степень достижения целей и меньше затраты на их реализацию, тем решение будет эффективнее. Теория принятия решений — это совокупность понятий и систематических методов, позволяющих анализировать вопросы принятия решений в условиях неопределенности.

Для эффективного решения проблем и задач необходим комплексный подход с использованием основных положений анализа, статистики и синтеза систем управления. Выбор метода решения проблемы осуществляется в зависимости от того, какого вида необходимо решение, а также, если говорить об объекте управления, то — от степени соответствия потребностей и их удовлетворения, от вида переменной лимитирующей проблемы (задачи), квалификации специалистов. В случае если какой-нибудь метод на определенном этапе творческого процесса исчерпал себя, то следует рассмотреть другие методы, продумать какие их комбинации будут наиболее эффективными и приведут к продуктивному результату.

Выбор наиболее перспективного применения детерминированных методов зависит от возможности дифференцирования функции и числа переменных. При задании функции в алгоритмическом виде (то есть когда она определяется последовательностью математических выражений и при большом числе переменных) используется инфлюентный анализ.

В работе рассмотрен инфлюентный анализ числовых данных, имеющий математические выражения через методы: цепных подстановок, логарифмический метод или же через нахождение точки Эйлера-Лагранжа и др. Наиболее безошибочным отмечается интегральный метод, однако формулы данного метода весьма загромождены и сложны, поэтому на практике для упрощения вычислений используется логарифмирования. Инфлюентный анализ главным образом применяется при решении экономических задач, а также может быть использован и для реализации усложненных технических систем управления.

Использование детерминированных методов зависит от допустимости дифференцирования функции и числа переменных. Инфлюентный анализ необходим задании функции, а в алгоритмическом виде (то есть когда она определяется последовательностью математических выражений и при наличии большого числе переменных)

Таким образом, поставленная проблема была изучена, теоретические сведения обобщены и проиллюстрированы, а поставленные цели и задачи достигнуты.

Литература:

1. Трухаев Р. И. Инфлюэнтный анализ и принятие решений (детерминированный анализ). — М.: Наука, 1984.
2. Корн Г., Корн Т. Справочник по математике (для научных работников и инжене- ров) М., «Наука», 1977
3. Федоров В., Егоров Ю. К вопросу о разложении прироста на факторы. — Вестник статистики. — 1977. — № 5.
4. Гончаров Н. Е. Повышение качества факторного анализа на транспорте. — М.: Транспорт, 1982
5. Калиткин Н. Н. Численные методы. М., «Наука», 1978
6. Экономико-математические методы в анализе хозяйственной деятельности пред- приятий и объединений. Бушник-Сиверский А. В., Сайфулин Р. С., Рейльян Я. Р. и др. — М.: Финансы и статистика, 1982
7. Шеремет А. Д. Комплексный экономический анализ деятельности предприятий. — М.: Экономика, 1974.