Рассматриваются только конечные группы. Работа посвящена исследованию свойств τ-замкнутых Ω-композиционных и τ-замкнутых ω-центральных формаций конечных групп, где τ — подгрупповой функтор. Установлена взаимосвязь между минимальным τ-замкнутым ω-спутником ω-центральной формации и минимальным τ-замкнутым Ω-спутником Ω-композиционной формации. Для произвольной непустой неединичной τ-замкнутой формации ![]() построены τ-замкнутые Ω-композиционная и ω-центральная формации, содержащие
построены τ-замкнутые Ω-композиционная и ω-центральная формации, содержащие ![]() .
.
Ключевые слова: конечная группа, класс групп, формация групп, подгрупповой функтор, Ω-композиционная формация, ω-центральная формация.
Рассматриваются только конечные группы и классы конечных групп. Классом групп называется всякое множество групп, содержащее вместе с каждой своей группой и все группы, ей изоморфные. Одним из наиболее важных видов классов конечных групп являются формации, введенные в рассмотрение Гашюцем в 1963 году [1]. Формацией называется класс групп, замкнутый относительно гомоморфных образов и конечных подпрямых произведений. Основные положения теории формаций конечных групп представлены в монографиях Л. А. Шеметкова [2], А. Н. Скибы [3], Дерка и Хоукса [4] и др. В теории формаций конечных групп существенную роль играют функциональные методы, с помощью которых построены наиболее изученные в настоящее время локальные и композиционные формации (см. [2]), а также их обобщения — соответственно ω-локальные и Ω-композиционные формации. Дальнейшее развитие функциональные методы получили в работах [5, 6], в которых введены в рассмотрение соответственно Ω-расслоенные и ω-веерные формации. Одним из видов Ω-расслоенных формаций являются упомянутые ранее Ω-композиционные формации, а одним из важных видов ω-веерных формаций являются ω-центральные формации. Ввиду теоремы о соответствии ([7], теорема 4) между определенными видами ω-веерных и Ω-расслоенных формаций существует взаимосвязь. Так, например, согласно теореме о соответствии для каждой ω-центральной формации существует совпадающая с ней Ω-композиционная формация.
В настоящей работе изучаются τ-замкнутые ω-центральные и τ-замкнутые Ω-композиционные формации конечных групп, где τ — подгрупповой функтор, в частности, установлена взаимосвязь между минимальным τ-замкнутым ω-спутником ω-центральной формации и минимальным τ-замкнутым Ω-спутником Ω-композиционной формации; для произвольной непустой неединичной τ-замкнутой формации ![]() построены Ω-композиционная и ω-центральная формации, содержащие
построены Ω-композиционная и ω-центральная формации, содержащие ![]() .
.
Используемые обозначения и определения можно найти в [2–9]. Приведем лишь некоторые из них. Пусть ![]() — класс всех конечных групп;
— класс всех конечных групп; ![]() — класс всех конечных абелевых групп;
— класс всех конечных абелевых групп; ![]() — класс всех конечных простых групп; Ω — непустой подкласс класса
— класс всех конечных простых групп; Ω — непустой подкласс класса ![]() . Через
. Через ![]() обозначается класс всех простых групп, изоморфных композиционным факторам группы
обозначается класс всех простых групп, изоморфных композиционным факторам группы ![]() ;
; ![]() — объединение классов
— объединение классов ![]() для всех
для всех ![]() , где
, где ![]() — класс групп. Через
— класс групп. Через ![]() обозначается класс всех Ω-групп, т. е. таких групп
обозначается класс всех Ω-групп, т. е. таких групп ![]() , для которых
, для которых ![]() . Пусть
. Пусть ![]() . Тогда
. Тогда ![]() ;
; ![]() ,
, ![]() — класс всех групп, у которых каждый главный A-фактор централен. Функции
— класс всех групп, у которых каждый главный A-фактор централен. Функции ![]() {формации групп}, где
{формации групп}, где ![]() ;
; ![]() {формации групп};
{формации групп}; ![]() {непустые формации Фиттинга}, принимающие одинаковые значения на изоморфных группах из области определения, называются соответственно ΩF-функцией; F-функцией; FR-функцией [5, с. 126]. Формация
{непустые формации Фиттинга}, принимающие одинаковые значения на изоморфных группах из области определения, называются соответственно ΩF-функцией; F-функцией; FR-функцией [5, с. 126]. Формация ![]() и
и ![]() для всех
для всех ![]() называется Ω-расслоенной формацией с Ω-спутником
называется Ω-расслоенной формацией с Ω-спутником ![]() и направлением
и направлением ![]() ; формация
; формация ![]() для всех
для всех ![]() называется расслоенной формацией со спутником
называется расслоенной формацией со спутником ![]() и направлением
и направлением ![]() [5, с. 127]. Формация
[5, с. 127]. Формация ![]() (соответственно
(соответственно ![]() ) называется Ω-композиционной (композиционной), где
) называется Ω-композиционной (композиционной), где ![]() для всех
для всех ![]() [5, с. 128]. Направление φ Ω-расслоенной формации называется b-направлением, если
[5, с. 128]. Направление φ Ω-расслоенной формации называется b-направлением, если ![]() для любой абелевой группы
для любой абелевой группы ![]() ; r-направлением, если
; r-направлением, если ![]() для всех
для всех ![]() [8, с. 218].
[8, с. 218].
Пусть ![]() — множество всех простых чисел;
— множество всех простых чисел; ![]() — класс всех конечных p-групп, где
— класс всех конечных p-групп, где ![]() ; ω — непустое подмножество множества
; ω — непустое подмножество множества ![]() . Через
. Через ![]() обозначается класс всех ω-групп, т. е. таких групп
обозначается класс всех ω-групп, т. е. таких групп ![]() , для которых
, для которых ![]() ;
; ![]() — класс всех групп, у которых каждый главный p-фактор централен. Функции
— класс всех групп, у которых каждый главный p-фактор централен. Функции ![]() {формации групп}, где
{формации групп}, где ![]() ;
; ![]() {формации групп};
{формации групп}; ![]() {непустые формации Фиттинга} называются соответственно ωF-функцией;
{непустые формации Фиттинга} называются соответственно ωF-функцией; ![]() -функцией;
-функцией; ![]() -функцией [6, с. 44]. Формация
-функцией [6, с. 44]. Формация ![]() и
и ![]() для всех
для всех ![]() называется ω-веерной формацией с ω-спутником
называется ω-веерной формацией с ω-спутником ![]() и направлением
и направлением ![]() ; формация
; формация ![]() для всех
для всех ![]() называется веерной формацией со спутником
называется веерной формацией со спутником ![]() и направлением
и направлением ![]() [6, с. 45]. Формация
[6, с. 45]. Формация ![]() называется ω-центральной, где
называется ω-центральной, где ![]() для любого
для любого ![]() [7, с. 41]. Направление
[7, с. 41]. Направление ![]() ω-веерной формации называется b-направлением, если
ω-веерной формации называется b-направлением, если ![]() для любого
для любого ![]() ; p-направлением, если
; p-направлением, если ![]() для любого
для любого ![]() [7, с. 38].
[7, с. 38].
Пусть ![]() . Ω-спутник
. Ω-спутник ![]() Ω-расслоенной формации называется согласованным с ω-спутником
Ω-расслоенной формации называется согласованным с ω-спутником ![]() ω-веерной формации, если
ω-веерной формации, если ![]() для любого
для любого ![]() и
и ![]() . Направления
. Направления ![]() и
и ![]() соответственно ω-веерной и Ω-расслоенной формаций называются коллинеарными, если
соответственно ω-веерной и Ω-расслоенной формаций называются коллинеарными, если ![]() для любого
для любого ![]() ℙ [7, с. 42].
ℙ [7, с. 42].
Отображение ![]() , ставящее в соответствие каждой группе
, ставящее в соответствие каждой группе ![]() некоторую непустую систему
некоторую непустую систему ![]() ее подгрупп, называется подгрупповым функтором, если
ее подгрупп, называется подгрупповым функтором, если ![]() для любого изоморфизма
для любого изоморфизма ![]() группы
группы ![]() [9, с. 13]. Формация
[9, с. 13]. Формация ![]() называется τ-замкнутой, если
называется τ-замкнутой, если ![]() для любой группы
для любой группы ![]() [3, с. 23]. Ω-спутник (ω-спутник) Ω-расслоенной (ω-веерной) формации
[3, с. 23]. Ω-спутник (ω-спутник) Ω-расслоенной (ω-веерной) формации ![]() называется τ-замкнутым, если все его значения являются τ-замкнутыми формациями. Подгрупповой функтор
называется τ-замкнутым, если все его значения являются τ-замкнутыми формациями. Подгрупповой функтор ![]() называется регулярным, если выполняются следующие 2 условия:
называется регулярным, если выполняются следующие 2 условия:
1) если ![]() и N — нормальная подгруппа группы G, то
и N — нормальная подгруппа группы G, то ![]()
2) если ![]() , то
, то ![]() [9, с. 14].
[9, с. 14].
Подгрупповой функтор τ называется δ-радикальным, если для любой группы G и любой ![]() справедливо равенство
справедливо равенство ![]() для всех
для всех ![]() ℙ [10, с. 95]; Ω-радикальным, если для любой группы G и любой
ℙ [10, с. 95]; Ω-радикальным, если для любой группы G и любой ![]() справедливо равенство
справедливо равенство ![]() ; φ-радикальным, если для любой группы G и любой
; φ-радикальным, если для любой группы G и любой ![]() справедливо равенство
справедливо равенство ![]() для всех
для всех ![]() ; замкнутым относительно композиционных факторов, если для любой группы G и любой
; замкнутым относительно композиционных факторов, если для любой группы G и любой ![]() справедливо включение
справедливо включение ![]() [11, с. 76].
[11, с. 76].
Через ![]() обозначается τ-замкнутая Ω-расслоенная формация с направлением φ, порожденная множеством групп
обозначается τ-замкнутая Ω-расслоенная формация с направлением φ, порожденная множеством групп ![]() ,
, ![]() — Ω-расслоенная формация с направлением φ, обладающая хотя бы одним τ-замкнутым Ω-спутником, порожденная
— Ω-расслоенная формация с направлением φ, обладающая хотя бы одним τ-замкнутым Ω-спутником, порожденная ![]() [11, с. 77]. Через
[11, с. 77]. Через ![]() обозначается τ-замкнутая ω-веерная формация с направлением δ, порожденная множеством групп
обозначается τ-замкнутая ω-веерная формация с направлением δ, порожденная множеством групп ![]() ,
, ![]() — ω-веерная формация с направлением δ, обладающая хотя бы одним τ-замкнутым ω-спутником, порожденная
— ω-веерная формация с направлением δ, обладающая хотя бы одним τ-замкнутым ω-спутником, порожденная ![]() [10, с. 96].
[10, с. 96].
Приведем формулировки утверждений, используемых при доказательстве основных результатов статьи.
Лемма 1 (Лемма 2 [10]). Пусть ![]() — непустой класс групп, δ — такое направление ω-веерной формации, что
— непустой класс групп, δ — такое направление ω-веерной формации, что ![]() , и τ — регулярный подгрупповой функтор. Тогда формация
, и τ — регулярный подгрупповой функтор. Тогда формация ![]() имеет единственный минимальный τ-замкнутый ω-спутник
имеет единственный минимальный τ-замкнутый ω-спутник ![]() такой, что
такой, что
![]() ,
,
![]() для всех
для всех ![]() ,
,
![]() если
если ![]() .
.
Лемма 2 (Лемма 1 [10]). Пусть ![]() — ω-веерная формация с bp-направлением
— ω-веерная формация с bp-направлением ![]() ,
, ![]() , τ — регулярный ẟ-радикальный подгрупповой функтор. Формация
, τ — регулярный ẟ-радикальный подгрупповой функтор. Формация ![]() являетсяτ-замкнутой тогда и только тогда, когда
являетсяτ-замкнутой тогда и только тогда, когда ![]() обладает хотя бы одним τ-замкнутым ω-спутником.
обладает хотя бы одним τ-замкнутым ω-спутником.
Замечание 1. Если ![]() — непустой класс групп, ẟ —
— непустой класс групп, ẟ — ![]() -направление ω-веерной формации,
-направление ω-веерной формации, ![]() , τ — регулярный δ-радикальный подгрупповой функтор, то в силу леммы 2
, τ — регулярный δ-радикальный подгрупповой функтор, то в силу леммы 2 ![]() .
.
Лемма 3 (Лемма 3 [11]). Пусть ![]() — непустой класс групп,
— непустой класс групп, ![]() — такое направление Ω-расслоенной формации, что
— такое направление Ω-расслоенной формации, что ![]() , τ — регулярный подгрупповой функтор. Тогда формация
, τ — регулярный подгрупповой функтор. Тогда формация ![]() обладает единственным минимальным τ-замкнутым
обладает единственным минимальным τ-замкнутым ![]() -спутником
-спутником ![]() таким, что
таким, что
![]()
![]() для всех
для всех ![]()
![]() если
если ![]() ).
).
Лемма 4 (Лемма 2 [11]). Пусть ![]() — Ω-расслоенная формация с br-направлением φ,
— Ω-расслоенная формация с br-направлением φ, ![]() , τ — регулярный Ωφ-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов. Формация
, τ — регулярный Ωφ-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов. Формация ![]() является τ-замкнутой тогда и только тогда, когда
является τ-замкнутой тогда и только тогда, когда ![]() обладает хотя бы одним τ-замкнутым Ω-спутником.
обладает хотя бы одним τ-замкнутым Ω-спутником.
Замечание 2. Если ![]() — непустой класс групп,
— непустой класс групп, ![]() — br-направление Ω-расслоенной формации,
— br-направление Ω-расслоенной формации, ![]() и τ — регулярный Ωφ-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов, то в силу леммы 4
и τ — регулярный Ωφ-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов, то в силу леммы 4 ![]() .
.
Лемма 5 (Следствие 4.4 из теоремы 4 о соответствии [7]). Пусть ![]() — ω-центральная формация,
— ω-центральная формация, ![]() ,
, ![]() — Ω-композиционная формация с Ω-спутником
— Ω-композиционная формация с Ω-спутником ![]() согласованным с
согласованным с ![]() таким, что
таким, что ![]() для любого
для любого ![]() . Тогда
. Тогда ![]() .
.
Лемма 6 (Теорема 1 [12]). Пусть ![]() — непустая неединичная формация, Ω — непустой подкласс класса
— непустая неединичная формация, Ω — непустой подкласс класса ![]() ,
, ![]() — FR-функция,
— FR-функция, ![]() для любого
для любого ![]() . Тогда
. Тогда ![]() содержится в Ω-расслоенной формации
содержится в Ω-расслоенной формации ![]() , где
, где ![]() — такая Ω
— такая Ω![]() -функция, что
-функция, что ![]() для любого
для любого ![]() ,
, ![]() для любого
для любого ![]() , а для любого
, а для любого ![]() справедливо: если
справедливо: если ![]() , то
, то ![]() , если
, если ![]() , то
, то ![]() .
.
Лемма 7 (Теорема 2 [12]). Пусть ![]() — непустая неединичная формация,
— непустая неединичная формация, ![]() — p-направление ω-веерной формации,
— p-направление ω-веерной формации,![]() для любого
для любого ![]() . Тогда
. Тогда ![]() содержится в ω-веерной формации
содержится в ω-веерной формации ![]() , где
, где ![]() — такая
— такая ![]() -функция, что
-функция, что ![]()
![]() ,
, ![]() для любого
для любого ![]() , и для любого
, и для любого ![]() справедливо:
справедливо: ![]() , если
, если ![]() ,
, ![]() , если
, если ![]() .
.
Установим взаимосвязь между минимальным τ-замкнутым ω-спутником ω-центральной формации и минимальным τ-замкнутым Ω-спутником соответствующей ей Ω-композиционной формации.
Теорема 1. Пусть τ — регулярный ![]() -радикальный подгрупповой функтор,
-радикальный подгрупповой функтор, ![]() — ω-центральная формация с минимальным τ-замкнутым ω-спутником
— ω-центральная формация с минимальным τ-замкнутым ω-спутником ![]() ,
, ![]() ,
, ![]() — Ω-композиционная формация с минимальным τ-замкнутым Ω-спутником
— Ω-композиционная формация с минимальным τ-замкнутым Ω-спутником ![]() , обладающая Ω-спутником, согласованным с
, обладающая Ω-спутником, согласованным с ![]() . Тогда спутники
. Тогда спутники ![]() и
и ![]() также являются согласованными.
также являются согласованными.
Доказательство. Так как ![]() — τ-замкнутый ω-спутник формации
— τ-замкнутый ω-спутник формации ![]() , то согласно лемме 2 формация
, то согласно лемме 2 формация ![]() является τ-замкнутой. Поскольку
является τ-замкнутой. Поскольку ![]() — минимальный τ-замкнутый ω-спутник формации
— минимальный τ-замкнутый ω-спутник формации ![]() , то по лемме 1
, то по лемме 1 ![]() имеет следующее строение:
имеет следующее строение:
![]() (1);
(1);
![]() для всех
для всех ![]() (2);
(2);
![]() , если
, если ![]() (3).
(3).
Так как ![]() — минимальный τ-замкнутый Ω-спутник формации
— минимальный τ-замкнутый Ω-спутник формации ![]() , то по лемме 3
, то по лемме 3 ![]() имеет следующее строение:
имеет следующее строение:
![]() (4);
(4);
![]() для всех
для всех ![]() (5);
(5);
![]() , если
, если ![]() (6).
(6).
Пусть ![]() — Ω-спутник формации
— Ω-спутник формации ![]() , согласованный с ω-спутником
, согласованный с ω-спутником ![]() . Тогда по лемме 5
. Тогда по лемме 5 ![]() =
= ![]() . Так как
. Так как ![]() и
и ![]() согласованы, то по определению согласованных спутников
согласованы, то по определению согласованных спутников ![]() (7) и
(7) и ![]() (8) для любого
(8) для любого ![]() . Следовательно, Ω-спутник
. Следовательно, Ω-спутник ![]() формации
формации ![]() является τ-замкнутым. Установим, что спутники
является τ-замкнутым. Установим, что спутники ![]() и
и ![]() являются согласованными.
являются согласованными.
1) Покажем, что ![]() . Пусть
. Пусть ![]() . Установим, что
. Установим, что ![]() . Возьмем
. Возьмем ![]() . Проверим, что
. Проверим, что ![]() . Так как
. Так как ![]() , то
, то ![]() , где
, где ![]() . Поскольку
. Поскольку ![]() , имеем
, имеем ![]() , то есть
, то есть ![]() . Тогда
. Тогда 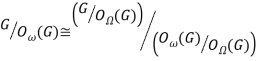 . Так как
. Так как ![]() , то по (4)
, то по (4) ![]() Поскольку
Поскольку ![]() — формация, то
— формация, то 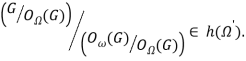 Таким образом,
Таким образом, ![]() , из чего следует, что
, из чего следует, что ![]() и
и ![]() . Поэтому
. Поэтому ![]() (9). Согласно лемме 1
(9). Согласно лемме 1 ![]() — единственный минимальный τ-замкнутый Ω-спутник формации
— единственный минимальный τ-замкнутый Ω-спутник формации ![]() . Это означает, что
. Это означает, что ![]() и, значит, ввиду (7)
и, значит, ввиду (7) ![]() (10). Из (9) и (10) делаем вывод, что
(10). Из (9) и (10) делаем вывод, что ![]() .
.
2) Покажем, что ![]() для всех
для всех ![]() . Пусть
. Пусть ![]() . Согласно строению спутника
. Согласно строению спутника ![]() справедливо
справедливо ![]() . Докажем, что
. Докажем, что ![]() . Для этого достаточно установить, что
. Для этого достаточно установить, что ![]() . Поскольку
. Поскольку ![]() и
и ![]() , то
, то ![]() . Проверим, что
. Проверим, что ![]() . Допустим, что
. Допустим, что ![]() . Тогда
. Тогда ![]() и
и ![]() . Получили противоречие. Это означает, что
. Получили противоречие. Это означает, что ![]() . Тогда
. Тогда ![]() . Поэтому ввиду (6)
. Поэтому ввиду (6) ![]() . Следовательно,
. Следовательно, ![]() .
.
Пусть ![]() . Поскольку направления
. Поскольку направления ![]() и
и ![]() являются коллинеарными, то из (2) и (5) имеем
являются коллинеарными, то из (2) и (5) имеем ![]() .
.
Из 1) и 2) делаем вывод, что ω-спутник ![]() формации
формации ![]() и
и ![]() -спутник
-спутник ![]() формации
формации ![]() являются согласованными. Теорема доказана.
являются согласованными. Теорема доказана.
В следующей теореме для произвольной непустой неединичной τ-замкнутой формации ![]() построим τ-замкнутую Ω-композиционную формацию, содержащую
построим τ-замкнутую Ω-композиционную формацию, содержащую ![]() .
.
Теорема 2. Пусть ![]() — регулярный
— регулярный ![]() -радикальный подгрупповой функтор, замкнутый относительно композиционных факторов,
-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов, ![]() — непустая неединичная τ-замкнутая формация, Ω — непустой подкласс класса
— непустая неединичная τ-замкнутая формация, Ω — непустой подкласс класса ![]() ,
, ![]() для любого
для любого ![]() . Тогда
. Тогда ![]() содержится в
содержится в ![]() -замкнутой Ω-композиционной формации
-замкнутой Ω-композиционной формации ![]() , где
, где ![]() — такая Ω
— такая Ω![]() -функция, что для любого
-функция, что для любого ![]() выполняется
выполняется ![]() , для любого
, для любого ![]() справедливо равенство
справедливо равенство ![]() , а для любого
, а для любого ![]() выполняется
выполняется ![]() , если
, если ![]() , и
, и ![]() , если
, если ![]() .
.
Доказательство. По лемме 6 ![]() содержится в Ω-композиционной формации
содержится в Ω-композиционной формации ![]() , где
, где ![]() — такая
— такая ![]() -функция, что для любого
-функция, что для любого ![]() справедливо
справедливо ![]() , для любого
, для любого ![]() выполняется
выполняется ![]() , а для любого
, а для любого ![]() выполняется
выполняется ![]() , если
, если ![]() , и
, и ![]() , если
, если ![]() .
.
Покажем, что![]() —
— ![]() -замкнутая формация. Для этого, ввиду леммы 4, достаточно проверить, что
-замкнутая формация. Для этого, ввиду леммы 4, достаточно проверить, что ![]() — τ-замкнутый Ω-спутник формации
— τ-замкнутый Ω-спутник формации ![]() . Пусть
. Пусть ![]() . Покажем, что
. Покажем, что ![]() — τ-замкнутая формация. Если
— τ-замкнутая формация. Если ![]() , то по условию
, то по условию ![]() и, значит,
и, значит, ![]() — τ-замкнутая формация. Пусть
— τ-замкнутая формация. Пусть ![]() . Тогда по условию
. Тогда по условию ![]() и в силу τ-замкнутости
и в силу τ-замкнутости ![]() получаем, что
получаем, что ![]() — τ-замкнутая формация.
— τ-замкнутая формация.
Пусть ![]() . Если
. Если ![]() , то по условию
, то по условию ![]() . Следовательно,
. Следовательно, ![]() — τ-замкнутая формация. Пусть
— τ-замкнутая формация. Пусть ![]() . Тогда по условию
. Тогда по условию ![]() . Покажем, что
. Покажем, что ![]() —
— ![]() -замкнутая формация. Возьмем
-замкнутая формация. Возьмем ![]() и
и ![]() . Установим, что
. Установим, что ![]() . Поскольку
. Поскольку ![]() и
и ![]() — подгрупповой функтор, замкнутый относительно композиционных факторов, то
— подгрупповой функтор, замкнутый относительно композиционных факторов, то ![]() . Так как
. Так как ![]() , то
, то ![]() и, значит,
и, значит, ![]() . Следовательно,
. Следовательно, ![]() и
и ![]() — τ-замкнутая формация. Поэтому
— τ-замкнутая формация. Поэтому ![]() — τ-замкнутая формация. Таким образом, что
— τ-замкнутая формация. Таким образом, что ![]() — τ-замкнутый Ω-спутник формации
— τ-замкнутый Ω-спутник формации ![]() . Тогда по лемме 4
. Тогда по лемме 4 ![]() — τ-замкнутая формация. Теорема доказана.
— τ-замкнутая формация. Теорема доказана.
В следующей теореме для произвольной непустой неединичной τ-замкнутой формации ![]() построим τ-замкнутую ω-центральную формацию, содержащую
построим τ-замкнутую ω-центральную формацию, содержащую ![]() .
.
Теорема 3. Пусть ![]() — непустая неединичная τ-замкнутая формация,τ — регулярный
— непустая неединичная τ-замкнутая формация,τ — регулярный ![]() -радикальный подгрупповой функтор,
-радикальный подгрупповой функтор, ![]() для любого
для любого ![]() . Тогда
. Тогда ![]() содержится в τ-замкнутой ω-центральной формации
содержится в τ-замкнутой ω-центральной формации ![]() , где
, где ![]() — такая
— такая ![]() -функция, что
-функция, что ![]() ,
, ![]() для любого
для любого ![]() , идля любого
, идля любого ![]() выполняется
выполняется ![]() , если
, если ![]() , и
, и ![]() , если
, если ![]() .
.
Доказательство. По лемме 7 ![]() содержится в ω-центральной формации
содержится в ω-центральной формации ![]() , где
, где ![]() — такая
— такая ![]() -функция, что
-функция, что ![]() ,
, ![]() для любого
для любого ![]() , и для любого
, и для любого ![]() выполняется
выполняется ![]() , если
, если ![]() , и
, и ![]() , если
, если ![]() .
.
Покажем, что ![]() — τ-замкнутая формация. Для этого, ввиду леммы 2, достаточно показать, что
— τ-замкнутая формация. Для этого, ввиду леммы 2, достаточно показать, что ![]() — τ-замкнутый ω-спутник формации
— τ-замкнутый ω-спутник формации ![]() . По условию
. По условию ![]() . Следовательно,
. Следовательно, ![]() — τ-замкнутая формация. Пусть
— τ-замкнутая формация. Пусть ![]() . Если
. Если ![]() , то по условию
, то по условию ![]() — τ-замкнутая формация. Пусть
— τ-замкнутая формация. Пусть ![]() . Если
. Если ![]() , то по условию
, то по условию ![]() и, значит,
и, значит, ![]() — τ-замкнутая формация. Пусть
— τ-замкнутая формация. Пусть ![]() . Покажем, что
. Покажем, что ![]() — τ-замкнутая формация. Пусть
— τ-замкнутая формация. Пусть ![]() и
и ![]() . Установим, что
. Установим, что ![]() . Так как
. Так как ![]() , то
, то ![]() . Это означает, что
. Это означает, что ![]() —
— ![]() -число и поэтому
-число и поэтому ![]() —
— ![]() -число. Таким образом,
-число. Таким образом, ![]() . Тогда
. Тогда ![]() и
и ![]() –
– ![]() -замкнутая формация. Следовательно, и в этом случае
-замкнутая формация. Следовательно, и в этом случае ![]() — τ-замкнутая формация.
— τ-замкнутая формация.
Тем самым установлено, что ![]() — τ-замкнутый ω-спутник формации
— τ-замкнутый ω-спутник формации ![]() . По лемме 2 получаем, что
. По лемме 2 получаем, что ![]() — τ-замкнутая формация. Теорема доказана.
— τ-замкнутая формация. Теорема доказана.
Литература:
1. Gaschütz W. Zur Theorie der endlichen auflösbaren Gruppen. — Math. Z., 1963. Vol. 80. № 4. — S. 300–305.
2. Шеметков Л. А. Формации конечных групп. — М.: Наука, 1978. — 272 с.
3. Скиба А. Н. Алгебра формаций. — Минск: Беларуская навука, 1997. — 240 с.
4. Doerk K., Нawkes T. Finite soluble groups. Walter de Gruyter, Berlin — New Jork, 1992. — 891 p.
5. Ведерников В. А., Сорокина М. М. Ω-расслоенные формации и классы Фиттинга конечных групп // Дискретная математика, 2001. Т. 13. Вып. 3. — С. 125–144.
6. Ведерников В. А., Сорокина М. М. ω-веерные формации и классы Фиттинга конечных групп // Математические заметки, 2002. Т. 71. № 1. — С. 43–60.
7. Ведерников В. А. О новых типах ω-веерных формаций конечных групп // Украiнський математичный конгресс — 2001. Секцiя 1. Працi. Киiв, 2002. — С. 36–45.
8. Vedernikov V. A. Maximal satellites of Ω-foliated formations and Fitting classes // Proc. Steklov Inst. Math., 2001. № 2. — P. 217–233.
9. Каморников С. Ф., Селькин М. В. Подгрупповые функторы и классы конечных групп. — Минск: Беларуская навука, 2003. — 254 с.
10. Корпачева М. А., Сорокина М. М. Критические ω-веерные τ-замкнутые формации конечных групп // Дискретная математика, 2011. Т. 23. Вып. 1. — С. 94–101.
11. Сорокина М. М., Корпачева М. А. Критические Ω-расслоенные τ-замкнутые формации конечных групп // Вестник Брянского государственного университета: Точные и естественные науки, 2012. № 4. — С. 75–79.
12. Сорокина М. М., Корочкина Г. О., Кочергина А. Н. О вложении классов конечных групп в Ω-расслоенные формации // Естественные и математические науки в современном мире: сб. ст. по матер. XLIX междунар. науч.-практ. конф. № 12 (47). — Новосибирск: СибАК, 2016. — С. 96–102.

